Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aron, Eleanor R
and
Hager, Anthony W
1981.
Convex vector lattices and l-algebras.
Topology and its Applications,
Vol. 12,
Issue. 1,
p.
1.
Kopytov, V. M.
1983.
Ordered groups.
Journal of Soviet Mathematics,
Vol. 23,
Issue. 6,
p.
2627.
Henriksen, Melvin
1989.
Ordered Algebraic Structures.
p.
143.
Henriksen, Melvin
1997.
Ordered Algebraic Structures.
p.
1.
Hager, Anthony W.
and
Martinez, Jorge
2002.
Functorial rings of quotients—III: the maximum in archimedean f-rings.
Journal of Pure and Applied Algebra,
Vol. 169,
Issue. 1,
p.
51.
Hager, Anthony W.
and
Martinez, Jorge
2002.
C-epic compactifications.
Topology and its Applications,
Vol. 117,
Issue. 2,
p.
113.
Boulabiar, Karim
2004.
Representation Theorems ford-Multiplications on Archimedean Unitalf-Rings.
Communications in Algebra,
Vol. 32,
Issue. 10,
p.
3955.
Ball, R. N.
Hager, A. W.
Johnson, D. G.
and
Kizanis, A.
2009.
A theorem and a question about epicomplete archimedean lattice-ordered groups.
Algebra universalis,
Vol. 62,
Issue. 2-3,
p.
165.
Boulabiar, Karim
and
Jabeur, Jamel
2010.
Arens regularity of lattice-ordered rings.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 19,
Issue. S1,
p.
25.
Boulabiar, Karim
and
Brahmi, Wael
2014.
Orthoproducts and f-representations of archimedean $${\ell}$$ ℓ -groups.
Algebra universalis,
Vol. 72,
Issue. 1,
p.
81.
Hager, Anthony
2015.
Some unusual epicomplete Archimedean lattice-ordered groups.
Proceedings of the American Mathematical Society,
Vol. 143,
Issue. 5,
p.
1969.
Lapenta, S.
and
Leuştean, I.
2016.
Stochastic independence for probability MV-algebras.
Fuzzy Sets and Systems,
Vol. 298,
Issue. ,
p.
194.
Hajji, Rawaa
2022.
Idempotent identities in f-rings.
Algebra universalis,
Vol. 83,
Issue. 4,
Stennder, Janko
2025.
Multimorphisms on pre-Riesz spaces of continuous functions.
Journal of Mathematical Analysis and Applications,
Vol. 541,
Issue. 2,
p.
128728.
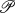 (S) of polar preserving endomorphisms of the l-group S. In fact, each f-multiplication of S is determined by a homomorphism of S+ into
(S) of polar preserving endomorphisms of the l-group S. In fact, each f-multiplication of S is determined by a homomorphism of S+ into 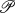 (S)+.
(S)+.

