Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T02:19:45.696Z Has data issue: false hasContentIssue false
  • English
  • Français

Action convergence of operators and graphs

Part of: Graph theory

Published online by Cambridge University Press:  17 September 2020

Ágnes Backhausz  and
Balázs Szegedy
Ágnes Backhausz*
Affiliation:
Department of Probability Theory and Statistics, ELTE Eötvös Loránd University, Budapest, Hungary and Alfréd Rényi Institute of Mathematics, Pázmány Péter sétány 1/c, H-1117Budapest, Hungary
Balázs Szegedy
Affiliation:
Alfréd Rényi Institute of Mathematics, Reáltanoda utca 13–15, H-1053Budapest, Hungary e-mail: [email protected]
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a new approach to graph limit theory that unifies and generalizes the two most well-developed directions, namely dense graph limits (even the more general 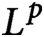$L^p$ limits) and Benjamini–Schramm limits (even in the stronger local-global setting). We illustrate by examples that this new framework provides a rich limit theory with natural limit objects for graphs of intermediate density. Moreover, it provides a limit theory for bounded operators (called P-operators) of the form 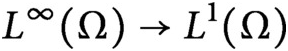$L^\infty (\Omega )\to L^1(\Omega )$ for probability spaces 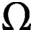$\Omega $ . We introduce a metric to compare P-operators (for example, finite matrices) even if they act on different spaces. We prove a compactness result, which implies that, in appropriate norms, limits of uniformly bounded P-operators can again be represented by P-operators. We show that limits of operators, representing graphs, are self-adjoint, positivity-preserving P-operators called graphops. Graphons, 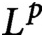$L^p$ graphons, and graphings (known from graph limit theory) are special examples of graphops. We describe a new point of view on random matrix theory using our operator limit framework.

Keywords

Graph limitsoperatorrandom matrix

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 1 , February 2022 , pp. 72 - 121
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

Footnotes

The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement n°617747. The research was partially supported by the MTA Rényi Institute Lendület Limits of Structures Research Group, and partially by the Mathematical Foundations of Artificial Intelligence project of the National Excellence Programme (grant no. 2018-1.2.1-NKP-2018-00008). A. B. was supported by the “Bolyai Ösztöndíj” of the Hungarian Academy of Sciences.

References

Backhausz, Á. and Szegedy, B., On large girth regular graphs and random processes on trees. Random Struct. Algor. 53(2018), no. 3, 389–416. http://org/10.1002/rsa.20769 CrossRefGoogle Scholar
Backhausz, Á. and Szegedy, B., On the almost eigenvectors of random regular graphs. Ann. Probab. 47(2019), no. 3, 1677–1725. http://org/10.1214/18-AOP1294 Google Scholar
Benjamini, I. and Curien, N., Ergodic theory on stationary random graphs. Electron. J. Probab. 17(2012), no. 93, 20 pp. http://org/10.1214/EJP.v17-2401 CrossRefGoogle Scholar
Benjamini, I. and Schramm, O., Recurrence of distributional limits of finite planar graphs. Electron. J. Probab. 6(2001), no. 23, 1–13. http://org/10.1214/EJP.v6-96 CrossRefGoogle Scholar
Berger, N., Borgs, C., Chayes, J. T., and Saberi, A., Asymptotic behavior and distributional limits of preferential attachment graphs. Ann. Probab. 42(2014), no. 1, 1–40. http://org/10.1214/12-AOP755 CrossRefGoogle Scholar
Borgs, C., Chayes, J. T., Cohn, H., and Holden, N., Sparse exchangeable graphs and their limits via graphon processes. J. Mach. Learn. Res. 18(2018), 1–71.Google Scholar
Borgs, C., Chayes, J. T., Cohn, H., and Zhao, Y., An ${L}^p$ theory of sparse graph convergence I: limits, sparse random graph models, and power law distributions. Trans. Am. Math. Soc. 372(2019), no. 5, 3019–3062. http://org/10.1090/tran/7543 CrossRefGoogle Scholar
Borgs, C., Chayes, J. T., Cohn, H., and Zhao, Y., An ${L}^p$ theory of sparse graph convergence II: LD convergence, quotients, and right convergence. Ann. Probab. 46(2018), no. 1, 337–396. http://org/10.1214/17-AOP1187 CrossRefGoogle Scholar
Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T., and Vesztergombi, K., Convergent sequences of dense graphs. I. Subgraph frequencies, metric properties and testing. Adv. Math. 219(2008), no. 6, 1801–1851. http://org/10.1016/j.aim.2008.07.008 CrossRefGoogle Scholar
Borgs, C., Chayes, J., and Lovász, L., Moments of two-variable functions and the uniqueness of graph limits. Geom. Funct. Anal. 19(2010), no. 6, 1597–1619. http://org/10.1007/s00039-010-0044-0 CrossRefGoogle Scholar
Bollobás, B. and Riordan, O., Sparse graphs: metrics and random models. Random Struct. Algorithms 39(2011), 1–38. http://org/10.1002/rsa.20334 CrossRefGoogle Scholar
Candela, P. and Szegedy, B., Nilspace factors for general uniformity seminorms, cubic exchangeability and limits. Preprint, 2018. http://arxiv.org/pdf/1803.08758.pdf Google Scholar
Driver, B. K., Analysis tools with examples. Lecture Notes, Springer, New York, NY, 2003. http://www.math.ucsd.edu/~bdriver/240A-C-03-04/LectureNotes/anal2p-new.pdf.Google Scholar
Elek, G., On the limit of large girth graph sequences. Combinatorica 30(2010), no. 5, 553–563. http://org/10.1007/s00493-010-2559-2 CrossRefGoogle Scholar
Elek, G. and Szabó, E., Sofic groups and direct finiteness. J. Algebra 280(2004), no. 2, 426–434. http://org/10.1016/j.jalgebra.2004.06.023 10.1016/j.jalgebra.2004.06.023CrossRefGoogle Scholar
Erdős, L., Knowles, A., Yau, H. T., and Yin, J., Spectral statistics of Erdős-Rényi graphs I: local semicircle law. Ann. Probab. 41(2013), no. 3B, 2279–2375. http://org/10.1214/11-AOP734 CrossRefGoogle Scholar
Fremlin, D. H., Measure theory. Vol. 4, Torres Fremlin, Colchester, 2006.Google Scholar
Frenkel, P. E., Convergence of graphs with intermediate density. Trans. Am. Math. Soc. 370(2018), no. 5, 3363–3404. http://org/10.1090/tran/7036 CrossRefGoogle Scholar
Geman, S., A limit theorem for the norm of random matrices. Ann. Probab. 8(1980), no. 2, 252–261.CrossRefGoogle Scholar
Gordon, R. A., Real analysis: A first course . Addison Wesley Higher Mathematics, Reading, MA, 1997.Google Scholar
Hatami, H., Lovász, L., and Szegedy, B., Limits of locally-globally convergent graph sequences. Geom. Funct. Anal. 24(2014), no. 1, 269–296. http://org/10.1007/s00039-014-0258-7 CrossRefGoogle Scholar
Hazelwinkel, M. (ed.), Encyclopaedia of mathematics. Vol. 4, Kluwer Academic Publishers, Dordrecht, The Netherlands, 1989. http://org/10.1007/978-94-009-6000-8 Google Scholar
Janson, S., Graphons and cut metric on $\sigma$ -finite measure spaces. Preprint, 2016. http://arxiv.org/pdf/1608.01833.pdf Google Scholar
Kun, G. and Thom, A., Inapproximability of actions and Kazhdan’s property (T). Preprint, 2019. https://arxiv.org/abs/1901.03963 Google Scholar
Kunszenti-Kovács, D., Lovász, L., and Szegedy, B., Multigraph limits, unbounded kernels, and Banach space decorated graphs. Preprint, 2014. arXiv:1406.7846 Google Scholar
Kunszenti-Kovács, D., Lovász, L., and Szegedy, B., Measures on the square as sparse graph limits. J. Combin. Theory Ser. B 138(2019), 1–40. http://org/10.1016/j.jctb.2019.01.004 CrossRefGoogle Scholar
Lovász, L., Large networks and graph limits . Amer. Math. Soc., 60, American Mathematical Society Colloquium Publications, Providence, RI, 2012.Google Scholar
Lovász, L. and Szegedy, B., Limits of dense graph sequences. J. Combin. Theory Ser. B 96(2006), no. 6, 933–957. http://org/10.1016/j.jctb.2006.05.002 CrossRefGoogle Scholar
Lovász, L. and Szegedy, B., Szemerédi’s lemma for the analyst. Geom. Funct. Anal. 17(2007), no. 1, 252–270. http://org/10.1007/s00039-007-0599-6 CrossRefGoogle Scholar
Lyons, R. and Peres, Y., Probability on trees and networks . Cambridge Series in Statistical and Probabilistic Mathematics, 42, Cambridge University Press, New York, NY, 2016. http://org/10.1017/9781316672815 CrossRefGoogle Scholar
Male, C. and Péché, S., Uniform regular weighted graphs with large degree: Wigner’s law, asymptotic freeness and graphons limit. Preprint, 2014. http://arxiv.org/pdf/1410.8126.pdf Google Scholar
Nešetřil, J. and Ossona de Mendez, P., Sparsity, algorithms and combinatorics. Vol. 28, Springer, Heidelberg, Germany, 2012. http://org/10.1007/978-3-642-27875-4 Google Scholar
Nešetřil, J. and Ossona de Mendez, P., Local-global convergence, an analytic and structural approach. Preprint, 2018. http://arxiv.org/pdf/1805.02051.pdf Google Scholar
Rudas, A., Tóth, B., and Valkó, B., Random trees and general branching processes. Random Struct. Algor. 31(2007), no. 2, 186–202. http://org/10.1002/rsa.20137 CrossRefGoogle Scholar
Szegedy, B., Sparse graph limits, entropy maximization and transitive graphs. Preprint, 2015. arXiv:1504.00858 Google Scholar
Szegedy, B., On the colored star metric. Manuscript in preparation.Google Scholar
Zhu, Y., A graphon approach to limiting spectral distributions of Wigner-type matrices. Random Struct. Algor. 56(2020), no. 1, 251–279. http://org/10.1002/rsa.20894 CrossRefGoogle Scholar