Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T02:36:21.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute Tauberian Constants for Hausdorff Transformations

Published online by Cambridge University Press:  20 November 2018

Soraya Sherif
Soraya Sherif*
Affiliation:
Education College for Women, Riyadhy Saudi Arabia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 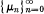be a fixed sequence of real or complex numbers. The Hausdorff transform {tn} of a sequence \sn) by means of the fixed sequence 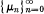(or, in short, the (H, μn) transform) is given by

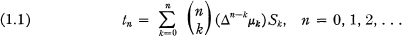
where, for r, q ≧ 0,

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 1 , February 1974 , pp. 19 - 26
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Bateman, H., Higher transcendental functions, Volume 1 (McGraw-Hill, New York, 1953).Google Scholar
2. Fekete, M., Vizsálatok az absolut summabilis sorokrol, alkalmazással a Direchlet —éss Fourier —sorokra, math, és Termés. Ért. 32 (1914), 389–425.Google Scholar
3. Hardy, G. H., Divergent series (Oxford Univ. Press, Oxford, 1940).Google Scholar
4. Hyslop, J. M., A Tauberian theorem for absolute summability, J. London Math. Soc. 12 (1937), 176–180.Google Scholar
5. Jakimovski, A., The sequence-to-function analogues to Hausdorff transformations, The Bull, of the Research Council of Israel. Vol. 8F, No. 3 (1960), 135–154.Google Scholar
6. Knopp, K. and Lorentz, G. G., Belträge Zür absoluten Limitierung. Arch. Math. (Basel) 2 (1949), 10–16.Google Scholar
7. Maddox, I. J., Elements of functional analysis (Cambridge Univ. Press, 1970).Google Scholar
8. Mears, F. M., Absolute regularity and the Norlund mean, Ann. of Math. 83 (1937), 594–601.Google Scholar
9. Sherif, S., Absolute Tauberian constants for Cesaro means, Trans. Amer. Math. Soc. 168 (1972), 233-241. Google Scholar
10. Whittaker, J.M., The absolute summability of Fourier series, Proc. Edinburgh Math. Soc. 2 (1931), 1–5.Google Scholar