Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-16T15:08:20.769Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute Convergence Factors for Hp Series

Published online by Cambridge University Press:  20 November 2018

James Caveny
James Caveny*
Affiliation:
Florida State University, Tallahassee, Florida
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

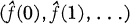A famous theorem of Hardy asserts that if f ∊ H1, then the sequence of Fourier coefficients satisfies 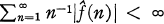. For this reason we say that the sequence (1, 1/2, 1/3, …) belongs to the multiplier class (H1, l1). In this paper, we investigate the multiplier classes (Hp, l1) for 1 ≧ p ≧ ∞. Our observations are based on the fact that a sequence (λ(0), λ(l), …) belongs to (Hp, l1) independent of the arguments of its terms. We also show that (Hp, l1) may be thought of as the conjugate space of a certain Banach space.

1. Preliminaries.Lp denotes the space of complex-valued Lebesgue measurable functions f defined on the circle |z| = 1 such that

is finite.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 187 - 195
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Caveny, D. J., Bounded Hadamard products of Hp functions, Duke Math. J. 88 (1966), 389–394.Google Scholar
2. Curtis, P. C., Jr. and Figà-Talamanca, A., Factorization theorems in Banach algebras; Function algebras (Proc. Internat. Sympos. on Function Algebras, Tulane Univ., 1965), pp. 169–185 (Scott Foresman, Chicago, 111., 1966).Google Scholar
3. Figà-Talamanca, A., Translation invariant operators in Lp, Duke Math. J. 82 (1965), 495–501.Google Scholar
4. Hoffman, K., Banach spaces of analytic functions (Prentice-Hall, Englewood Cliffs, N.J., 1962).Google Scholar
5. Piranian, G., Shields, A. L., and Wells, J. H., Bounded analytic functions and absolutely continuous measures, Proc. Amer. Math. Soc. 18 (1967), 818–826.Google Scholar
6. Wells, J. H., Some results concerning multipliers of HP (to appear).Google Scholar
7. Zygmund, A., Trigonometric Series, Vol. I, 2nd ed. (Cambridge Univ. Press, New York, 1959).Google Scholar