Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T03:10:01.513Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute Continuity of Wasserstein Barycenters Over Alexandrov Spaces

Published online by Cambridge University Press:  20 November 2018

Yin Jiang
Yin Jiang*
Affiliation:
Department of Mathematics, Sun Yat-sen University, Guangzhou, 510275, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we prove that on a compact, $n$-dimensional Alexandrov space with curvature at least −1, the Wasserstein barycenter of Borel probability measures 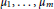${{\mu }_{1}},\ldots ,{{\mu }_{m}}$ is absolutely continuous with respect to the $n$-dimensional Hausdorff measure if one of them is.

Keywords

51K0549K30Alexandrov spaceWasserstein barycentermulti-marginal optimal transport
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 5 , 01 October 2017 , pp. 1087 - 1108
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Agueh, M. and Calier, G., Barycenters in the Wasserstein space. SIAM J. Math. Anal. 43(2011),no. 2, 904–924.http://dx.doi.Org/10.1137/100805741 Google Scholar
[2] Ambrosio, L. and Gigli, N., A user's guide to optimal transport. In: Modelling and optimisation of flows on networks, Lecture Notes in Math., 2062, Springer, Heidelberg, 2013,1–155.http://dx.doi.org/10.1007/978-3-642-32160-3J Google Scholar
[3] Ambrosio, L., Gigli, N., and Savaré, G., Gradient flows: in metric spaces and in the space of probability measures. Lectures in Mathematics ETH Zﺫurich, Birkhﺫauser Verlag, Basel, 2005.Google Scholar
[4] Bertrand, J., Existence and uniqueness of optimal maps on Alexandrov spaces. Adv. Math. 219(2008), no. 3, 838–851.http://dx.doi.org/10.1016/j.aim.2008.06.008 Google Scholar
[5] Burago, D., Burago, Y., and Ivanov, S., A course in metric geometry. Graduate Studies in Mathematics, 33, American Mathematical Society, Providence, RI, 2001.http://dx.doi.Org/10.1090/gsm/033 Google Scholar
[6] Burago, Y., Gromov, M., and Perel'man, G., A. D. Alexandrov spaces with curvature bounded below. Russian Math. Surveys 47(1992), no. 2,1–58. http://dx.doi.Org/10.1070/RM1992v047n02 ABEH000877 Google Scholar
[7] Carlier, G. and Ekeland, I., Matching for teams. Econom. Theory 42(2010), no. 2, 397–418.http://dx.doi.Org/10.1007/sOOI99-008-041 5-z Google Scholar
[8] Cheeger, J., Differentiability of Lipschitz functions on metric measure spaces. Geom. Funct. Anal. 9(1999), no. 3, 428–517. http://dx.doi.Org/10.1007/s000390050094 Google Scholar
[9] Cordero-Erausquin, D., McCann, R., and Schmuckenschläger, M., A Riemannian interpolation inequality á la Borel, Brascamp and Lieb. Invent. Math. 146(2001), 219–257.http://dx.doi.Org/10.1007/s00222O100160 Google Scholar
[10] Figalli, A. and Juillet, N., Absolute continuity of Wasserstein geodesies in the Heisenberggroup. J. Funct. Anal. 255(2008), 133–141.http://dx.doi.Org/10.1016/j.jfa.2008.03.006 Google Scholar
[11] Gangbo, W. and Swiech, A., Optimal maps for the multidimensional Monge-Kantorovich problem. Comm. Pure Appl. Math. 51(1998), 23–45.http://dx.doi.Org/10.1002/(SICI)1097-0312(199801)51:1 <23::AID-CPA2>3.0.CO;2-H 3.0.CO;2-H>Google Scholar
[12] Kellerer, H. G., Duality theorems for marginal problems. Z. Wahrsch. Verw. Gebiete 67(1984),399–432.http://dx.doi.org/10.1007/BF00532047 Google Scholar
[13] Kim, Y.-H. and Pass, B., Wasserstein barycenters over Riemannian manifolds. arxiv:1412.7726 Google Scholar
[14] Kim, Y.-H., Multi-marginal optimal transport on Riemannian manifolds. Amer. J. Math. 137(2015), 1045–1060.http://dx.doi.org/10.1353/ajm.2015.0024 Google Scholar
[15] McCann, R., A convexity principle for interacting gases and equilibrium crystals. Ph.D. thesis, Princeton University, 1994.Google Scholar
[16] McCann, R., Polar factorization of maps on Riemannian manifolds. Geom. Funct. Anal. 11(2001), 589–608.http://dx.doi.org/10.1007/PL00001679 Google Scholar
[17] Ohta, S., Barycenters in Alexandrov spaces of curvature bounded below. Adv. Geom. 12(2012), 571–587.Google Scholar
[18] Otsu, Y. and Shioya, T., The Riemannian structure of Alexandrov spaces. J. Diferential Geom. 39(1994), 629–658.Google Scholar
[19] Pass, B., Uniqueness and Monge solutions in the multimarginal optimal transportation problem. SIAM J. Math. Anal. 43(2011), no. 6. 2758–2775.http://dx.doi.Org/10.1137/100804917 Google Scholar
[20] Pass, B., Multi-marginal optimal transport and multi-agent matching problems: uniqueness and structure of solutions. Discrete Contin. Dyn. Syst. 34(2014), no. 4,1623–1639.http://dx.doi.Org/1O.3934/dcds.2O14.34.1 623 Google Scholar
[21] Pass, B., Optimal transportation with infinitely many marginals. J. Funct. Anal. 264(2013), no. 4, 947–963.http://dx.doi.0rg/IO.IOI6/j.jfa.2Oi2.i2.OO2 Google Scholar
[22] Perelman, G., Elements of Morse theory on Alexandrov spaces. St. Petersburg Math. J. 5(1994), 205–213.Google Scholar
[23] Perelman, G. and Petrunin, A., Quasigeodesics and gradient curves in Alexandrov spaces. http://www.math.psu.edu/petrunin/ Google Scholar
[24] Petrunin, A., Subharmonic functions on Alexandrov space, http://www.math.psu.edu/petrunin/ Google Scholar
[25] Petrunin, A., Parallel transportation for Alexandrov spaces with curvature bounded below. Geom. Funct. Anal. 8(1998), 123–148.http://dx.doi.Org/10.1007/s000390050050 Google Scholar
[26] Petrunin, A., Semiconcave functions in Alexandrov's geometry. Surv. Differ. Geom., 11, Int. Press, Somerville, MA, 2007, pp. 137–201.http://dx.doi.org/10.4310/SDC.2006.v11.n1.a6 Google Scholar
[27] Rachev, S. T. and Rüschendorf, L., Mass transportation problems. Vol. I. Probability and its Applications (New York), Springer-Verlag, New York, 1998, pp. 57–106.Google Scholar
[28] Villani, C., Topics in optimal transportation. Graduate Studies in Mathematics, 58, American Mathematical Society, Providence, RI, 2003.http://dx.doi.Org/10.1007/b12016 Google Scholar
[29] Zhang, H. C. and Zhu, X. P., Yau's gradient estimates on Alexandrov spaces. J. Diferential Geom. 91(2012), 445–522.Google Scholar