Article contents
Two problems on random analytic functions in Fock spaces
Published online by Cambridge University Press: 08 July 2022
Abstract
Let 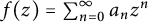 $f(z)=\sum _{n=0}^\infty a_n z^n$ be an entire function on the complex plane, and let
$f(z)=\sum _{n=0}^\infty a_n z^n$ be an entire function on the complex plane, and let 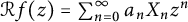 ${\mathcal R} f(z) = \sum _{n=0}^\infty a_n X_n z^n$ be its randomization induced by a standard sequence
${\mathcal R} f(z) = \sum _{n=0}^\infty a_n X_n z^n$ be its randomization induced by a standard sequence 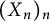 $(X_n)_n$ of independent Bernoulli, Steinhaus, or Gaussian random variables. In this paper, we characterize those functions
$(X_n)_n$ of independent Bernoulli, Steinhaus, or Gaussian random variables. In this paper, we characterize those functions 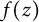 $f(z)$ such that
$f(z)$ such that 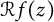 ${\mathcal R} f(z)$ is almost surely in the Fock space
${\mathcal R} f(z)$ is almost surely in the Fock space 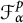 ${\mathcal F}_{\alpha }^p$ for any
${\mathcal F}_{\alpha }^p$ for any 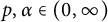 $p, \alpha \in (0,\infty )$. Then such a characterization, together with embedding theorems which are of independent interests, is used to obtain a Littlewood-type theorem, also known as regularity improvement under randomization within the scale of Fock spaces. Other results obtained in this paper include: (a) a characterization of random analytic functions in the mixed-norm space
$p, \alpha \in (0,\infty )$. Then such a characterization, together with embedding theorems which are of independent interests, is used to obtain a Littlewood-type theorem, also known as regularity improvement under randomization within the scale of Fock spaces. Other results obtained in this paper include: (a) a characterization of random analytic functions in the mixed-norm space 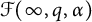 ${\mathcal F}(\infty , q, \alpha )$, an endpoint version of Fock spaces, via entropy integrals; (b) a complete description of random lacunary elements in Fock spaces; and (c) a complete description of random multipliers between different Fock spaces.
${\mathcal F}(\infty , q, \alpha )$, an endpoint version of Fock spaces, via entropy integrals; (b) a complete description of random lacunary elements in Fock spaces; and (c) a complete description of random multipliers between different Fock spaces.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
X. Fang is supported by MOST of Taiwan (108-2628-M-008-003-MY4).
References
- 4
- Cited by



