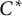Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T14:38:12.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Tracial approximation in simple ${C}^{\ast }$-algebras

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  26 February 2021

Xuanlong Fu  and
Huaxin Lin
Xuanlong Fu*
Affiliation:
Shanghai Center for Mathematical Sciences, Fudan University, Shanghai200438, China
Huaxin Lin
Affiliation:
Department of Mathematics, East China Normal University, Shanghai, China and (Current) Department of Mathematics, University of Oregon, Eugene, OR97403, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

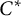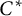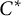We revisit the notion of tracial approximation for unital simple $C^*$ -algebras. We show that a unital simple separable infinite dimensional $C^*$ -algebra A is asymptotically tracially in the class of $C^*$ -algebras with finite nuclear dimension if and only if A is asymptotically tracially in the class of nuclear 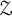$\mathcal {Z}$ -stable 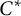$C^*$ -algebras.

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L35: Classifications of $C^*$-algebras
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 4 , August 2022 , pp. 942 - 1004
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Huaxin Lin is the corresponding author.

Xuanlong Fu was supported by China Postdoctoral Science Foundation, grant # 2020M670962, and partially supported by an NSFC grant (NSFC 11420101001). Huaxin Lin was partially supported by an NSF grant (DMS-1954600). Both authors acknowledge the support from the Research Center of Operator Algebras at East China Normal University which is partially supported by Shanghai Key Laboratory of PMMP, Science and Technology Commission of Shanghai Municipality (STCSM), grant #13dz2260400 and a NNSF grant (11531003).

References

Blackadar, B. and Handelman, D., Dimension functions and traces on C*-algebra. J. Funct. Anal. 45(1982), 297–340.CrossRefGoogle Scholar
Blackadar, B. and Kirchberg, E., Generalized inductive limits of finite-dimensional C*-algebras. Math. Ann. 307(1997), no. 3, 343–380.CrossRefGoogle Scholar
Blanchard, E. and Kirchberg, E., Non-simple purely infinite ${C}^{\ast }$ -algebras: the Hausdorff case . J. Funct. Anal. 207(2004), no. 2, 461–513.CrossRefGoogle Scholar
Bosa, J., Brown, N., Sato, Y., Tikuisis, A., White, S., and Winter, W., Covering dimension of ${C}^{\ast }$ -algebras and 2-coloured classification . Mem. Amer. Math. Soc. 257(2019), no. 1233, vii+97 pp.Google Scholar
Bosa, J., Gabe, J., Sims, A., and White, S., The nuclear dimension of ${\mathbf{\mathcal{O}}}_{\infty }$ -stable ${C}^{\ast }$ -algebras. Preprint, 2019. arXiv:1906.02066v1 Google Scholar
Brown, L. and Pedersen, G., On the geometry of the unit ball of a ${C}^{\ast }$ -algebra . J. Reine Angew. Math. 469(1995), 113–147.Google Scholar
Brown, N. P. and Ozawa, N., ${C}^{\ast }$ -algebras and finite-dimensional approximations. Graduate Studies in Mathematics, 88, American Mathematical Society, Providence, RI, 2008. xvi+509 pp.CrossRefGoogle Scholar
Castillejos, J., Evington, S., Tikuisis, A., White, S., and Winter, W., Nuclear dimension of simple ${C}^{\ast }$ -algebras , Invent. Math. 224(2020), no. 1, 245–290.CrossRefGoogle Scholar
Choi, M. and Effros, E., The completely positive lifting problem for ${C}^{\ast }$ -algebras . Ann. Math. 104(1976), no. 3, 585–609.CrossRefGoogle Scholar
Cuntz, J., Dimension functions on simple ${C}^{\ast }$ -algebras . Math. Ann. 233(1978), no. 2, 145–153.CrossRefGoogle Scholar
Cuntz, J., $K$ -theory for certain ${C}^{\ast }$ -algebras . Ann. Math. 113(1981), no. 1, 181–197.CrossRefGoogle Scholar
Dădărlat, M., Nonnuclear subalgebras of AF algebras . Amer. J. Math 122(2000), no.3, 581–597.CrossRefGoogle Scholar
Eilers, S., Loring, T., and Pedersen, G. K., Stability of anticommutation relations: an application of noncommutative CW complexes . J. Reine Angew. Math. 499(1998), 101–143.Google Scholar
Elliott, G., The classification problem for amenable ${C}^{\ast }$ -algebras. Proceedings of the International Congress of Mathematicians, 1, 2 (Zürich, 1994), Birkhäuser, Basel, 1995, pp. 922–932.CrossRefGoogle Scholar
Elliott, G. and Gong, G., On the classification of ${C}^{\ast }$ -algebras of real rank zero, II . Ann. Math. 144(1996), no. 2, 497–610.CrossRefGoogle Scholar
Elliott, G., Gong, G., and Li, L., On the classification of simple inductive limit ${C}^{\ast }$ -algebras II: the isomorphism theorem . Invent. Math. 168(2007), 249–320.CrossRefGoogle Scholar
Elliott, G., Gong, G., Lin, H., and Niu, Z., On the classification of simple amenable ${C}^{\ast }$ -algebras with finite decomposition rank, II. Preprint, 2016. arXiv:1507.03437 CrossRefGoogle Scholar
Elliott, G. and Niu, Z., On tracial approximation . J. Funct. Anal. 254(2008), no. 2, 396–440.CrossRefGoogle Scholar
Fan, Q. and Fang, X., C*-algebras of tracially stable rank one . Acta Math. Sin. (Chin. Ser.) 48(2005), no. 5, 929–934. In Chinese.Google Scholar
Fu, X., Simple generalized inductive limits of ${C}^{\ast }$ -algebras . Sci. China Math. 64(2021), no. 5, 1029–1044.CrossRefGoogle Scholar
Gong, G., Lin, H., and Niu, Z., A classification of finite simple amenable $\mathbf{\mathcal{Z}}$ -stable ${C}^{\ast }$ -algebras, I: ${C}^{\ast }$ -algebras with generalized tracial rank one . C. R. Math. Rep. Acad. Sci. Canada 42(2020), 63–450.Google Scholar
Gong, G., Lin, H., and Niu, Z., A classification of finite simple amenable $\mathbf{\mathcal{Z}}$ -stable ${C}^{\ast }$ -algebras, II: ${C}^{\ast }$ -algebras with rational generalized tracial rank one . C. R. Math. Rep. Acad. Sci. Canada 42(2020), 451–539.Google Scholar
Jiang, X. and Su, H., On a simple unital projectionless ${C}^{\ast }$ -algebras . Amer. J. Math. 121(1999), no. 2, 359–413.Google Scholar
Kadison, R., A generalized Schwarz inequality and algebraic invariants for operator algebras . Ann. Math. Second Ser. 56(1952), no. 3, 494–503.CrossRefGoogle Scholar
Kirchberg, E. and Phillips, N. C., Embedding of exact ${C}^{\ast }$ -algebras in the Cuntz algebra ${\mathbf{\mathcal{O}}}_2.$ J. Reine Angew. Math. 525(2000), 17–53.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M., Non-simple purely infinite C*-algebras. Amer. J. Math. 122(2000), no. 3, 637–666.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M., Infinite non-simple ${C}^{\ast }$ -algebras: absorbing the Cuntz algebras ${\mathbf{\mathcal{O}}}_{\infty }$ , (English summary). Adv. Math. 167(2002), no. 2, 195–264.CrossRefGoogle Scholar
Kirchberg, E. and Winter, W., Covering dimension and quasidiagonality . Int. J. Math. 15(2004), no. 1, 63–85.CrossRefGoogle Scholar
Lee, H. and Osaka, H., Tracially sequentially-split ${}^{\ast }$ -homomorphisms between C-algebras II. Preprint, 2017. arXiv:1906.06950v1 Google Scholar
Lin, H., Simple ${C}^{\ast }$ -algebras with continuous scales and simple corona algebras . Proc. Amer. Math. Soc. 112(1991), 871–880.Google Scholar
Lin, H., An introduction to the classification of amenable C*-algebras. World Scientific Publishing Co. Inc, River Edge, NJ, 2001, xii+320 pp.Google Scholar
Lin, H., Tracially AF ${C}^{\ast }$ -algebras . Trans. Amer. Math. Soc. 353(2001), 693–722.CrossRefGoogle Scholar
Lin, H., The tracial topological rank of ${C}^{\ast }$ -algebras . Proc. Lond. Math. Soc. 83(2001), 199–234.CrossRefGoogle Scholar
Lin, H., Classification of simple ${C}^{\ast }$ -algebras of tracial topological rank zero . Duke Math. J. 125(2004), no. 1, 91–119.CrossRefGoogle Scholar
Lin, H., Simple nuclear ${C}^{\ast }$ -algebras of tracial topological rank one . J. Funct. Anal. 251(2007), no. 2, 601–679.CrossRefGoogle Scholar
Lin, H., Asymptotic unitary equivalence and classification of simple amenable ${C}^{\ast }$ -algebras . Invent. Math. 183(2011), no. 2, 385–450.CrossRefGoogle Scholar
Lin, H., Localizing the Elliott conjecture at strongly self-absorbing ${C}^{\ast }$ -algebras, II . J. Reine Angew. Math. 692(2014), 233–243.Google Scholar
Lin, H., Locally AH algebras . Mem. Amer. Math. Soc. 235(2015), no. 1107, vi+109 pp.Google Scholar
Lin, H. and Niu, Z., Lifting $\mathrm{KK}$ -elements, asymptotic unitary equivalence and classification of simple ${C}^{\ast }$ -algebras . Adv. Math. 219(2008), no. 5, 1729–1769.CrossRefGoogle Scholar
Lin, H. and Zhang, S., On infinite simple ${C}^{\ast }$ -algebras. J. Funct. Anal. 100(1991), no. 1, 221–231.CrossRefGoogle Scholar
Matui, H. and Sato, Y., Strict comparison and $\mathbf{\mathcal{Z}}$ -absorption of nuclear ${C}^{\ast }$ -algebras . Acta Math. 209(2012), no. 1, 179–196.CrossRefGoogle Scholar
Matui, H. and Sato, Y., Decomposition rank of UHF-absorbing ${C}^{\ast }$ -algebras . Duke Math. J. 163(2014), no. 14, 2687–2708.CrossRefGoogle Scholar
Niu, Z. and Wang, Q., With an appendix by Eckhardt, A tracially AF algebra which is not $\mathbf{\mathcal{Z}}$ -absorbing. Preprint, 2019. arXiv:1902.03325v2 Google Scholar
Ortega, E., Perera, F., and Rørdam, M., The corona factorization property, stability, and the Cuntz semigroup of a ${C}^{\ast }$ -algebras . Int. Math. Res. Not. IMRN (2012), 34–66 CrossRefGoogle Scholar
Rørdam, M., On the structure of simple ${C}^{\ast }$ -algebras tensored with a UHF-algebra . J. Funct. Anal. 100(1991), 1–17.CrossRefGoogle Scholar
Rørdam, M., On the structure of simple ${C}^{\ast }$ -algebras tensored with a UHF-algebra. II . J. Funct. Anal. 107(1992), 255–269.CrossRefGoogle Scholar
Rørdam, M., Classification of nuclear, simple C*-algebras. Classification of nuclear C*-algebras. Entropy in operator algebras. Encyclopaedia Math. Sci. 126, Oper. Alg. Non-Commut. Geom., 7, Springer, Berlin, Germany, 2002, pp. 1–145.CrossRefGoogle Scholar
Rørdam, M., The stable and the real rank of Z-absorbing ${C}^{\ast }$ -algebras . Int. J. Math.. 15(2004), no. 10, 1065–1084.CrossRefGoogle Scholar
Rørdam, M. and Winter, W., The Jiang-Su algebra revisited . J. Reine Angew. Math. 642(2010), 129–155.Google Scholar
Russo, B. and Dye, H., A note on unitary operators in ${C}^{\ast }$ -algebras . Duke Math. J., 33(1966), 413–416.CrossRefGoogle Scholar
Tikuisis, A., White, S., and Winter, W., Quasidiagonality of nuclear ${C}^{\ast }$ -algebras . Ann. Math. 185(2017), 229–284.CrossRefGoogle Scholar
Tikuisis, A. and Winter, W., Decomposition rank of $\mathbf{\mathcal{Z}}$ -stable ${C}^{\ast }$ -algebras . Analysis PDE 7(2014), no. 3, 673–700.CrossRefGoogle Scholar
Toms, A., On the classification problem for nuclear ${C}^{\ast }$ -Algebras . Ann. Math. Second Ser. 167(2008), no. 3, 1029–1044.CrossRefGoogle Scholar
Toms, A. and Winter, W., Strongly self-absorbing ${C}^{\ast }$ -algebras . Trans. Amer. Math. Soc. 359(2007), no. 8, 3999–4029.CrossRefGoogle Scholar
Villadsen, J., Simple ${C}^{\ast }$ -algebras with perforation . J. Funct. Anal. 154(1998), no. 1, 110–116.CrossRefGoogle Scholar
Villadsen, J., On the stable rank of simple ${C}^{\ast }$ -algebras. J. Amer. Math. Soc. 12(1999), no. 4, 1091–1102.CrossRefGoogle Scholar
Voiculescu, D., A note on quasi-diagonal ${C}^{\ast }$ -algebras and homotopy . Duke Math. J. 62(1991), no. 2, 267–271.CrossRefGoogle Scholar
Winter, W., Covering dimension for nuclear ${C}^{\ast }$ -algebras. II . Trans. Amer. Math. Soc. 361(2009), no. 8, 4143–4167.CrossRefGoogle Scholar
Winter, W., Decomposition rank and $\mathbf{\mathcal{Z}}$ -stability . Invent. Math. 179(2010), 229–301.CrossRefGoogle Scholar
Winter, W., Nuclear dimension and $\mathbf{\mathcal{Z}}$ -stability of pure ${C}^{\ast }$ -algebras . Invent. Math. 187(2012), no. 2, 259–342.CrossRefGoogle Scholar
Winter, W., Localizing the Elliott conjecture at strongly self-absorbing ${C}^{\ast }$ -algebras . J. Reine Angew. Math. 692(2014), 193–231.Google Scholar
Winter, W. and Zacharias, J., Completely positive maps of order zero . Münster J. Undergrad. Math. 2(2009), 311–324.Google Scholar
Winter, W. and Zacharias, J., The nuclear dimension of ${C}^{\ast }$ -algebras . Adv. Math. 224(2010), 461–498.CrossRefGoogle Scholar