Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-24T10:28:32.881Z Has data issue: false hasContentIssue false
  • English
  • Français

Schreier families and 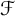$\mathcal {F}$-(almost) greedy bases

Part of: Approximations and expansions Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  14 June 2023

Kevin Beanland Open the ORCID record for Kevin Beanland [Opens in a new window]  and
Hùng Việt Chu Open the ORCID record for Hùng Việt Chu [Opens in a new window]
Kevin Beanland*
Affiliation:
Department of Mathematics, Washington and Lee University, Lexington, VA, USA
Hùng Việt Chu
Affiliation:
Department of Mathematics, University of Illinois Urbana–Champaign, Urbana, IL, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 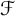$\mathcal {F}$ be a hereditary collection of finite subsets of 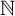$\mathbb {N}$. In this paper, we introduce and characterize 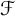$\mathcal {F}$-(almost) greedy bases. Given such a family 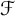$\mathcal {F}$, a basis 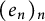$(e_n)_n$ for a Banach space X is called 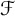$\mathcal {F}$-greedy if there is a constant 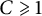$C\geqslant 1$ such that for each 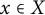$x\in X$, 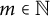$m \in \mathbb {N}$, and 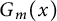$G_m(x)$, we have

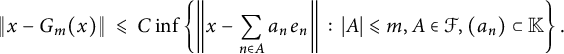$$ \begin{align*} \|x - G_m(x)\|\ \leqslant\ C \inf\left\{\left\|x-\sum_{n\in A}a_ne_n\right\|\,:\, |A|\leqslant m, A\in \mathcal{F}, (a_n)\subset \mathbb{K}\right\}. \end{align*} $$
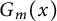Here, $G_m(x)$ is a greedy sum of x of order m, and 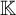$\mathbb {K}$ is the scalar field. From the definition, any 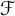$\mathcal {F}$-greedy basis is quasi-greedy, and so the notion of being 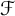$\mathcal {F}$-greedy lies between being greedy and being quasi-greedy. We characterize 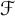$\mathcal {F}$-greedy bases as being 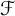$\mathcal {F}$-unconditional, 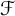$\mathcal {F}$-disjoint democratic, and quasi-greedy, thus generalizing the well-known characterization of greedy bases by Konyagin and Temlyakov. We also prove a similar characterization for 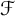$\mathcal {F}$-almost greedy bases.

Furthermore, we provide several examples of bases that are nontrivially 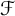$\mathcal {F}$-greedy. For a countable ordinal 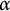$\alpha $, we consider the case 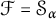$\mathcal {F}=\mathcal {S}_{\alpha }$, where 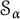$\mathcal {S}_{\alpha }$ is the Schreier family of order 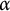$\alpha $. We show that for each 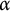$\alpha $, there is a basis that is 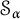$\mathcal {S}_{\alpha }$-greedy but is not 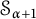$\mathcal {S}_{\alpha +1}$-greedy. In other words, we prove that none of the following implications can be reversed: for two countable ordinals 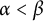$\alpha < \beta $,

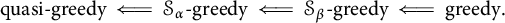$$ \begin{align*} \mbox{quasi-greedy}\ \Longleftarrow\ \mathcal{S}_{\alpha}\mbox{-greedy}\ \Longleftarrow\ \mathcal{S}_{\beta}\mbox{-greedy}\ \Longleftarrow\ \mbox{greedy}. \end{align*} $$

Keywords

Thresholding greedy algorithmSchreier unconditionalSchreier families

MSC classification

Primary: 41A65: Abstract approximation theory (approximation in normed linear spaces and other abstract spaces)
Secondary: 46B15: Summability and bases
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 4 , August 2024 , pp. 1379 - 1399
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The second author acknowledges the summer funding from the Department of Mathematics at the University of Illinois Urbana–Champaign.

References

Albiac, F. and Ansorena, J. L., Characterization of $1$ -almost greedy bases . Rev. Mat. Complut. 30(2017), 13–24.10.1007/s13163-016-0204-3CrossRefGoogle Scholar
Albiac, F. and Kalton, N., Topics in Banach space theory, 2nd ed., Springer, Cham, 2016.10.1007/978-3-319-31557-7CrossRefGoogle Scholar
Albiac, F. and Wojtaszczyk, P., Characterization of $1$ -greedy bases . J. Approx. Theory 138(2006), 65–86.10.1016/j.jat.2005.09.017CrossRefGoogle Scholar
Alspach, D. and Argyros, S. A., Complexity of weakly null sequences . Diss. Math. 321(1992), 1–44.Google Scholar
Argyros, S. A. and Gasparis, I., Unconditional structures of weakly null sequences . Trans. Amer. Math. Soc. 353(2001), 2019–2058.10.1090/S0002-9947-01-02711-8CrossRefGoogle Scholar
Argyros, S. A., Godefroy, G., and Rosenthal, H. P., Descriptive set theory and Banach spaces . In: Johnson, W. B. and Lindenstrauss, J. (eds.), Handbook of the geometry of Banach spaces, Vol. 2, North-Holland, Amsterdam, 2003, pp. 1007–1069.10.1016/S1874-5849(03)80030-XCrossRefGoogle Scholar
Argyros, S. A., Mercourakis, S., and Tsarpalias, A., Convex unconditionality and summability of weakly null sequences . Israel J. Math. 107(1998), 157–193.10.1007/BF02764008CrossRefGoogle Scholar
Argyros, S. A., Motakis, P., and Sari, B., A study of conditional spreading sequences . J. Funct. Anal. 273(2017), 1205–1257.10.1016/j.jfa.2017.04.009CrossRefGoogle Scholar
Argyros, S. A. and Tolias, A., Methods in the theory of hereditarily indecomposable Banach spaces . Mem. Amer. Math. Soc. 170(2004), no. 806, vi + 114.Google Scholar
Beanland, K., Chu, H. V., and Finch-Smith, C. E., Generalized Schreier sets, linear recurrence relation, and Turán graphs . Fibonacci Quart. 60(2022), 352–356.Google Scholar
Bellenot, S. F., Haydon, R., and Odell, E., Quasi-reflexive and tree spaces constructed in the spirit of R. C. James . Contemp. Math. 85(1989), 19–43.10.1090/conm/085/983379CrossRefGoogle Scholar
Berná, P. M., Blasco, O., and Garrigós, G., Lebesgue inequalities for greedy algorithm in general bases . Rev. Mat. Complut. 30(2017), 369–392.10.1007/s13163-017-0221-xCrossRefGoogle Scholar
Dilworth, S. J., Freeman, D., Odell, E., and Schlumprecht, T., Greedy bases for Besov spaces . Constr. Approx. 34(2011), 281–296.10.1007/s00365-010-9115-6CrossRefGoogle Scholar
Dilworth, S. J., Kalton, N. J., Kutzarova, D., and Temlyakov, V. N., The thresholding greedy algorithm, greedy bases, and duality . Constr. Approx. 19(2003), 575–597.10.1007/s00365-002-0525-yCrossRefGoogle Scholar
Konyagin, S. V. and Temlyakov, V. N., A remark on greedy approximation in Banach spaces . East J. Approx. 5(1999), 365–379.Google Scholar
Odell, E., On Schreier unconditional sequences . Contemp. Math. 144(1993), 197–201.10.1090/conm/144/1209461CrossRefGoogle Scholar
Schechtman, G., No greedy bases for matrix spaces with mixed ${\ell}_p$ and ${\ell}_q$ norms . J. Approx. Theory 184(2014), 100–110.10.1016/j.jat.2014.05.004CrossRefGoogle Scholar
Wojtaszczyk, P., Greedy algorithm for general biorthogonal systems . J. Approx. Theory 107(2000), 293–314.10.1006/jath.2000.3512CrossRefGoogle Scholar