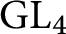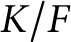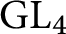Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hultberg, Nuno
and
Mihatsch, Andreas
2025.
A linear AFL for quaternion algebras.
Canadian Journal of Mathematics,
p.
1.