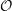Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T05:53:40.306Z Has data issue: false hasContentIssue false
  • English
  • Français

The Primitive Spectrum and Category ${\mathcal{O}}$ for the Periplectic Lie Superalgebra

Part of: Lie algebras and Lie superalgebras Homological methods

Published online by Cambridge University Press:  16 November 2018

Chih-Whi Chen  and
Kevin Coulembier
Chih-Whi Chen
Affiliation:
Department of Mathematics, Uppsala University, Box 480, SE-75106, Uppsala, Sweden
Kevin Coulembier
Affiliation:
School of Mathematics and Statistics, University of Sydney, Australia Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We solve two problems in representation theory for the periplectic Lie superalgebra 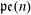$\mathfrak{p}\mathfrak{e}(n)$, namely, the description of the primitive spectrum in terms of functorial realisations of the braid group and the decomposition of category 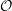${\mathcal{O}}$ into indecomposable blocks.

To solve the first problem, we establish a new type of equivalence between category 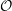${\mathcal{O}}$ for all (not just simple or basic) classical Lie superalgebras and a category of Harish-Chandra bimodules. The latter bimodules have a left action of the Lie superalgebra but a right action of the underlying Lie algebra. To solve the second problem, we establish a BGG reciprocity result for the periplectic Lie superalgebra.

Keywords

Harish-Chandra bimodulesperiplectic Lie superalgebratwisting functorscompletion functorsprimitive spectrumcategory Oblock decomposition

MSC classification

Primary: 16E30: Homological functors on modules (Tor, Ext, etc.)
Secondary: 17B10: Representations, algebraic theory (weights)
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 3 , June 2020 , pp. 625 - 655
Copyright
© Canadian Mathematical Society 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Present address: School of Mathematical Sciences, Xiamen University, Xiamen 361005, China Email: [email protected]

The first author is supported by Vergstiftelsen, and the second author is supported by ARC grant DE170100623.

References

Andersen, H. H. and Stroppel, C., Twisting functors on 𝓞. Represent. Theory 7(2003), 681–699. https://doi.org/10.1090/S1088-4165-03-00189-4.Google Scholar
Arkhipov, S., Semi-infinite cohomology of associative algebras and bar duality. Internat. Math. Res. Notices 1997, no. 17, 833–863. https://doi.org/10.1155/S1073792897000548.Google Scholar
Balagovic, M., Daugherty, Z., Entova-Aizenbud, I., Halacheva, I., Hennig, J., Im, M.-S., Letzter, G., Norton, E., Serganova, V., and Stroppel, C., Translation functors and decomposition numbers for the periplectic Lie superalgebra p(n). Math. Res. Letter 2019, accepted. arxiv:1610.08470.Google Scholar
Bell, A. and Farnsteiner, R., On the theory of Frobenius extensions and its application to Lie superalgebras. Trans. Amer. Math. Soc. 335(1993), no. 1, 407–424. https://doi.org/10.2307/2154275.Google Scholar
Bernstein, J. and Gelfand, S., Tensor products of finite- and infinite-dimensional representations of semisimple Lie algebras. Compositio Math. 41(1980), no. 2, 245–285.Google Scholar
Bernstein, I., Gelfand, I., and Gelfand, S., A certain category of g-modules. Funkcional. Anal. i Prilozen. 10(1976), 1–8.Google Scholar
Chen, C.-W., Finite-dimensional representations of periplectic Lie superalgebras. J. Algebra 443(2015), 99–125. https://doi.org/10.1016/j.jalgebra.2015.06.042.Google Scholar
Chen, C.-W. and Peng, Y.-N., Affine periplectic Brauer algebras. J. Algebra 501(2018), 345–372. https://doi.org/10.1016/j.jalgebra.2018.01.005.Google Scholar
Cheng, S-J., Mazorchuk, V., and Wang, W., Equivalence of blocks for the general linear Lie superalgebra. Lett. Math. Phys. 103(2013), no. 12, 1313–1327. https://doi.org/10.1007/s11005-013-0642-5.Google Scholar
Cheng, S.-J. and Wang, W., Dualities and representations of Lie superalgebras. Graduate Studies in Mathematics, 144, American Mathematical Society, Providence, RI, 2012. https://doi.org/10.1090/gsm/144.Google Scholar
Coulembier, K., The Primitive Spectrum of a basic classical Lie superalgebra. Comm. Math. Phys. 348(2016), no. 2, 579–602. https://doi.org/10.1007/s00220-016-2667-y.Google Scholar
Coulembier, K., The periplectic Brauer algebra. Proc. Lond. Math. Soc. 117(2018), no. 3, 441–482. https://doi.org/10.1112/plms.12137.Google Scholar
Coulembier, K. and Mazorchuk, V., Primitive ideals, twisting functors and star actions for classical Lie superalgebras. J. Reine Angew. Math. 718(2016), 207–253. https://doi.org/10.1515/crelle-2014-0079.Google Scholar
Duflo, M., Sur la classification des idéaux primitifs dans l’algèbre enveloppante d’une algèbre de Lie semi-simple. Ann. of Math. (2) 105(1977), no. 1, 107–120. https://doi.org/10.2307/1971027.Google Scholar
Gorelik, M., The center of a simple p-type Lie superalgebra. J. Algebra 246(2001), 414–428. https://doi.org/10.1006/jabr.2001.8977.Google Scholar
Humphreys, J., Representations of semisimple Lie algebras in the BGG category O. Graduate Studies in Mathematics, 94, American Mathematical Society, Providence, RI, 2008. https://doi.org/10.1090/gsm/094.Google Scholar
Joseph, A., The enright functor on the Bernstein–Gelfand–Gelfand category 𝓞. Invent. Math. 67(1982), no. 3, 423–445. https://doi.org/10.1007/BF01398930.Google Scholar
Kac, V., Representations of classical Lie superalgebras. In: Differential geometrical methods in mathematical physics, II (Proc. Conf., Univ. Bonn, Bonn, 1977), Lecture Notes in Math., 676, Springer, Berlin, 1978, pp. 597–626.Google Scholar
Khomenko, O. and Mazorchuk, V., On Arkhipov’s and Enright’s functors. Math. Z. 249(2005), no. 2, 357–386.Google Scholar
Letzter, E. S., Primitive ideals in finite extensions of Noetherian rings. J. London Math. Soc. 39(1989), no. 3, 427–435. https://doi.org/10.1112/jlms/s2-39.3.427.Google Scholar
Mazorchuk, V. and Miemietz, V., Serre functors for Lie algebras and superalgebras. Ann. Inst. Fourier 62(2012), no. 1, 47–75.Google Scholar
Miličić, D. and Soergel, W., The composition series of modules induced from Whittaker modules. Comment. Math. Helv. 72(1997), no. 4, 503–520. https://doi.org/10.1007/s000140050031.Google Scholar
Musson, I. M., A classification of primitive ideals in the enveloping algebra of a classical simple Lie superalgebra. Adv. Math. 91(1992), 252–268. https://doi.org/10.1016/0001-8708(92)90018-G.Google Scholar
Musson, I. M., Lie superalgebras and enveloping algebras. Graduate Studies in Mathematics, 131, American Mathematical Society, Providence, RI, 2012. https://doi.org/10.1090/gsm/131.Google Scholar
Serganova, V., On representations of the Lie superalgebra p(n). J. Algebra 258(2002), no. 2, 615–630. https://doi.org/10.1016/S0021-8693(02)00645-2.Google Scholar
Vogan, D. A., Ordering of the primitive spectrum of a semisimple Lie algebra. Math. Ann. 248(1980), no. 3, 195–203. https://doi.org/10.1007/BF01420525.Google Scholar