Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T14:45:34.144Z Has data issue: false hasContentIssue false
  • English
  • Français

Potential kernels for radial Dunkl Laplacians

Part of: Lie algebras and Lie superalgebras Markov processes

Published online by Cambridge University Press:  20 April 2021

P. Graczyk ,
T. Luks  and
P. Sawyer
P. Graczyk
Affiliation:
Université d’Angers, CNRS, LAREMA, SFR MATHSTIC, F-49000Angers, France e-mail: [email protected]
T. Luks
Affiliation:
Institut für Mathematik, Universität Paderborn, Warburger Strasse 100, D-33098Paderborn, Germany e-mail: [email protected]
P. Sawyer*
Affiliation:
Department of Mathematics and Computer Science, Laurentian University, Sudbury, ON, Canada
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive two-sided bounds for the Newton and Poisson kernels of the W-invariant Dunkl Laplacian in the geometric complex case when the multiplicity $k(\alpha )=1$ i.e., for flat complex symmetric spaces. For the invariant Dunkl–Poisson kernel $P^{W}(x,y)$ , the estimates are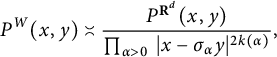

$$ \begin{align*} P^{W}(x,y)\asymp \frac{P^{\mathbf{R}^{d}}(x,y)}{\prod_{\alpha> 0 \ }|x-\sigma_{\alpha} y|^{2k(\alpha)}}, \end{align*} $$
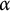where the $\alpha $ ’s are the positive roots of a root system acting in 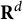$\mathbf {R}^{d}$ , the 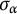$\sigma _{\alpha }$ ’s are the corresponding symmetries and 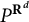$P^{\mathbf {R}^{d}}$ is the classical Poisson kernel in 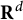${\mathbf {R}^{d}}$ . Analogous bounds are proven for the Newton kernel when 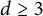$d\ge 3$ .

The same estimates are derived in the rank one direct product case 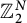$\mathbb {Z}_{2}^{N}$ and conjectured for general W-invariant Dunkl processes.

As an application, we get a two-sided bound for the Poisson and Newton kernels of the classical Dyson Brownian motion and of the Brownian motions in any Weyl chamber.

Keywords

Potential kernelNewton kernelDunkl settingcomplex symmetric spaceroot system

MSC classification

Primary: 17B22: Root systems
Secondary: 60J45: Probabilistic potential theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 4 , August 2022 , pp. 1005 - 1033
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported by Labex CHL Lebesgue and Programme Régional DEFIMATHS. He is grateful to LU and Paderborn for their great hospitality.

The second author is grateful to Université d’Angers and to Laurentian University for their hospitality.

The third author is supported by Laurentian University. The author is thankful to Université d’Angers and to Universität Paderborn for their hospitality.

References

Andraus, S., Katori, M., and Miyashita, S.. Interacting particles on the line and Dunkl intertwining operator of type A: Application to the freezing regime. J. Phys. A Math. Theor. 45(2012), 395201.CrossRefGoogle Scholar
Andraus, S., and Voit, M.. Limit theorems for multivariate Bessel processes in the freezing regime. Stoch. Proc. Appl. 129(2019), no#. 11, 4771–4790. https://doi.org/10.1016/j.spa.2018.12.011 CrossRefGoogle Scholar
Chen, Z.-Q., and Song, R.. Estimates on Green functions and Poisson kernels for symmetric stable processes. Math. Ann. 312(1998), no#. 3, 465–501 CrossRefGoogle Scholar
Cherednik, I.. A unification of the Knizhnik-Zamolodchikov equations and Dunkl operators via affine Hecke algebras. Invent. Math. 106(1991), 411–432 CrossRefGoogle Scholar
Chrouda, M. B.. On the Dirichlet problem associated with the Dunkl Laplacian. Annales Polonici Mathematici. 117(2016), no. 1, 79–87 Google Scholar
Cranston, M., and Zhao, Z.. Conditional transformation of drift formula and potential theory for $\frac{1}{2}\varDelta +b\left(\cdot \right)\cdot \nabla$ . Comm. Math. Phys. 112(1987), 613–625 CrossRefGoogle Scholar
de Jeu, M.. The Dunkl transform. Invent. Math. 113(1993), 147–162 CrossRefGoogle Scholar
Deleaval, L.. Fefferman-Stein inequalities for the  ${\mathbb{Z}}_2^d$ Dunkl maximal operator . J. Math. Anal. Appl. 360(2009), no. 2, 711–726 CrossRefGoogle Scholar
Dunkl, C. F.. Differential-difference operators associated to reflections groups. Trans. Amer. Math. Soc. 311(1989), 167–183 CrossRefGoogle Scholar
Dunkl, C. F.. Integral kernels with reflection group invariance. Canad. J. Math. 43(1991), 1213–1227 CrossRefGoogle Scholar
Dunkl, C. F. and Xu, Y., Orthogonal polynomials of several variables , Encyclopedia of Mathematics and Its Applications, 81. Cambridge University Press, Cambridge, MA, 2001.CrossRefGoogle Scholar
Dyson, F.. A Brownian Motion model for the eigenvalues of a random matrix. J. Math. Phys. 3(1962), 1191–1198 CrossRefGoogle Scholar
Dziubański, J.. Riesz transforms characterizations of Hardy spaces ${H}^1$ for the rational Dunkl setting and multidimensional Bessel operators . J. Geom. Anal. 26(2016), no. 4, 2639–2663 CrossRefGoogle Scholar
Gallardo, L., and Rejeb, C.. A new mean value property for harmonic functions relative to the Dunkl-Laplacian operator and applications. Trans. Amer. Math. Soc. 368(2016), 3727–3753 CrossRefGoogle Scholar
Gallardo, L., and Rejeb, C.. Newtonian potentials and subharmonic functions associated to root systems. Potential Anal. 47(2017), no. 4, 369–400 CrossRefGoogle Scholar
Grabiner, D. J.. Brownian motion in a Weyl chamber, non-colliding particles, and random matrices. Annales de l’I.H.P. Probabilités et statistiques. 35(1999), no. 2, 177–204 Google Scholar
Graczyk, P., Luks, T., and Rösler, M.. On the Green function and Poisson integrals of the Dunkl Laplacian. Potential Anal. 48(2018), no. 3, 337–360 CrossRefGoogle Scholar
Graczyk, P. and Sawyer, P., Integral kernels on complex symmetric spaces and for the Dyson Brownian motion, to appear in the Mathematische Nachrichten, 2021. Preprint, 2019. https://hal.archives-ouvertes.fr/hal-01789322/.Google Scholar
Helgason, S., Groups and geometric analysis. Integral geometry, invariant differential operators, and spherical functions , Mathematical Surveys and Monographs, 83. American Mathematical Society, Providence, RI, 2000.Google Scholar
Helgason, S., Differential geometry, lie groups and symmetric spaces , Graduate Studies in Mathematics, 34. American Mathematical Society, Providence, RI, 2001.Google Scholar
Katori, M., Bessel processes, Schramm–Loewner evolution, and the Dyson model, Springer Briefs in Mathematical Physics, 11, Heidelberg: Springer, 2016.CrossRefGoogle Scholar
Kulczycki, T.. Properties of Green function of symmetric stable processes. Probab. Math. Stat. 17(1997), 339–364 Google Scholar
Lawlor, G. R., A L’Hospital’s rule for multivariable functions, 2012, arXiv:1209.0363, 1–13.Google Scholar
Maslouhi, M., and Yousffi, E. H.. Harmonic functions associated to Dunkl operators. Monatsh. Math. 152(2007), 337–345 CrossRefGoogle Scholar
Maslouhi, M., and Yousffi, E. H.. The Dunkl intertwining operator. J. Funct. Anal. 256(2009), 2697–2709 CrossRefGoogle Scholar
Nowak, A., and Stempak, K.. Riesz transforms for the Dunkl harmonic oscillator. Math. Z. 262(2009), no. 3, 539–556 CrossRefGoogle Scholar
Nowak, A., and Stempak, K.. Negative powers of Laguerre operators. Canad. J. Math. 64(2012), no. 1, 183–216 CrossRefGoogle Scholar
Nowak, A., Stempak, K. and Szarek, T. Z., On harmonic analysis operators in Laguerre-Dunkl and Laguerre-symmetrized settings. SIGMA Symmetry Integr. Geom. Methods Appl. 12(2016), no. 096, 39 pp.Google Scholar
Revuz, D., and Yor, M.. 3rd ed., Continuous Martingales and Brownian motion , 3rd ed., Springer, New York, NY, 2005.Google Scholar
Rösler, M.. Generalized Hermite polynomials and the heat equation for Dunkl operators. Commun. Math. Phys. 192(1998), 519–541 Google Scholar
Rösler, M.. Positivity of Dunkl’s intertwining operator. Duke Math. J. 98(1999), 445–463 CrossRefGoogle Scholar
Rösler, M. and Voit, M., Dunkl theory, convolutions algebras, and related Markov processes . In: Graczyk, P., Rösler, M., and Yor, M. (eds.), Harmonic and stochastic analysis of Dunkl processes, Travaux en cours 71, Hermann Mathématiques, 2008.Google Scholar
Sawyer, P.. A Laplace-type representation of the generalized spherical functions associated with the root systems of type  $A$ . Mediterr. J. Math. 14(2017), 147. https://doi.org/10.1007/s00009-017-0948-0 CrossRefGoogle Scholar
Thangavelu, S., and Xu, Y.. Convolution operator and maximal function for the Dunkl transform. J. Anal. Math. 97(2005), 25–55 CrossRefGoogle Scholar
Widman, K.-O.. Inequalities for the Green function and boundary continuity of the gradient of solutions of elliptic differential equations. Math. Scand. 21(1967), 17–37 CrossRefGoogle Scholar
Xu, Y.. Orthogonal polynomials for a family of product weight functions on the spheres. Can. J. Math. 49(1997), no. 1, 175–192 CrossRefGoogle Scholar
Zhao, Z.. Uniform boundedness of conditional gauge and Schrödinger equations. Comm. Math. Phys. 93(1984), 19–31 CrossRefGoogle Scholar
Zhao, Z.. Green function for Schrödinger operator and conditioned Feynman-Kac gauge. J. Math. Anal. Appl. 116(1986), 309–334 CrossRefGoogle Scholar