Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T16:06:10.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Orlicz Addition for Measures and an Optimization Problem for the 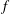$f$-divergence

Part of: Foundations of probability theory Functions of several variables Communication, information Classical measure theory General convexity

Published online by Cambridge University Press:  16 July 2019

Shaoxiong Hou  and
Deping Ye
Shaoxiong Hou
Affiliation:
College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang, Hebei Province, 050024, P. R. China Department of Mathematics and Statistics, Memorial University, St. John’s, NL A1C 5S7 Email: [email protected]@mun.ca
Deping Ye
Affiliation:
College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang, Hebei Province, 050024, P. R. China Department of Mathematics and Statistics, Memorial University, St. John’s, NL A1C 5S7 Email: [email protected]@mun.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper provides a functional analogue of the recently initiated dual Orlicz–Brunn–Minkowski theory for star bodies. We first propose the Orlicz addition of measures, and establish the dual functional Orlicz–Brunn–Minkowski inequality. Based on a family of linear Orlicz additions of two measures, we provide an interpretation for the famous 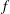$f$-divergence. Jensen’s inequality for integrals is also proved to be equivalent to the newly established dual functional Orlicz–Brunn–Minkowski inequality. An optimization problem for the 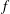$f$-divergence is proposed, and related functional affine isoperimetric inequalities are established.

Keywords

affine isoperimetric inequalitydual Brunn–Minkowski theoryf-divergenceoptimization problem for the f-divergence

MSC classification

Primary: 52A41: Convex functions and convex programs
Secondary: 26B25: Convexity, generalizations 28A25: Integration with respect to measures and other set functions 60A10: Probabilistic measure theory 94A15: Information theory, general 94A17: Measures of information, entropy
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 2 , April 2020 , pp. 455 - 479
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of S. H. has been partially supported by CSC (No. 201306040135) and by the Science Foundation of Hebei Normal University (No. L2018B32). The research of D. Y. is supported by a NSERC grant.

References

Ali, M. and Silvey, D., A general class of coefficients of divergence of one distribution from another. J. R. Statist. Soc. Ser. B 28(1966), 131–142.Google Scholar
Artstein-Avidan, S., Klartag, B., and Milman, V., The Santaló point of a function, and a functional form of the Santaló inequality. Mathematika 51(2004), 33–48. https://doi.org/10.1112/S0025579300015497Google Scholar
Artstein-Avidan, S., Klartag, B., Schütt, C., and Werner, E., Functional affine-isoperimetry and an inverse logarithmic Sobolev inequality. J. Funct. Anal. 262(2012), 4181–4204. https://doi.org/10.1016/j.jfa.2012.02.014Google Scholar
Barron, A., Györfi, L., and van der Meulen, E., Distribution estimates consistent in total variation and two types of information divergence. IEEE Trans. Inform. Theory 38(1990), 1437–1454.Google Scholar
Bhattacharyya, A., On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 35(1943), 99–109.Google Scholar
Blaschke, W., Vorlesungen über Differentialgeometrie II. In: Affine Differentialgeometrie. Springer-Verlag, Berlin, 1923.Google Scholar
Caglar, U., Fradelizi, M., Guedon, O., Lehec, J., Schuett, C., and Werner, E., Functional versions of L p-affine surface area and entropy inequalities. Int. Math. Res. Not. IMRN 2016(2016), 1223–1250.Google Scholar
Caglar, U. and Werner, E., Divergence for s-concave and log concave functions. Adv. Math. 257(2014), 219–247. https://doi.org/10.1016/j.aim.2014.02.013Google Scholar
Caglar, U. and Ye, D., Affine isoperimetric inequalities in the functional Orlicz–Brunn–Minkowski theory. Adv. Appl. Math. 81(2016), 78–114. https://doi.org/10.1016/j.aam.2016.06.007Google Scholar
Cover, T. and Thomas, J., Elements of information theory. Second ed., Wiley-Interscience, Hoboken, NJ, 2006.Google Scholar
Csiszár, I., Eine informationstheoretische Ungleichung und ihre Anwendung auf den Beweis der Ergodizität von Markoffschen Ketten. Publ. Math. Inst. Hungar. Acad. Sci. Ser. A 8(1963), 84–108.Google Scholar
Csiszár, I., I-divergence geometry of probability distributions and minimization problems. Ann. Probab. 3(1975), 146–158. https://doi.org/10.1214/aop/1176996454Google Scholar
Fradelizi, M. and Meyer, M., Some functional forms of Blaschke–Santaló inequality. Math. Z. 256(2007), 379–395. https://doi.org/10.1007/s00209-006-0078-zGoogle Scholar
Frank, N. and Nock, R., On the Chi square and higher-order Chi distances for approximating f-Divergences. IEEE Signal Process. Lett. 21(2014), 10–13.Google Scholar
Gardner, R., A positive answer to the Busemann–Petty problem in three dimensions. Ann. of Math. 140(1994), 435–447. https://doi.org/10.2307/2118606Google Scholar
Gardner, R., The Brunn–Minkowski inequality. Bull. Amer. Math. Soc. 39(2002), 355–405. https://doi.org/10.1090/S0273-0979-02-00941-2Google Scholar
Gardner, R., Hug, D., and Weil, W., The Orlicz–Brunn–Minkowski theory: A general framework, additions, and inequalities. J. Differential Geom. 97(2014), 427–476.Google Scholar
Gardner, R., Hug, D., Weil, W., and Ye, D., The dual Orlicz–Brunn–Minkowski theory. J. Math. Anal. Appl. 430(2015), 810–829. https://doi.org/10.1016/j.jmaa.2015.05.016Google Scholar
Gardner, R. and Kiderlen, M., Operations between functions. Comm. Anal. Geom. 26(2018), 787–855. https://doi.org/10.4310/CAG.2018.v26.n4.a5Google Scholar
Gardner, R., Koldobski, A., and Schlumprecht, T., An analytic solution to the Busemann–Petty problem on sections of convex bodies. Ann. of Math. 149(1999), 691–703. https://doi.org/10.2307/120978Google Scholar
Good, I., Maximum entropy for hypothesis formulation, especially for multidimensional contingency tables. Ann. Math. Statist. 34(1963), 911–934. https://doi.org/10.1214/aoms/1177704014Google Scholar
Haberl, C. and Parapatits, L., The centro-affine Hadwiger theorem. J. Amer. Math. Soc. 27(2014), 685–705. https://doi.org/10.1090/S0894-0347-2014-00781-5Google Scholar
Harremoes, P. and Topsoe, F., Inequalities between entropy and the index of coincidence derived from information diagrams. IEEE Trans. Inform. Theory 47(2001), 2944–2960. https://doi.org/10.1109/18.959272Google Scholar
Ireland, C. and Kullback, S., Contingency tables with given marginals. Biometrika 55(1968), 179–188. https://doi.org/10.1093/biomet/55.1.179Google Scholar
Jaynes, E., Information theory and statistical mechanics. Phys. Rev. 106(1957), 620–630.Google Scholar
Kullback, S. and Leibler, R., On information and sufficiency. Ann. Math. Statist. 22(1951), 79–86. https://doi.org/10.1214/aoms/1177729694Google Scholar
Lehec, J., Partitions and functional Santaló inequalities. Arch. Math. (Basel) 92(2009), 89–94.Google Scholar
Liese, F. and Vajda, I., On divergences and information in statistics and information theory. IEEE Trans. Inform. Theory 52(2006), 4394–4412. https://doi.org/10.1109/TIT.2006.881731Google Scholar
Ludwig, M., General affine surface areas. Adv. Math. 224(2010), 2346–2360. https://doi.org/10.1016/j.aim.2010.02.004Google Scholar
Ludwig, M. and Reitzner, M., A characterization of affine surface area. Adv. Math. 147(1999), 138–172. https://doi.org/10.1006/aima.1999.1832Google Scholar
Ludwig, M. and Reitzner, M., A classification of SL (n) invariant valuations. Ann. of Math. 172(2010), 1219–1267. https://doi.org/10.4007/annals.2010.172.1223Google Scholar
Lutwak, E., Intersection bodies and dual mixed volume. Adv. Math. 71(1988), 232–261. https://doi.org/10.1016/0001-8708(88)90077-1Google Scholar
Lutwak, E., The Brunn–Minkowski–Firey theory. II. Affine and geominimal surface areas. Adv. Math. 118(1996), 244–294. https://doi.org/10.1006/aima.1996.0022Google Scholar
Morimoto, T., Markov processes and the H-theorem. J. Phys. Soc. Japan 18(1963), 328–331. https://doi.org/10.1143/JPSJ.18.328Google Scholar
Österreicher, F. and Vajda, I., A new class of metric divergences on probability spaces and its applicability in statistics. Ann. Inst. Statist. Math. 55(2003), 639–653. https://doi.org/10.1007/BF02517812Google Scholar
Petty, C. M., Geominimal surface area. Geom. Dedicata 3(1974), 77–97. https://doi.org/10.1007/BF00181363Google Scholar
Rényi, A., On measures of entropy and information. Proc. 4th Berkeley Sympos. Math. Statist. and Prob., 1, Univ. California Press, Berkeley, CA, 1961, pp. 547–561.Google Scholar
Sanov, I., On the probability of large deviations of random magnitudes. (Russian), Mat. Sbornik 42(1957), 11–44.Google Scholar
Schütt, C. and Werner, E., Surface bodies and p-affine surface area. Adv. Math. 187(2004), 98–145. https://doi.org/10.1016/j.aim.2003.07.018Google Scholar
Werner, E., Rényi divergence and L p-affine surface area for convex bodies. Adv. Math. 230(2012), 1040–1059. https://doi.org/10.1016/j.aim.2012.03.015Google Scholar
Xi, D., Jin, H., and Leng, G., The Orlicz Brunn–Minkowski inequality. Adv. Math. 260(2014), 350–374. https://doi.org/10.1016/j.aim.2014.02.036Google Scholar
Ye, D., New Orlicz affine isoperimetric inequalities. J. Math. Anal. Appl. 427(2015), 905–929. https://doi.org/10.1016/j.jmaa.2015.02.084Google Scholar
Ye, D., L p Geominimal surface areas and their inequalities. Int. Math. Res. Not. IMRN 2015(2015), 2465–2498. https://doi.org/10.1093/imrn/rnu009Google Scholar
Ye, D., Dual Orlicz–Brunn–Minkowski theory: dual Orlicz L 𝜙 affine and geominimal surface areas. J. Math. Anal. Appl. 443(2016), 352–371. https://doi.org/10.1016/j.jmaa.2016.05.027Google Scholar
Zhang, G., A positive answer to the Busemann–Petty problem in four dimensions. Ann. of Math. 149(1999), 535–543. https://doi.org/10.2307/120974Google Scholar
Zhu, B., Xing, S., and Ye, D., The dual Orlicz–Minkowski problem. J. Geom. Anal. 28(2018), 3829–3855. https://doi.org/10.1007/s12220-018-0002-xGoogle Scholar
Zhu, B., Zhou, J., and Xu, W., Dual Orlicz–Brunn–Minkowski theory. Adv. Math. 264(2014), 700–725. https://doi.org/10.1016/j.aim.2014.07.019Google Scholar