Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-26T16:52:41.298Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Skolem problem and some related questions for parametric families of linear recurrence sequences

Part of: Sequences and sets Diophantine equations

Published online by Cambridge University Press:  08 February 2021

Alina Ostafe  and
Igor E. Shparlinski
Alina Ostafe*
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, Australia, NSW2052 e-mail: [email protected]
Igor E. Shparlinski
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, Australia, NSW2052 e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that in a parametric family of linear recurrence sequences 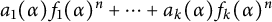$a_1(\alpha ) f_1(\alpha )^n + \cdots + a_k(\alpha ) f_k(\alpha )^n$ with the coefficients 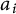$a_i$ and characteristic roots 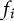$f_i$ , 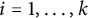$i=1, \ldots ,k$ , given by rational functions over some number field, for all but a set of elements 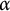$\alpha $ of bounded height in the algebraic closure of 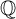${\mathbb Q}$ , the Skolem problem is solvable, and the existence of a zero in such a sequence can be effectively decided. We also discuss several related questions.

Keywords

Skolem problemperfect powerlinear recurrence sequence

MSC classification

Primary: 11B37: Recurrences 11D61: Exponential equations
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 3 , June 2022 , pp. 773 - 792
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ailon, N. and Rudnick, Z., Torsion points on curves and common divisors of ${a}^k-1$ and ${b}^k-1$ . Acta Arith. 113(2004), 31–38.CrossRefGoogle Scholar
Amoroso, F., Masser, D., and Zannier, U., Bounded height in pencils of finitely generated subgroups, Dule Math. J. 166(2017), 2599–2642.Google Scholar
Amoroso, F. and Viada, E., On the zeros of linear recurrence sequences. Acta Arith. 147(2011), 387–396.CrossRefGoogle Scholar
Bell, J. P., Nguyen, K. D., and Zannier, U., $D$ -finiteness, rationality, and height. Trans. Amer. Math. Soc. 373(2020), 4889–4906.CrossRefGoogle Scholar
Berstel, J. and Mignotte, M., Deux propriétés décidables des suites récurrentes linéaires. Bull. Soc. Math. France 104(1976), 175–184.CrossRefGoogle Scholar
Beukers, F. and Smyth, C. J., Cyclotomic points on curves . In: Number Theory for the Millenium (Urbana, Illinois, 2000). Vol. I, A. K. Peters, Natick, MA, 2002, pp. 67–85.Google Scholar
Bilu, Y. and Luca, F., Binary polynomial power sums vanishing at roots of unity. Acta Arith., to appear.Google Scholar
Bombieri, E. and Gubler, W., Heights in diophantine geometry . Cambridge University Press, Cambridge, UK, 2006.Google Scholar
Bombieri, E., Habegger, P., Masser, D., and Zannier, U., A note on Maurin theorem. Rend. Lincei Mat. Appl. 21(2010), 251–260.Google Scholar
Bombieri, E., Masser, D., and Zannier, U., Intersecting a curve with algebraic subgroups of multiplicative groups. Int. Math. Res. Not. 20(1999), 1119–1140.CrossRefGoogle Scholar
Bombieri, E., Masser, D., and Zannier, U., On unlikely intersections of complex varieties with tori. Acta Arith. 133(2008), 309–323.CrossRefGoogle Scholar
Brindza, B., Zeros of polynomials and exponential diophantine equations. Compos. Math. 61(1987), 137–157.Google Scholar
Brownawell, W. D. and Masser, D., Vanishing sums in function fields. Math. Proc. Cambridge Philos. Soc. 100(1986), 427–434.CrossRefGoogle Scholar
Bugeaud, Y., Corvaja, P., and Zannier, U., An upper bound for the G.C.D. of ${a}^n-1$ and ${b}^n-1$ . Math. Z. 243(2003), 79–84.CrossRefGoogle Scholar
Corvaja, P. and Zannier, U., A lower bound for the height of a rational function at $S$ -unit points. Monatsh. Math. 144(2005), 203–224.CrossRefGoogle Scholar
Corvaja, P. and Zannier, U., Some cases of Vojta’s conjecture on integral points over function fields. J. Algebraic Geom. 17(2008), 295–333.CrossRefGoogle Scholar
Dubickas, A. and Sha, M., The distance to square-free polynomials. Acta Arith. 186(2018), 243–256.CrossRefGoogle Scholar
Everest, G., van der Poorten, A. J., Shparlinski, I. E., and Ward, T. B., Recurrence sequences. American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Fuchs, C., Polynomial-exponential equations and linear recurrences. Glas. Mat. 38(2003), 233–252.CrossRefGoogle Scholar
Fuchs, C. and Heintze, S., On the growth of linear recurrences in function fields. Acta Arith., to appear.Google Scholar
Fuchs, C. and Pethö, A., Effective bounds for the zeros of linear recurrences in function fields. J. Théor. Nombr. Bordx. 17(2005), 749–766.CrossRefGoogle Scholar
Hindry, M. and Silverman, J. H., Diophantine geometry. Graduate Texts in Mathematics, 201, Springer, New York, NY, 2000.CrossRefGoogle Scholar
Koblitz, N., P-adic numbers, p-adic analysis, and zeta-functions. Springer-Verlag, New York, NY, 1977.CrossRefGoogle Scholar
Kulkarni, A., Mavraki, N. M., and Nguyen, K. D., Algebraic approximations to linear combinations of powers: an extension of results by Mahler and Corvaja–Zannier. Trans. Amer. Math. Soc. 371(2019), 3787–3804.CrossRefGoogle Scholar
Lang, S., Division points on curves. Ann. Mat. Pura Appl. 70(1965), 229–234.CrossRefGoogle Scholar
Levin, A., Greatest common divisors and Vojta's conjecture for blowups of algebraic tori. Invent. Math. 215(2019), no. 2, 493–533.CrossRefGoogle Scholar
Levin, A. and Wang, J. T.-Y., Greatest common divisors of analytic functions and Nevanlinna theory of algebraic tori. J. Reine Angew. Math. 767(2020), 77–107.CrossRefGoogle Scholar
Lidl, R. and Niederreiter, H., Finite fields. Cambridge University Press, Cambridge, UK, 1997.Google Scholar
Mason, R. C., Diophantine equations over function fields. London Mathematical Society Lecture Note Series, 96, Cambridge University Press, Cambridge, UK, 1984.CrossRefGoogle Scholar
Maurin, G., Courbes algébriques et équations multiplicatives. Math. Ann. 341(2008), 789–824.CrossRefGoogle Scholar
Ostafe, A., On some extensions of the Ailon–Rudnick theorem. Monatsh Math. 181(2016), 451–471.CrossRefGoogle Scholar
Pakovich, F. and Shparlinski, I. E., Level curves of rational functions and unimodular points on rational curves. Proc. Amer. Math. Soc. 148(2020), 1829–1833.CrossRefGoogle Scholar
Sha, M., Effective results on the Skolem problem for linear recurrence sequences. J. Number Theory 197(2019), 228–249.CrossRefGoogle Scholar
Shparlinski, I. E., Prime divisors of recurrent sequences. Izv. Vyssh. Uchebn. Zaved. Mat. 215(1980), no. 4, 101–103.Google Scholar
Silverman, J. H., The S-unit equation over function fields. Proc. Cambridge. Philos. Soc. 95(1984), 3–4.CrossRefGoogle Scholar
Silverman, J. H., The arithmetic of dynamical systems. Springer-Verlag, New York, NY, 2007.CrossRefGoogle Scholar
Stewart, C. L., On divisors of terms of linear recurrence sequences. J. Reine Angew. Math. 333(1982), 12–31.Google Scholar
Stewart, C. L., On the greatest square-free factor of terms of a linear recurrence sequence. In: Diophantine equations, Tata Institute of Fundamental Research Studies in Mathematics, 20, Tata Institute of Fundamental Research, Mumbai, 2008, pp. 257–264.Google Scholar
Stothers, W. W., Polynomial identities and Hauptmoduln. Q. J. Math. (Oxford) 32(1981), 349–370.CrossRefGoogle Scholar
Voloch, J. F., Diagonal equations over function fields. Bull. Braz. Math. Soc. 16(1985), 29–39.CrossRefGoogle Scholar
Zannier, U., Lecture notes on diophantine analysis. Publications of the Scuola Normale Superiore, Pisa, 2009.Google Scholar