Hostname: page-component-6587cd75c8-4pd2k Total loading time: 0 Render date: 2025-04-24T08:52:03.466Z Has data issue: false hasContentIssue false
  • English
  • Français

A Measurable Selector in Kadison’s Carpenter’s Theorem

Part of: Special classes of linear operators Normed linear spaces and Banach spaces; Banach lattices Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  16 July 2019

Marcin Bownik  and
Marcin Szyszkowski
Marcin Bownik
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403–1222, USA Email: [email protected]
Marcin Szyszkowski
Affiliation:
Faculty of Applied Physics and Mathematics, Department of Probability and Biomathematics,Gdańsk Univerity of Technology, ul. Narutowicza 11/12, 80-233Gdańsk, Poland Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show the existence of a measurable selector in Carpenter’s Theorem due to Kadison. This solves a problem posed by Jasper and the first author in an earlier work. As an application we obtain a characterization of all possible spectral functions of shift-invariant subspaces of 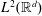$L^{2}(\mathbb{R}^{d})$ and Carpenter’s Theorem for type 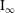$\text{I}_{\infty }$ von Neumann algebras.

Keywords

Schur–Horn problemdiagonal of self-adjoint operatorCarpenter’s theorem

MSC classification

Primary: 42C15: General harmonic expansions, frames
Secondary: 47B15: Hermitian and normal operators (spectral measures, functional calculus, etc.) 46C05: Hilbert and pre-Hilbert spaces
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 6 , December 2020 , pp. 1505 - 1528
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Author M. B. was supported in part by the NSF grant DMS-1665056.

References

Argerami, M., Majorisation and the Carpenter’s theorem. Integral Equations Operator Theory 82(2015), 33–49. https://doi.org/10.1007/s00020-014-2180-7CrossRefGoogle Scholar
Argerami, M. and Massey, P., A Schur–Horn theorem in II 1 factors. Indiana Univ. Math. J. 56(2007), 2051–2059. https://doi.org/10.1512/iumj.2007.56.3113CrossRefGoogle Scholar
Argerami, M. and Massey, P., Towards the Carpenter’s theorem. Proc. Amer. Math. Soc. 137(2009), 3679–3687. https://doi.org/10.1090/S0002-9939-09-09999-7CrossRefGoogle Scholar
Argerami, M. and Massey, P., Schur–Horn theorems in II ∞ factors. Pacific J. Math. 261(2013), 283–310. https://doi.org/10.2140/pjm.2013.261.283CrossRefGoogle Scholar
Antezana, J., Massey, P., Ruiz, M., and Stojanoff, D., The Schur–Horn theorem for operators and frames with prescribed norms and frame operator. Illinois J. Math. 51(2007), 537–560.CrossRefGoogle Scholar
Arveson, W., Diagonals of normal operators with finite spectrum. Proc. Natl Acad. Sci. USA 104(2007), 1152–1158. https://doi.org/10.1073/pnas.0605367104CrossRefGoogle ScholarPubMed
Arveson, W. and Kadison, R., Diagonals of self-adjoint operators. In: Operator theory, operator algebras, and applications. Contemp. Math., 414, Amer. Math. Soc., Providence, RI, 2006, pp. 247–263.https://doi.org/10.1090/conm/414/07814CrossRefGoogle Scholar
Benac, M. J., Massey, P., and Stojanoff, D., Frames of translates with prescribed fine structure in shift invariant spaces. J. Funct. Anal. 271(2016), 2631–2671. https://doi.org/10.1016/j.jfa.2016.07.007CrossRefGoogle Scholar
Benac, M. J., Massey, P., and Stojanoff, D., Convex potentials and optimal shift generated oblique duals in shift invariant spaces. J. Fourier Anal. Appl. 23(2017), 401–441. https://doi.org/10.1007/s00041-016-9474-xCrossRefGoogle Scholar
Bhat, B. and Ravichandran, M., The Schur–Horn theorem for operators with finite spectrum. Proc. Am. Math. Soc. 142(2014), 3441–3453. https://doi.org/10.1090/S0002-9939-2014-12114-9CrossRefGoogle Scholar
Blackadar, B., Operator algebras. Theory of C*-algebras and von Neumann algebras. Encyclopaedia of Mathematical Sciences, 122, Operator Algebras and Non-commutative Geometry, III, Springer-Verlag, Berlin, 2006. https://doi.org/10.1007/3-540-28517-2Google Scholar
Boor, C. de, DeVore, R. A., and Ron, A., The structure of finitely generated shift-invariant spaces in L 2(ℝd). J. Funct. Anal. 119(1994), 37–78. https://doi.org/10.1006/jfan.1994.1003Google Scholar
Boor, C. de, DeVore, R. A., and Ron, A., Approximation orders of FSI spaces in L 2(ℝd). Constr. Approx. 14(1998), 631–652. https://doi.org/10.1007/s003659900094CrossRefGoogle Scholar
Bownik, M., The structure of shift-invariant subspaces of L 2(ℝn). J. Funct. Anal. 177(2000), 282–309. https://doi.org/10.1006/jfan.2000.3635CrossRefGoogle Scholar
Bownik, M. and Jasper, J., Characterization of sequences of frame norms. J. Reine Angew. Math. 654(2011), 219–244. https://doi.org/10.1515/CRELLE.2011.035Google Scholar
Bownik, M. and Jasper, J., Constructive proof of the Carpenter’s theorem. Canad. Math. Bull. 57(2014), 463–476. https://doi.org/10.4153/CMB-2013-037-xCrossRefGoogle Scholar
Bownik, M. and Jasper, J., The Schur–Horn theorem for operators with finite spectrum. Trans. Amer. Math. Soc. 367(2015), 5099–5140. https://doi.org/10.1090/S0002-9947-2015-06317-XCrossRefGoogle Scholar
Bownik, M. and Ross, K., The structure of translation-invariant spaces on locally compact abelian groups. J. Fourier Anal. Appl. 21(2015), 849–884. https://doi.org/10.1007/s00041-015-9390-5CrossRefGoogle Scholar
Bownik, M. and Rzeszotnik, Z., The spectral function of shift-invariant spaces. Michigan Math. J. 51(2003), 387–414. https://doi.org/10.1307/mmj/1060013204Google Scholar
Bownik, M. and Rzeszotnik, Z., The spectral function of shift-invariant spaces on general lattices. In: Wavelets, frames and operator theory. Contemp. Math., 345, Amer. Math. Soc., Providence, RI, 2004, pp. 49–59.https://doi.org/10.1090/conm/345/06240CrossRefGoogle Scholar
Casazza, P., Fickus, M., Mixon, D., Wang, Y., and Zhou, Z., Constructing tight fusion frames. Appl. Comput. Harmon. Anal. 30(2011), 175–187. https://doi.org/10.1016/j.acha.2010.05.002CrossRefGoogle Scholar
Dixmier, J., von Neumann algebras. North-Holland Mathematical Library, 27, North-Holland Publishing Co., Amsterdam-New York, 1981.Google Scholar
Dutkay, D., The local trace function of shift invariant subspaces. J. Operator Theory 52(2004), 267–291.Google Scholar
Dykema, K., Fang, J., Hadwin, D., and Smith, R., The carpenter and Schur–Horn problems for masas in finite factors. Illinois J. Math. 56(2012), 1313–1329.CrossRefGoogle Scholar
Gu, Q. and Han, D., Frames, modular functions for shift-invariant subspaces and FMRA wavelet frames. Proc. Amer. Math. Soc. 133(2005), 815–825. https://doi.org/10.1090/S0002-9939-04-07601-4CrossRefGoogle Scholar
Helson, H., Lectures on invariant subspaces. Academic Press, New York-London, 1964.Google Scholar
Helson, H., The spectral theorem. Lecture Notes in Mathematics, 1227, Springer-Verlag, Berlin, 1986. https://doi.org/10.1007/BFb0101629CrossRefGoogle Scholar
Horn, A., Doubly stochastic matrices and the diagonal of a rotation matrix. Amer. J. Math. 76(1954), 620–630. https://doi.org/10.2307/2372705CrossRefGoogle Scholar
Jasper, J., The Schur–Horn theorem for operators with three point spectrum. J. Funct. Anal. 265(2013), 1494–1521. https://doi.org/10.1016/j.jfa.2013.06.024CrossRefGoogle Scholar
Kadison, R., The Pythagorean theorem. I. The finite case. Proc. Natl. Acad. Sci. USA 99(2002), 4178–4184. https://doi.org/10.1073/pnas.032677199CrossRefGoogle ScholarPubMed
Kadison, R., The Pythagorean theorem. II. The infinite discrete case. Proc. Natl. Acad. Sci. USA 99(2002), 5217–5222. https://doi.org/10.1073/pnas.032677299CrossRefGoogle ScholarPubMed
Kaftal, V. and Loreaux, J., Kadison’s Pythagorean theorem and essential codimension. Integral Equations Operator Theory 87(2017), 565–580. https://doi.org/10.1007/s00020-017-2365-yCrossRefGoogle Scholar
Kaftal, V. and Weiss, G., An infinite dimensional Schur–Horn theorem and majorization theory. J. Funct. Anal. 259(2010), 3115–3162. https://doi.org/10.1016/j.jfa.2010.08.018CrossRefGoogle Scholar
Kennedy, M. and Skoufranis, P., The Schur–Horn problem for normal operators. Proc. Lond. Math. Soc. 111(2015), 354–380. https://doi.org/10.1112/plms/pdv030CrossRefGoogle Scholar
Kennedy, M. and Skoufranis, P., Majorization and a Schur–Horn Theorem for positive compact operators, the nonzero kernel case. J. Funct. Anal. 268(2015), 703–731. https://doi.org/10.1016/j.jfa.2014.10.020Google Scholar
Marshall, A. W., Olkin, I., and Arnold, B. C., Inequalities: theory of majorization and its applications, Second ed., Springer Series in Statistics, Springer, New York, 2011. https://doi.org/10.1007/978-0-387-68276-1CrossRefGoogle Scholar
Massey, P. and Ravichandran, M., Multivariable Schur–Horn theorems. Proc. Lond. Math. Soc. 112(2016), 206–234. https://doi.org/10.1112/plms/pdv067CrossRefGoogle Scholar
Ravichandran, M., The Schur–Horn theorem in von Neumann algebras. arxiv:1209.0909Google Scholar
Ron, A. and Shen, Z., Affine systems in L 2(ℝd): the analysis of the analysis operator. J. Funct. Anal. 148(1997), 408–447. https://doi.org/10.1006/jfan.1996.3079CrossRefGoogle Scholar
Ron, A. and Shen, Z., Weyl-Heisenberg frames and Riesz bases in L 2(ℝd). Duke Math. J. 89(1997), 237–282. https://doi.org/10.1215/S0012-7094-97-08913-4CrossRefGoogle Scholar
Schur, I., Über eine Klasse von Mittelbildungen mit Anwendungen auf die Determinantentheorie. Sitzungsber. Berl. Math. Ges. 22(1923), 9–20.Google Scholar