Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T17:54:06.510Z Has data issue: false hasContentIssue false
  • English
  • Français

LYZ Matrices and SL($n$) Contravariant Valuations on Polytopes

Part of: Polytopes and polyhedra General convexity

Published online by Cambridge University Press:  18 December 2019

Dan Ma  and
Wei Wang
Dan Ma
Affiliation:
Department of Mathematics, Shanghai Normal University, Shanghai, 200234, P.R.China, Email: [email protected]
Wei Wang
Affiliation:
School of Mathematics and Computational Science, Hunan University of Science and Technology, Xiangtan, 411201, P.R. China, Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

All SL($n$) contravariant symmetric matrix valued valuations on convex polytopes in 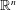$\mathbb{R}^{n}$ are completely classified without any continuity assumptions. The general Lutwak–Yang–Zhang matrix is shown to be essentially the unique such valuation.

Keywords

LYZ matrixvaluationconvex polytopeSL(n) contravariance

MSC classification

Primary: 52B45: Dissections and valuations (Hilbert's third problem, etc.)
Secondary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces)
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 2 , April 2021 , pp. 383 - 398
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work of the first author was supported in part by Shanghai Sailing Program (17YF1413800) and the National Natural Science Foundation of China (11701373). The work of the second author was supported in part by the Natural Science Foundation of Hunan Province (2017JJ3085 and 2019JJ50172).

References

Alesker, S., Continuous rotation invariant valuations on convex sets. Ann. of Math. (2) 149(1999), 977–1005. https://doi.org/10.2307/121078CrossRefGoogle Scholar
Alesker, S., Description of translation invariant valuations on convex sets with solution of P. McMullen’s conjecture. Geom. Funct. Anal. 11(2001), 244–272. https://doi.org/10.1007/PL00001675CrossRefGoogle Scholar
Alesker, S., Bernig, A., and Schuster, F. E., Harmonic analysis of translation invariant valuations. Geom. Funct. Anal. 21(2011), 751–773. https://doi.org/10.1007/s00039-011-0125-8CrossRefGoogle Scholar
Ball, K., Volume ratios and a reverse isoperimetric inequality. J. London Math. Soc. (2) 44(1991), 351–359. https://doi.org/10.1112/jlms/s2-44.2.351CrossRefGoogle Scholar
Ball, K., Ellipsoids of maximal volume in convex bodies. Geom. Dedicata 41(1992), 241–250. https://doi.org/10.1007/BF00182424CrossRefGoogle Scholar
Bernig, A. and Hug, D., Kinematic formulas for tensor valuations. J. Reine Angew. Math. 736(2018), 141–191. https://doi.org/10.1515/crelle-2015-0023CrossRefGoogle Scholar
Cramér, H., Mathematical methods of statistics. Princeton Landmarks in Mathematics, Princeton, NJ, Princeton University Press, 1999. Reprint of the 1946 original.Google Scholar
Gruber, P. M., Convex and discrete geometry. Grundlehren der Mathematischen Wissenschaften, 336, Springer, Berlin, 2007.Google Scholar
Guleryuz, O. G., Lutwak, E., Yang, D., and Zhang, G., Information-theoretic inequalities for contoured probability distributions. IEEE Trans. Inform. Theory 48(2002), 2377–2383. https://doi.org/10.1109/TIT.2002.800496CrossRefGoogle Scholar
Haberl, C., Blaschke valuations. Amer. J. Math. 133(2011), 717–751. https://doi.org/10.1353/ajm.2011.0019CrossRefGoogle Scholar
Haberl, C., Minkowski valuations intertwining with the special linear group. J. Eur. Math. Soc. 14(2012), 1565–1597. https://doi.org/10.4171/JEMS/341CrossRefGoogle Scholar
Haberl, C. and Ludwig, M., A characterization of L p intersection bodies. Int. Math. Res. Not. 2006 Art. ID 10548, 29 pages. https://doi.org/10.1155/IMRN/2006/10548Google Scholar
Haberl, C. and Parapatits, L., The centro-affine Hadwiger theorem. J. Amer. Math. Soc. 27(2014), 685–705. https://doi.org/10.1090/S0894-0347-2014-00781-5CrossRefGoogle Scholar
Haberl, C. and Parapatits, L., Valuations and surface area measures. J. Reine Angew. Math. 687(2014), 225–245. https://doi.org/10.1515/crelle-2012-0044Google Scholar
Haberl, C. and Parapatits, L., Moments and valuations. Amer. J. Math. 138(2016), 1575–1603. https://doi.org/10.1353/ajm.2016.0047CrossRefGoogle Scholar
Haberl, C. and Parapatits, L., Centro-affine tensor valuations. Adv. Math. 316(2017), 806–865. https://doi.org/10.1016/j.aim.2017.06.030CrossRefGoogle Scholar
Hadwiger, H., Vorlesungen über Inhalt, Oberfläche und Isoperimetrie. Springer, Berlin, 1957.CrossRefGoogle Scholar
Hug, D. and Schneider, R., Local tensor valuations. Geom. Funct. Anal. 24(2014), 1516–1564. https://doi.org/10.1007/s00039-014-0289-0CrossRefGoogle Scholar
Hug, D., Schneider, R., and Schuster, R., Integral geometry of tensor valuations. Adv. Appl. Math. 41(2008), 482–509. https://doi.org/10.1016/j.aam.2008.04.001CrossRefGoogle Scholar
John, F., Extremum problems with inequalities as subsidiary conditions. In: Studies and essays presented to R. Courant on his 60th Birthday. Interscience Publishers, Inc., New York, 1948, pp. 187–204.Google Scholar
Klain, D. A., Star valuations and dual mixed volumes. Adv. Math. 121(1996), 80–101. https://doi.org/10.1006/aima.1996.0048CrossRefGoogle Scholar
Klain, D. A. and Rota, G. C., Introduction to geometric probability. Cambridge University Press, Cambridge, 1997.Google Scholar
Li, J. and Leng, G., L p Minkowski valuations on polytopes. Adv. Math. 299(2016), 139–173. https://doi.org/10.1016/j.aim.2016.05.009CrossRefGoogle Scholar
Li, J. and Ma, D., Laplace transforms and valuations. J. Funct. Anal. 272(2017), 738–758. https://doi.org/10.1016/j.jfa.2016.09.011CrossRefGoogle Scholar
Li, J., Yuan, S., and Leng, G., L p-Blaschke valuations. Trans. Amer. Math. Soc. 367(2015), 3161–3187. https://doi.org/10.1090/S0002-9947-2015-06047-4CrossRefGoogle Scholar
Ludwig, M., Moment vectors of polytopes, IV International Conference in Stochastic Geometry, Convex Bodies, Empirical Measures and Applications to Engineering Science. Rend. Circ. Mat. Palermo (2) Suppl. 70(2002), 123–138.Google Scholar
Ludwig, M., Projection bodies and valuations. Adv. Math. 172(2002), 158–168. https://doi.org/10.1016/S0001-8708(02)00021-XCrossRefGoogle Scholar
Ludwig, M., Valuations on ploytopes containing the origin in their interiors. Adv. Math. 170(2002), 239–256. https://doi.org/10.1006/aima.2002.2077CrossRefGoogle Scholar
Ludwig, M., Ellipsoids and matrix-valued valuations. Duke Math. J. 119(2003), 159–188. https://doi.org/10.1215/S0012-7094-03-11915-8CrossRefGoogle Scholar
Ludwig, M., Minkowski valuations. Trans. Amer. Math. Soc. 357(2005), 4191–4213. https://doi.org/10.1090/S0002-9947-04-03666-9CrossRefGoogle Scholar
Ludwig, M., Intersection bodies and valuations. Amer. J. Math. 128(2006), 1409–1428.CrossRefGoogle Scholar
Ludwig, M., Minkowski areas and valuations. J. Differential Geom. 86(2010), 133–161.CrossRefGoogle Scholar
Ludwig, M., Fisher information and matrix-valued valuations. Adv. Math. 226(2011), 2700–2711. https://doi.org/10.1016/j.aim.2010.08.021CrossRefGoogle Scholar
Ludwig, M., Covariance matrices and valuations. Adv. Appl. Math. 51(2013), 359–366. https://doi.org/10.1016/j.aam.2012.12.003CrossRefGoogle Scholar
Ludwig, M. and Reitzner, M., A classification of SL(n) invariant valuations. Ann. of Math. 172(2010), 1219–1267. https://doi.org/10.4007/annals.2010.172.1223CrossRefGoogle Scholar
Ludwig, M. and Reitzner, M., SL (n) invariant valuations on polytopes. Discrete Comput. Geom. 57(2017), 571–581. https://doi.org/10.1007/s00454-016-9838-7CrossRefGoogle Scholar
Ludwig, M. and Silverstein, L., Tensor valuations on lattice polytopes. Adv. Math. 319(2017), 76–110. https://doi.org/10.1016/j.aim.2017.08.015CrossRefGoogle Scholar
Lutwak, E., Yang, D., and Zhang, G., A new ellipsoid associated with convex bodies. Duke. Math. J. 104(2000), 375–390. https://doi.org/10.1215/S0012-7094-00-10432-2Google Scholar
Lutwak, E., Yang, D., and Zhang, G., The Cramer-Rao inequality for star bodies. Duke Math. J. 112(2002), 59–81. https://doi.org/10.1215/S0012-9074-02-11212-5Google Scholar
Lutwak, E., Yang, D., and Zhang, G., L p John ellipsoids. Proc. London Math. Soc. (3) 90(2005), 497–520. https://doi.org/10.1112/S0024611504014996CrossRefGoogle Scholar
Ma, D., Moment matrices and SL (n) equivariant valuations on polytopes. Int. Math. Res. Not.. https://doi.org/10.1093/imrn/rnz137Google Scholar
Parapatits, L., SL (n)-contravariant L p-Minkowski valuations. Trans. Amer. Math. Soc. 366(2014), 1195–1211. https://doi.org/10.1090/S0002-9947-2013-05750-9CrossRefGoogle Scholar
Parapatits, L., SL (n)-covariant L p-Minkowski valuations. J. London Math. Soc. 89(2014), 397–414. https://doi.org/10.1112/jlms/jdt068CrossRefGoogle Scholar
Pisier, G., The volume of convex bodies and Banach space geometry. Cambridge Tracts in Mathematics, 94, Cambridge University Press, Cambridge, 1989.CrossRefGoogle Scholar
Rao, C. R., Information and the accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 37(1945), 81–91.Google Scholar
Schneider, R., Convex bodies: the Brunn-Minkowski theory. Second expanded ed, Cambridge University Press, Cambridge, 2014.Google Scholar
Schuster, F. E. and Wannerer, T., GL (n) contravariant Minkowski valuations. Trans. Amer. Math. Soc. 364(2012), 815–826. https://doi.org/10.1090/S0002-9947-2011-05364-XCrossRefGoogle Scholar
Wannerer, T., GL (n) equivariant Minkowski valuations. Indiana Univ. Math. J. 60(2011), 1655–1672. https://doi.org/10.1512/iumj.2011.60.4425CrossRefGoogle Scholar
Zeng, C. and Ma, D., SL (n) covariant vector valuations on ploytopes. Trans. Amer. Math. Soc. 370(2018), 8999–9023. https://doi.org/10.1090/tran/7468CrossRefGoogle Scholar
Zou, D. and Xiong, G., Orlicz-John ellipsoids. Adv. Math. 265(2014), 132–168. https://doi.org/10.1016/j.aim.2014.07.034CrossRefGoogle Scholar