Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T15:41:48.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Holomorphic SCFTs with small index

Part of: Homology and cohomology theories Lie algebras and Lie superalgebras General mathematical topics and methods in quantum theory Theory of error-correcting codes and error-detecting codes

Published online by Cambridge University Press:  18 January 2021

Davide Gaiotto  and
Theo Johnson-Freyd
Davide Gaiotto*
Affiliation:
Perimeter Institute for Theoretical Physics, Waterloo, Ontario
Theo Johnson-Freyd
Affiliation:
Department of Mathematics and Statistics, Dalhousie University, Halifax, Nova Scotia e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

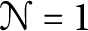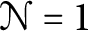We observe that every self-dual ternary code determines a holomorphic $\mathcal N=1$ superconformal field theory. This provides ternary constructions of some well-known holomorphic $\mathcal N=1$ superconformal field theories (SCFTs), including Duncan’s “supermoonshine” model and the fermionic “beauty and the beast” model of Dixon, Ginsparg, and Harvey. Along the way, we clarify some issues related to orbifolds of fermionic holomorphic CFTs. We give a simple coding-theoretic description of the supersymmetric index and conjecture that for every self-dual ternary code this index is divisible by $24$ ; we are able to prove this conjecture except in the case when the code has length 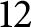$12$ mod $24$ . Lastly, we discuss a conjecture of Stolz and Teichner relating 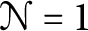$\mathcal N=1$ SCFTs with Topological Modular Forms. 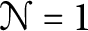This conjecture implies constraints on the supersymmetric indexes of arbitrary holomorphic SCFTs, and suggests (but does not require) that there should be, for each k, a holomorphic $\mathcal N=1$ SCFT of central charge 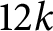$12k$ and index 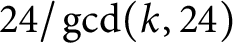$24/\gcd (k,24)$ . We give ternary code constructions of SCFTs realizing this suggestion for 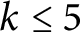$k\leq 5$ .

Keywords

Supersymmetryvertex operator algebraslinear codesmoonshineTMF

MSC classification

Primary: 17B69: Vertex operators; vertex operator algebras and related structures
Secondary: 94B05: Linear codes, general 81Q60: Supersymmetry and quantum mechanics 55N20: Generalized (extraordinary) homology and cohomology theories
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 2 , April 2022 , pp. 573 - 601
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We thank Noam D. Elkies for many valuable conversations, some of which were hosted by mathoverflow.net, and for helping with a number of calculations. We also thank Greg Moore, Jeff Harvey, and an anonymous referee for comments on a draft of this paper. Research at the Perimeter Institute for Theoretical Physics is supported by the Government of Canada through the Department of Innovation, Science and Economic Development Canada and by the Province of Ontario through the Ministry of Research, Innovation and Science.

References

Bhardwaj, L., Gaiotto, D., and Kapustin, A., State sum constructions of spin-TFTs and string net constructions of fermionic phases of matter . J. High Energy Phys. 96(2017). https://doi.org/10.1007/JHEP04(2017)096Google Scholar
Borcherds, R. E., Automorphic forms on ${O}_{s+2,2}(R)$ and infinite products . Invent. Math. 120(1995), no. 1, 161–213. https://doi.org/10.1007/BF01241126 CrossRefGoogle Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A., and Wilson, R. A., Atlas of finite groups. Oxford University Press, Eynsham, 1985. Maximal subgroups and ordinary characters for simple groups, with computational assistance from Thackray, J. G..Google Scholar
Cheng, M. C. N., Dong, X., Duncan, J. F. R., Harrison, S., Kachru, S., and Wrase, T., Mock modular Mathieu moonshine modules . Res. Math. Sci. 2(2015), Art. 13, 89. https://doi.org/10.1186/s40687-015-0034-9 CrossRefGoogle Scholar
Creutzig, T., Kanade, S., and McRae, R., Tensor categories for vertex operator superalgebra extensions. Preprint, 2017. arXiv:1705.05017 Google Scholar
Carnahan, S. and Miyamoto, M., Regularity of fixed-point vertex operator subalgebras. Preprint, 2016. arXiv:1603.05645 Google Scholar
Conway, J. H. and Norton, S. P., Monstrous moonshine . Bull. Lond. Math. Soc. 11(1979), no. 3, 308–339. https://doi.org/10.1112/blms/11.3.308 CrossRefGoogle Scholar
Conway, J. H. and Sloane, N. J. A., Sphere packings, lattices and groups , Vol. 290, 3rd ed., Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Springer-Verlag, New York, 1999. With additional contributions by Bannai, E., Borcherds, R. E., Leech, J., Norton, S. P., Odlyzko, A. M., Parker, R. A., Queen, L., and Venkov, B. B..Google Scholar
Douglas, C. L., Francis, J., Henriques, A. G., and Hill, M. A. (eds.), Topological modular forms, Mathematical Surveys and Monographs, 201, American Mathematical Society, Providence, RI, 2014.CrossRefGoogle Scholar
Dixon, L., Ginsparg, P., and Harvey, J., Beauty and the beast: superconformal symmetry in a Monster module . Comm. Math. Phys. 119 (1988), no. 2, 221–241.CrossRefGoogle Scholar
Dong, C., Vertex algebras associated with even lattices . J. Algebra 161(1993), no. 1, 245–265. https://doi.org/10.1006/jabr.1993.1217 CrossRefGoogle Scholar
Dong, C. and Nagatomo, K., Automorphism groups and twisted modules for lattice vertex operator algebras . In: Recent developments in quantum affine algebras and related topics (Raleigh, NC, 1998), Contemporary Mathematics, 248, American Mathematical Society, Providence, RI, 1999, pp. 117–133. arXiv:math/9808088 https://doi.org/10.1090/conm/248/03821 CrossRefGoogle Scholar
Duncan, J. F., Super-moonshine for Conway’s largest sporadic group . Duke Math. J. 139 (2007), no. 2, 255–315. https://doi.org/10.1215/S0012-7094-07-13922-X arXiv:math/0502267 CrossRefGoogle Scholar
Dijkgraaf, R., Vafa, C., Verlinde, E., and Verlinde, H., The operator algebra of orbifold models . Comm. Math. Phys. 123(1989), no. 3, 485–526.CrossRefGoogle Scholar
Elkies, N. D., Lattices, linear codes, and invariants. II. Notices . Amer. Math. Soc. 47(2000), no. 11, 1382–1391.Google Scholar
Frenkel, E. and Ben-Zvi, D., Vertex algebras and algebraic curves , Vol. 88, 2nd ed., Mathematical Surveys and Monographs, American Mathematical Society, Providence, RI, 2004. https://doi.org/10.1090/surv/088 Google Scholar
Frenkel, I., Lepowsky, J., and Meurman, A., Vertex operator algebras and the Monster , Vol. 134. Pure and Applied Mathematics, Academic Press, Inc., Boston, MA, 1988.Google Scholar
Frame, J. S., The characters of the Weyl group E8 . In: Computational problems in abstract algebra, Proc. Conf., Oxford, 1967, Pergamon, Oxford, 1970, pp. 111–130.Google Scholar
Freed, D. S., Pions and generalized cohomology . J. Differ. Geom. 80(2008), no. 1, 45–77. arXiv:hep-th/0607134 CrossRefGoogle Scholar
Freed, D. S. and Teleman, C., Relative quantum field theory . Comm. Math. Phys. 326(2014), no. 2, 459–476. https://doi.org/10.1007/s00220-013-1880-1. arXiv:1212.1692 CrossRefGoogle Scholar
Gaberdiel, M. R., Persson, D., Ronellenfitsch, H., and Volpato, R., Generalized Mathieu Moonshine . Commun. Number Theor. Phys. 7(2013), no. 1, 145–223. https://doi.org/10.4310/CNTP.2013.v7.n1.a5. arXiv:1211.7074 CrossRefGoogle Scholar
Gaiotto, D. and Johnson-Freyd, T., Symmetry protected topological phases and generalized cohomology . J. High Energy Phys. 34(2019), no. 5, 7. https://doi.org/10.1007/JHEP05(2019)007. arXiv:1712.07950 CrossRefGoogle Scholar
Goddard, P. and Olive, D., Kac-Moody algebras, conformal symmetry and critical exponents . Nuclear Phys. B 257(1985), no. 2, 226–252. https://doi.org/10.1016/0550-3213(85)90344-X CrossRefGoogle Scholar
Golay, M., Notes on digital coding. Proc. Inst. Radio Eng. (1949), p. 657.Google Scholar
Gu, Z.-C. and Wen, X.-G., Symmetry-protected topological orders for interacting fermions: Fermionic topological nonlinear sigma models and a special group supercohomology theory . Phys. Rev. B90(2014), no. 11, 115141. https://doi.org/10.1103/PhysRevB.90.115141. arXiv:1201.2648 CrossRefGoogle Scholar
Harada, M. and Munemasa, A., A complete classification of ternary self-dual codes of length 24 . J. Combin. Theory Ser. A 116(2009), no. 5, 1063–1072. https://doi.org/10.1016/j.jcta.2008.11.011. arXiv:0804.0637 CrossRefGoogle Scholar
Heluani, R. and Kac, G. V., Susy lattice vertex algebras. Preprint, 2007. arXiv:0710.1587 CrossRefGoogle Scholar
Hopkins, M. J., Algebraic topology and modular forms . In: Proc. Int. Congr. Math., Vol. I (Beijing, 2002), Higher Ed. Press, Beijing, 2002, pp. 291–317. arXiv:math/0212397 Google Scholar
Kac, V., Vertex algebras for beginners , Vol. 10. 2nd ed., University Lecture Series, American Mathematical Society, Providence, RI, 1998. https://doi.org/10.1090/ulect/010 CrossRefGoogle Scholar
Kirillov, A. Jr., Modular categories and orbifold models . Comm. Math. Phys. 229(2002), no. 2, 309–335. https://doi.org/10.1007/s002200200650. arXiv:math/0104242 CrossRefGoogle Scholar
Kock, A., Kristensen, L., and Madsen, I., Cochain functors for general cohomology theories I, II . Math. Scand. 20(1967), nos. 131–150, 151–176.CrossRefGoogle Scholar
Leon, J. S., Pless, V., and Sloane, N. J. A., On ternary self-dual codes of length 24 . IEEE Trans. Inform. Theor. 27(1981), no. 2, 176–180. https://doi.org/10.1109/TIT.1981.1056328 CrossRefGoogle Scholar
Lepowsky, J., Calculus of twisted vertex operators . Proc. Nat. Acad. Sci. USA 82(1985), no. 24, 8295–8299. https://doi.org/10.1073/pnas.82.24.8295 CrossRefGoogle ScholarPubMed
Li, H. S. and Xu, X., A characterization of vertex algebras associated to even lattices . J. Algebra 173(1995), no. 2, 253–270. https://doi.org/10.1006/jabr.1995.1087 CrossRefGoogle Scholar
Möller, S., A cyclic orbifold theory for holomorphic vertex operator algebras and applications. Ph.D. thesis, Technische Universität Darmstadt, 2016. arXiv:1611.09843 Google Scholar
Müger, M., On superselection theory of quantum fields in low dimensions . In: XVIth International Congress on Mathematical Physics, World Scientific Publications, Hackensack, NJ, 2010, pp. 496–503. https://doi.org/10.1142/9789814304634_0041 CrossRefGoogle Scholar
O’Connor, R. E. and Pall, G., The construction of integral quadratic forms of determinant 1 . Duke Math. J. 11(1944), 319–331.CrossRefGoogle Scholar
Pless, V., On a new family of symmetry codes and related new five-designs . Bull. Amer. Math. Soc. 75(1969), 1339–1342. https://doi.org/10.1090/S0002-9904-1969-12418-3 CrossRefGoogle Scholar
Schellekens, A. N., Meromorphic $c=24$ conformal field theories. Comm. Math. Phys. 153(1993), no. 1, 159–185.Google Scholar
Segal, G., Elliptic cohomology (after Landweber-Stong, Ochanine, Witten, and others) . Astérisque 4(1988, 1989), no. 695, 187–201. Séminaire Bourbaki, Vol. 1987/88.Google Scholar
Stolz, S. and Teichner, P., What is an elliptic object? In: Topology, geometry and quantum field theory, London Mathematical Society Lecture Note Series, 308, Cambridge University Press, Cambridge, 2004, pp. 247–343. https://doi.org/10.1017/CBO9780511526398.013 CrossRefGoogle Scholar
Stolz, S. and Teichner, P., Supersymmetric field theories and generalized cohomology . In: Mathematical foundations of quantum field theory and perturbative string theory, Proc. Sympos. Pure Math., 83, American Mathematical Society, Providence, RI, 2011, pp. 279–340. arXiv:1108.0189 CrossRefGoogle Scholar
Wang, Q.-R. and Gu, Z.-C., Towards a complete classification of symmetry-protected topological phases for interacting fermions in three dimensions and a general group supercohomology theory . Phys. Rev. 8(2018), 011055. https://doi.org/10.1103/PhysRevX.8.011055. arXiv:1703.10937 CrossRefGoogle Scholar
Witten, E., Elliptic genera and quantum field theory . Comm. Math. Phys. 109(1987), no. 4, 525–536.CrossRefGoogle Scholar
Witten, E., The index of the Dirac operator in loop space . In: Elliptic curves and modular forms in algebraic topology (Princeton, NJ, 1986), Lecture Notes in Mathematics, 1326, Springer, Berlin, 1988, pp. 161–181. https://doi.org/10.1007/BFb0078045 CrossRefGoogle Scholar