Published online by Cambridge University Press: 07 March 2019
The second eigenvalue of the Robin Laplacian is shown to be maximal for the disk among simply-connected planar domains of fixed area when the Robin parameter is scaled by perimeter in the form 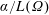 $\unicode[STIX]{x1D6FC}/L(\unicode[STIX]{x1D6FA})$, and
$\unicode[STIX]{x1D6FC}/L(\unicode[STIX]{x1D6FA})$, and  $\unicode[STIX]{x1D6FC}$ lies between
$\unicode[STIX]{x1D6FC}$ lies between 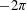 $-2\unicode[STIX]{x1D70B}$ and
$-2\unicode[STIX]{x1D70B}$ and 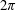 $2\unicode[STIX]{x1D70B}$. Corollaries include Szegő’s sharp upper bound on the second eigenvalue of the Neumann Laplacian under area normalization, and Weinstock’s inequality for the first nonzero Steklov eigenvalue for simply-connected domains of given perimeter.
$2\unicode[STIX]{x1D70B}$. Corollaries include Szegő’s sharp upper bound on the second eigenvalue of the Neumann Laplacian under area normalization, and Weinstock’s inequality for the first nonzero Steklov eigenvalue for simply-connected domains of given perimeter.
The first Robin eigenvalue is maximal, under the same conditions, for the degenerate rectangle. When area normalization on the domain is changed to conformal mapping normalization and the Robin parameter is positive, the maximiser of the first eigenvalue changes back to the disk.
This research was supported by the Fundação para a Ciência e a Tecnologia (Portugal) through project PTDC/MAT-CAL/4334/2014 (Pedro Freitas), by a grant from the Simons Foundation (#429422 to Richard Laugesen), by travel support for Laugesen from the American Institute of Mathematics to the workshop on Steklov Eigenproblems (April–May 2018), and support from the University of Illinois Scholars’ Travel Fund.