Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T02:31:04.127Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimension groups for self-similar maps and matrix representations of the cores of the associated C*-algebras

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  12 May 2020

Tsuyoshi Kajiwara  and
Yasuo Watatani
Tsuyoshi Kajiwara*
Affiliation:
Department of Environmental and Mathematical Sciences, Okayama University, Tsushima, Okayama, 700-8530, Japan
Yasuo Watatani
Affiliation:
Department of Mathematical Sciences, Kyushu University, Motooka, Fukuoka, 819-0395, Japan e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a dimension group for a self-similar map as the 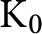$\mathrm {K}_0$ -group of the core of the C*-algebra associated with the self-similar map together with the canonical endomorphism. The key step for the computation is an explicit description of the core as the inductive limit using their matrix representations over the coefficient algebra, which can be described explicitly by the singularity structure of branched points. We compute that the dimension group for the tent map is isomorphic to the countably generated free abelian group 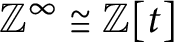${\mathbb Z}^{\infty }\cong {\mathbb Z}[t]$ together with the unilateral shift, i.e. the multiplication map by t as an abstract group. 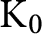Thus the canonical endomorphisms on the $\mathrm {K}_0$ -groups are not automorphisms in general. This is a different point compared with dimension groups for topological Markov shifts. We can count the singularity structure in the dimension groups.

Keywords

Self-similar mapcoredimension group

MSC classification

Primary: 46L80: $K$-theory and operator algebras (including cyclic theory)
Secondary: 46L08: $C^*$-modules 46L35: Classifications of $C^*$-algebras 46L55: Noncommutative dynamical systems
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 4 , August 2021 , pp. 1013 - 1056
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Castro, G., C*-algebras associated with iterated function systems . Contemp. Math. 503(2010), 27–38.CrossRefGoogle Scholar
Cuntz, J. and Krieger, W., A class of ${C}^{\ast }$ -algebras and topological Markov chains . Invent. Math. 56(1980), 251–268.CrossRefGoogle Scholar
Deaconu, V. and Shultz, F., C*-algebras associated with interval maps . Trans. Amer. Math. Soc. 359(2007), 1889–1924.CrossRefGoogle Scholar
Falconer, K. J., Fractal geometry . Wiley, Hoboken, NJ, 1997.Google Scholar
Jeong, J., Saturated actions by finite-dimensional Hopf*-algebras on ${C}^{\ast }$ -algebras . Int. J. Math. 19(2008), 125–144.CrossRefGoogle Scholar
Kajiwara, T. and Watatani, Y., C* algebras associated with self-similar maps . J. Oper. Theory 56(2006), 225–247.Google Scholar
Kajiwara, T. and Watatani, Y., Traces on core of the C*-algebras constructed from self-similar maps . Ergod. Theory Dyn. Sys. 34(2014), 1964–1989.CrossRefGoogle Scholar
Kajiwara, T. and Watatani, Y., Ideals of the core of C*-algebras associated with self-similar maps . J. Oper. Theory 75(2016), 1225–1255.Google Scholar
Kajiwara, T. and Watatani, Y., Maximal abelian subalgebras of ${C}^{\ast }$ -algebras associated with complex dynamical systems and self-similar maps . J. Math. Anal. Appl. 455(2017), 1383–1400.CrossRefGoogle Scholar
Kigami, J., Analysis on fractals . Cambridge University Press, Cambridge, MA, 2001.CrossRefGoogle Scholar
Krieger, W., On dimension for a class of homeomorphism groups . Math. Ann. 252(1980), 87–95.CrossRefGoogle Scholar
Krieger, W., On dimension functions and topological Markov chains . Invent. Math. 56(1980), 239–250.CrossRefGoogle Scholar
Matsumoto, K., On C*-algebras associated with subshifts . Int. J. Math. 8(1997), 357–374.CrossRefGoogle Scholar
Matsumoto, K., K-theory for C*-algebras associated with subshifts . Math. Scand. 82(1998), 237–255.CrossRefGoogle Scholar
Phillips, C., Equivariant K-theory and freeness of group actions on C*-algebra. Lecture Notes in Mathematics, 1274, Springer-Verlag, Berlin, Germany, 1987.CrossRefGoogle Scholar
Pimsner, M., A class of C*-algebras generating both Cuntz-Krieger algebras and crossed product by $\,\mathbb{Z}$ Free probability theory . Free Probabil. Theory AMS 12(1997), 189–212.Google Scholar
Rordam, M., Larsen, F., and Laustsen, N. J., An introduction to K-theory for C*-algebras. Mathematical Society, Student Texts, 49, London, UK, 2000, p. 256.Google Scholar
Rosenberg, J., Appendix to O. Bratteli’s paper on crossed products of UHF algebras . Duke Math. J. 46(1979), 25–26.CrossRefGoogle Scholar
Shultz, F., Dimension groups for interval maps. New York J. Math. 11(2005), 477–517.Google Scholar
Shultz, F., Dimension groups for inteval maps II . Ergod. Theory Dynam. Sys. 27(2017), 1287–1321.CrossRefGoogle Scholar