Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T14:48:52.544Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorics of the geometry of Wilson loop diagrams II: Grassmann necklaces, dimensions, and denominators

Part of: Quantum field theory; related classical field theories

Published online by Cambridge University Press:  23 July 2021

Susama Agarwala ,
Siân Fryer  and
Karen Yeats
Susama Agarwala
Affiliation:
Applied Physics Laboratory, Johns Hopkins University, Laurel, MD, USA e-mail: [email protected]
Siân Fryer
Affiliation:
UC Santa Barbara, Department of Mathematics Yeats, Santa Barbara, CA, USA e-mail: [email protected]
Karen Yeats*
Affiliation:
University of Waterloo, Department of Combinatorics and Optimization, Waterloo, ON, Canada
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Wilson loop diagrams are an important tool in studying scattering amplitudes of SYM 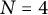$N=4$ theory and are known by previous work to be associated to positroids. In this paper, we study the structure of the associated positroids, as well as the structure of the denominator of the integrand defined by each diagram. We give an algorithm to derive the Grassmann necklace of the associated positroid directly from the Wilson loop diagram, and a recursive proof that the dimension of these cells is thrice the number of propagators in the diagram. We also show that the ideal generated by the denominator in the integrand is the radical of the ideal generated by the product of Grassmann necklace minors.

Keywords

Wilson loop diagramspositroidsGrassmann necklaceLe diagram

MSC classification

Primary: 81T60: Supersymmetric field theories
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 6 , December 2022 , pp. 1625 - 1672
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

SA was partially supported by an Office of Naval Research grant. KY is supported by an NSERC Discovery grant, by the Canada Research Chair Program, and also, through some the time this work was developed, by a Humboldt Fellowship from the Alexander von Humboldt Foundation.

References

Adamo, T., Bullimore, M., Mason, L., and Skinner, D., Scattering amplitudes and Wilson loops in twistor space . J. Phys. A 44(2011), no. 45, 454008.CrossRefGoogle Scholar
Adamo, T. and Mason, L., MHV diagrams in twistor space and the twistor action . Phys. Rev. D 86(2011), 065019.CrossRefGoogle Scholar
Adamo, T. and Mason, L., Twistor-strings and gravity tree amplitudes . Classical Quantum Gravity 30(2013), no. 7, 075020.CrossRefGoogle Scholar
Agarwala, S. and Fryer, S., An algorithm to construct the Le diagram associated to a Grassmann necklace . Glasg. Math. J. 62(2020), no. 1, 85–91.CrossRefGoogle Scholar
Agarwala, S. and Fryer, S., A study in ${Gr}_{\ge 0}\left(2,6\right)$ : from the geometric case book of Wilson loop diagrams and SYM $N=4$ . Preprint, 2018. https://www.ems-ph.org/journals/forthcoming.php?jrn=aihpd Google Scholar
Agarwala, S., Fryer, S., and Yeats, K., Combinatorics of the geometry of Wilson loop diagrams I: Equivalence classes via matroids and polytopes. Canadian Journal of Mathematics. (2021), 1–32. https://doi.org/10.4153/S0008414X21000134 CrossRefGoogle Scholar
Agarwala, S. and Marcott, C., Wilson loops in SYM $N=4$ do not parametrize an orientable space. Preprint, 2018. arXiv:1807.05397 Google Scholar
Agarwala, S. and Marin-Amat, E., Wilson loop diagrams and positroids . Comm. Math. Phys. 350(2017), no. 2, 569–601.CrossRefGoogle Scholar
Alday, L. F. and Maldacena, J. M., Gluon scattering amplitudes at strong coupling . J. High Energy Phys. 706(2007), 64.CrossRefGoogle Scholar
Arkani-Hamed, N., Bourjaily, J., Cachazo, F., Goncharov, A., Postnikov, A., and Trnka, J., Grassmannian geometry of scattering amplitudes, Cambridge University Press, Cambridge, 2016.CrossRefGoogle Scholar
Arkani-Hamed, N., Thomas, H., and Trnka, J., Unwinding the amplituhedron in binary . J. High Energy Phys. 2018(2018), no. 1, 16, front matter + 40.CrossRefGoogle Scholar
Arkani-Hamed, N. and Trnka, J., Into the Amplituhedron . J. High Energy Phys. 12(2014), 182.CrossRefGoogle Scholar
Arkani-Hamed, N. and Trnka, J., The Amplituhedron . J. High Energy Phys. 10(2014), 30.CrossRefGoogle Scholar
Boels, R., Mason, L., and Skinner, D., From twistor actions to MHV diagrams . Phys. Lett. B. 648(2007), no. 1, 90–96.CrossRefGoogle Scholar
Britto, R., Cachazo, F., Feng, B., and Witten, E., Direct proof of the tree-level scattering amplitude recursion relation in Yang–Mills theory . Phys. Rev. Lett. 94(2005), no. 18, 181602.CrossRefGoogle ScholarPubMed
Bullimore, M., Mason, L., and Skinner, D., MHV diagrams in momentum twistor space . J. High Energy Phys. 2010(2010), no. 12, 32.CrossRefGoogle Scholar
Cachazo, F., Svrcek, P., and Witten, E., MHV vertices in tree amplitudes in gauge theory . J. High Energy Phys. 9(2004), 6.CrossRefGoogle Scholar
Casteels, K., Quantum matrices by paths . Algebra Number Theory 8(2014), no. 8, 1857–1912.CrossRefGoogle Scholar
Chavez, A. and Gotti, F., Dyck paths and positroids from unit interval orders . J. Combin. Theory Ser. A 154(2018), 507–532.CrossRefGoogle Scholar
Eden, B., Heslop, P., and Mason, L., The correlahedron . J. High Energy Phys. 2017(2017), no. 9, 156, front matter + 40.CrossRefGoogle Scholar
Galashin, P. and Lam, T., Parity duality for the amplituhedron. Compositio Mathematica. 156(2020), no. 11, 2207–2262. https://doi.org/10.1112/S0010437X20007411 CrossRefGoogle Scholar
Gale, D., Optimal assignments in an ordered set: an application of matroid theory . J. Combin. Theory 4(1968), 176–180.CrossRefGoogle Scholar
Heslop, P. and Stewart, A., The twistor Wilson loop and the amplituhedron . J. High Energy Phys. 2018(2018), no. 10, 142, front matter + 18.CrossRefGoogle Scholar
Hodges, A., Eliminating spurious poles from gauge-theoretic amplitudes . J. High Energy Phys. 2013(2013), no. 5, 135.CrossRefGoogle Scholar
Karp, S. N., Williams, L., and Zhang, Y. X., Decompostions of amplituhedra. Ann. Inst. Henri Poincaré Comb. Phys. Interact. 7(2020), 303–363. https://doi.org/10.4171/AIHPD/87 CrossRefGoogle Scholar
Lipstein, A. E. and Mason, L., From the holomorphic Wilson loop to “d log” loop-integrands for super-Yang–Mills amplitudes . J. High Energy Phys. 5(2013), 106.CrossRefGoogle Scholar
Marcott, C., Basis shape loci and the positive Grassmannian. Preprint, 2019. arXiv:1904.13361 Google Scholar
Parke, S. and Taylor, T., Amplitude for n-gluon scattering . Phys. Rev. Lett. 56(1986), 2459.CrossRefGoogle ScholarPubMed
Positroids, S. O., Schubert matroids . J. Combin. Theory Ser. A 118(2011), no. 8, 2426–2435.Google Scholar
Postnikov, A., Total positivity, Grassmannians, and networks. Preprint, 2006. arXiv:math/0609764 Google Scholar