Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T21:17:51.481Z Has data issue: false hasContentIssue false
  • English
  • Français

Automatic Sequences and Generalised Polynomials

Part of: Diophantine approximation, transcendental number theory Topological dynamics Sequences and sets Graph theory Ergodic theory

Published online by Cambridge University Press:  13 June 2019

Jakub Byszewski  and
Jakub Konieczny
Jakub Byszewski
Affiliation:
Department of Mathematics and Computer Science, Institute of Mathematics, Jagiellonian University, ul. prof. Stanisława Łojasiewicza 6, 30-348 Kraków Email: [email protected]
Jakub Konieczny
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, Oxford, OX2 6GG
Get access Rights & Permissions [Opens in a new window]

Abstract

We conjecture that bounded generalised polynomial functions cannot be generated by finite automata, except for the trivial case when they are ultimately periodic.

Using methods from ergodic theory, we are able to partially resolve this conjecture, proving that any hypothetical counterexample is periodic away from a very sparse and structured set. In particular, we show that for a polynomial 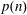$p(n)$ with at least one irrational coefficient (except for the constant one) and integer 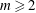$m\geqslant 2$, the sequence 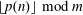$\lfloor p(n)\rfloor \hspace{0.2em}{\rm mod}\hspace{0.2em}m$ is never automatic.

We also prove that the conjecture is equivalent to the claim that the set of powers of an integer 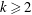$k\geqslant 2$ is not given by a generalised polynomial.

Keywords

generalised polynomialautomatic sequenceIP setnilmanifoldlinear recurrence sequenceregular sequence

MSC classification

Primary: 11B85: Automata sequences
Secondary: 37A45: Relations with number theory and harmonic analysis 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 37B10: Symbolic dynamics 11J71: Distribution modulo one 11B37: Recurrences 05C20: Directed graphs (digraphs), tournaments
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 2 , April 2020 , pp. 392 - 426
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Einstein Institute of Mathematics, Edmond J. Safra Campus, The Hebrew University of Jerusalem, Givat Ram, Jerusalem, 9190401, Israel Email: [email protected]

This research was supported by the National Science Centre, Poland (NCN) under grant no. DEC-2012/07/E/ST1/00185.

References

Adamczewski, B. and Bell, J., Function fields in positive characteristic: expansions and Cobham’s theorem. J. Algebra 319(2008), 2337–2350. https://doi.org/10.1016/j.jalgebra.2007.06.039.Google Scholar
Adamczewski, B. and Bell, J. P., On vanishing coefficients of algebraic power series over fields of positive characteristic. Invent. Math. 187(2012), 343–393. https://doi.org/10.1007/s00222-011-0337-4.Google Scholar
Allouche, J.-P. and Shallit, J., The ring of k-regular sequences. Theoret. Comput. Sci. 98(1992), 163–197. https://doi.org/10.1016/0304-3975(92)90001-V.Google Scholar
Allouche, J.-P. and Shallit, J., Automatic sequences. Theory, applications, generalizations. Cambridge University Press, Cambridge, 2003. https://doi.org/10.1017/CBO9780511546563.Google Scholar
Allouche, J.-P. and Shallit, J., The ring of k-regular sequences. II. Theoret. Comput. Sci. 307(2003), 3–29. https://doi.org/10.1016/S0304-3975(03)00090-2.Google Scholar
Baum, L. E. and Sweet, M. M., Continued fractions of algebraic power series in characteristic 2. Ann. of Math. (2) 103(1976), 593–610. https://doi.org/10.2307/1970953.Google Scholar
Bell, J. P., p-adic valuations and k-regular sequences. Discrete Math. 307(2007), 3070–3075. https://doi.org/10.1016/j.disc.2007.03.009.Google Scholar
Bell, J., Hare, K., and Shallit, J., When is an automatic set an additive basis? Proc. Amer. Math. Soc. Ser. B 5(2018), 50–63. https://doi.org/10.1090/bproc/37.Google Scholar
Bergelson, V. and Leibman, A., Distribution of values of bounded generalized polynomials. Acta Math. 198(2007), 155–230. https://doi.org/10.1007/s11511-007-0015-y.Google Scholar
Bergelson, V. and Leibman, A., Sets of large values of correlation functions for polynomial cubic configurations. Ergodic Theory Dynam. Systems 38(2018), 499–522. https://doi.org/10.1017/etds.2016.49.Google Scholar
Berstel, J., Mots de Fibonacci. In: Séminaire d’Informatique Théorique, Paris. 1980–1981, pp. 57–78.Google Scholar
Berstel, J., Fibonacci words, a survey. In: The Book of L. Springer-Verlag, 1985, pp. 11–25.Google Scholar
Berstel, J. and Séébold, P., A characterization of Sturmian morphisms. In: Mathematical foundations of computer science 1993 (Gdańsk, 1993). Lecture Notes in Comput. Sci., 711, Springer, Berlin, 1993, pp. 281–290. https://doi.org/10.1007/3-540-57182-5_20.Google Scholar
Berthé, V., Ei, H., Ito, S., and Rao, H., On substitution invariant Sturmian words: an application of Rauzy fractals. Theor. Inform. Appl. 41(2007), 329–349. https://doi.org/10.1051/ita:2007026.Google Scholar
Byszewski, J. and Konieczny, J., Factors of generalised polynomials and automatic sequences. Indag. Math. (N.S.) 29(2018), 981–985. https://doi.org/10.1016/j.indag.2018.03.003.Google Scholar
Byszewski, J. and Konieczny, J., Sparse generalised polynomials. Trans. Amer. Math. Soc. 370(2018), 8081–8109. https://doi.org/10.1090/tran/7257.Google Scholar
Chomsky, N., On certain formal properties of grammars. Information and Control 2(1959), 137–167.Google Scholar
Cobham, A., On the base-dependence of sets of numbers recognizable by finite automata. Math. Systems Theory 3(1969), 186–192. https://doi.org/10.1007/BF01746527.Google Scholar
Cobham, A., Uniform tag sequences. Math. Systems Theory 6(1972), 164–192. https://doi.org/10.1007/BF01706087.Google Scholar
Derksen, H., A Skolem-Mahler-Lech theorem in positive characteristic and finite automata. Invent. Math. 168(2007), 175–224. https://doi.org/10.1007/s00222-006-0031-0.Google Scholar
Derksen, H. and Masser, D., Linear equations over multiplicative groups, recurrences, and mixing II. Indag. Math. (N.S.) 26(2015), 113–136. https://doi.org/10.1016/j.indag.2014.08.002.Google Scholar
Eilenberg, S., Automata, languages, and machines. Vol. A. Pure and Applied Mathematics, 58, Academic Press [A subsidiary of Harcourt Brace Jovanovich, Publishers], New York, 1974.Google Scholar
Einsiedler, M. and Ward, T., Ergodic theory with a view towards number theory. Graduate Texts in Mathematics, 259, Springer-Verlag London, Ltd., London, 2011. https://doi.org/10.1007/978-0-85729-021-2.Google Scholar
Everest, G., van der Poorten, A., Shparlinski, I., and Ward, T., Recurrence sequences. Mathematical Surveys and Monographs, 104, American Mathematical Society, Providence, RI, 2003. https://doi.org/10.1090/surv/104.Google Scholar
Evertse, J.-H., On sums of S-units and linear recurrences. Compositio Math. 53(1984), 225–244.Google Scholar
Fagnot, I., A little more about morphic Sturmian words. Theor. Inform. Appl. 40(2006), 511–518. https://doi.org/10.1051/ita:2006031.Google Scholar
Fan, A. and Konieczny, J., On uniformity of q-multiplicative sequences. Bull. Lond. Math. Soc. (2019). https://doi.org/10.1112/blms.12245.Google Scholar
Furstenberg, H., Strict ergodicity and transformation of the torus. Amer. J. Math. 83(1961), 573–601. https://doi.org/10.2307/2372899.Google Scholar
Furstenberg, H., Recurrence in ergodic theory and combinatorial number theory. M. B. Porter Lectures, Princeton University Press, Princeton, NJ, 1981.Google Scholar
Gawrychowski, P., Krieger, D., Rampersad, N., and Shallit, J., Finding the growth rate of a regular or conOtext-free language in polynomial time. Internat. J. Found. Comput. Sci. 21(2010), 597–618. https://doi.org/10.1142/S0129054110007441.Google Scholar
Gowers, W. T., A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11(2001), 465–588. https://doi.org/10.1007/s00039-001-0332-9.Google Scholar
Green, B. and Tao, T., An arithmetic regularity lemma, an associated counting lemma, and applications. In: An irregular mind. Bolyai Soc. Math. Stud., 21, János Bolyai Math. Soc., Budapest, 2010, pp. 261–334. https://doi.org/10.1007/978-3-642-14444-8_7.Google Scholar
Green, B. and Tao, T., The quantitative behaviour of polynomial orbits on nilmanifolds. Ann. of Math. (2) 175(2012), 465–540. https://doi.org/10.4007/annals.2012.175.2.2.Google Scholar
Green, B., Tao, T., and Ziegler, T., An inverse theorem for the Gowers U s+1[N]-norm. Ann. of Math. (2) 176(2012), 1231–1372. https://doi.org/10.4007/annals.2012.176.2.11.Google Scholar
Håland, I. J., Uniform distribution of generalized polynomials. J. Number Theory 45(1993), 327–366. https://doi.org/10.1006/jnth.1993.1082.Google Scholar
Håland, I. J., Uniform distribution of generalized polynomials of the product type. Acta Arith. 67(1994), 13–27. https://doi.org/10.4064/aa-67-1-13-27.Google Scholar
Håland, I. J. and Knuth, D. E., Polynomials involving the floor function. Math. Scand. 76(1995), 194–200. https://doi.org/10.7146/math.scand.a-12534.Google Scholar
Kedlaya, K. S., Finite automata and algebraic extensions of function fields. J. Théor. Nombres Bordeaux 18(2006), 379–420.Google Scholar
Kleene, S. C., Representation of events in nerve nets and finite automata. In: Automata studies. Annals of mathematics studies, 34, Princeton University Press, Princeton, N. J., 1956, pp. 3–41.Google Scholar
Konieczny, J., Gowers norms for the Thue–Morse and Rudin–Shapiro sequences. Annales de l’Institut Fourier, to appear. arxiv:1611.09985.Google Scholar
Kronecker, L., Zwei Sätze über Gleichungen mit ganzzahligen Coefficienten. J. Reine Angew. Math. 53(1857), 173–175.Google Scholar
Leibman, A., A canonical form and the distribution of values of generalized polynomials. Israel J. Math. 188(2012), 131–176. https://doi.org/10.1007/s11856-011-0097-2.Google Scholar
Lothaire, M., Algebraic combinatorics on words. Encyclopedia of Mathematics and its Applications, 90, Cambridge University Press, Cambridge, 2002.Google Scholar
Medina, L. A. and Rowland, E., p-regularity of the p-adic valuation of the Fibonacci sequence. Fibonacci Quart. 53(2015), 265–271.Google Scholar
Miller, J. S., Two notes on subshifts. Proc. Amer. Math. Soc. 140(2012), 1617–1622. https://doi.org/10.1090/S0002-9939-2011-11000-1.Google Scholar
Moosa, R. and Scanlon, T., The Mordell-Lang conjecture in positive characteristic revisited. In: Model theory and applications. Quad. Mat., 11, Aracne, Rome, 2002, pp. 273–296.Google Scholar
Moshe, Y., On some questions regarding k-regular and k-context-free sequences. Theoret. Comput. Sci. 400(2008), 62–69. 2008. https://doi.org/10.1016/j.tcs.2008.02.018.Google Scholar
Rigo, M., Generalization of automatic sequences for numeration systems on a regular language. Theoret. Comput. Sci. 244(2000), 271–281. https://doi.org/10.1016/S0304-3975(00)00163-8.Google Scholar
Rowland, E. S., Non-regularity of ⌊𝛼+logkn⌋. Integers 10(2010), A3, 19–23. https://doi.org/10.1515/INTEG.2010.003.Google Scholar
Schlage-Puchta, J.-C., Regularity of a function related to the 2-adic logarithm. Bull. Belg. Math. Soc. Simon Stevin 18(2011), 375–377.Google Scholar
Shallit, J., A generalization of automatic sequences. Theoret. Comput. Sci. 61(1988), 1–16. https://doi.org/10.1016/0304-3975(88)90103-X.Google Scholar
Shu, Z. and Yao, J.-Y., Analytic functions over ℤp and p-regular sequences. C. R. Math. Acad. Sci. Paris 349(2011), 947–952. https://doi.org/10.1016/j.crma.2011.08.001.Google Scholar
Szilard, A., Yu, S., Zhang, K., and Shallit, J., Characterizing regular languages with polynomial densities. In: Mathematical foundations of computer science 1992 (Prague, 1992). Lecture Notes in Comput. Sci., 629, Springer, Berlin, 1992, pp. 494–503. https://doi.org/10.1007/3-540-55808-X_48.Google Scholar
van der Poorten, A. J. and Schlickewei, H. P., Additive relations in fields. J. Austral. Math. Soc. Ser. A 51(1991), 154–170.Google Scholar
Weyl, H., Über die Gleichverteilung von Zahlen mod. Eins. Math. Ann. 77(1916), 313–352. https://doi.org/10.1007/BF01475864.Google Scholar
Yasutomi, S.-I., On Sturmian sequences which are invariant under some substitutions. In: Number theory and its applications (Kyoto, 1997). Dev. Math., 2, Kluwer Acad. Publ., Dordrecht, 1999, pp. 347–373.Google Scholar