Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T16:06:04.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost Simplicial Polytopes: The Lower and Upper Bound Theorems

Part of: Polytopes and polyhedra

Published online by Cambridge University Press:  21 May 2019

Eran Nevo ,
Guillermo Pineda-Villavicencio ,
Julien Ugon  and
David Yost
Eran Nevo
Affiliation:
Institute of Mathematics, Hebrew University of Jerusalem, Israel Email: [email protected]
Guillermo Pineda-Villavicencio
Affiliation:
Centre for Informatics and Applied Optimisation, Federation University Australia Email: [email protected]
Julien Ugon
Affiliation:
School of Information Technology, Deakin University, Geelong, Australia Email: [email protected]
David Yost
Affiliation:
Centre for Informatics and Applied Optimisation, Federation University Australia Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study $n$-vertex 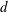$d$-dimensional polytopes with at most one nonsimplex facet with, say, 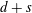$d+s$ vertices, called almost simplicial polytopes. We provide tight lower and upper bound theorems for these polytopes as functions of 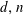$d,n$, and $s$, thus generalizing the classical Lower Bound Theorem by Barnette and the Upper Bound Theorem by McMullen, which treat the case where 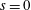$s=0$. We characterize the minimizers and provide examples of maximizers for any $d$. Our construction of maximizers is a generalization of cyclic polytopes, based on a suitable variation of the moment curve, and is of independent interest.

Keywords

polytopesimplicial polytopealmost simplicial polytopeLower Bound theoremUpper Bound theoremgraph rigidityh-vectorf-vector

MSC classification

Primary: 52B05: Combinatorial properties (number of faces, shortest paths, etc.)
Secondary: 52B12: Special polytopes (linear programming, centrally symmetric, etc.) 52B22: Shellability
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 2 , April 2020 , pp. 537 - 556
Copyright
© Canadian Mathematical Society 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research of E. Nevo was partially supported by Israel Science Foundation grants ISF-805/11 and ISF-1695/15. Research of J. Ugon was supported by ARC discovery project DP180100602.

References

Adiprasito, K. A. and Sanyal, R., Relative Stanley–Reisner theory and upper bound theorems for Minkowski sums. Publ. Math. Inst. Hautes Études Sci. 124(2016), 99–163. https://doi.org/10.1007/s10240-016-0083-7.Google Scholar
Asimow, L. and Roth, B., The rigidity of graphs. Trans. Amer. Math. Soc. 245(1978), 279–289. https://doi.org/10.2307/1998867.Google Scholar
Asimow, L. and Roth, B., The rigidity of graphs. II. J. Math. Anal. Appl. 68(1979), 171–190. https://doi.org/10.1016/0022-247X(79)90108-2.Google Scholar
Barnette, D. W., The minimum number of vertices of a simple polytope. Israel J. Math. 10(1971), 121–125. https://doi.org/10.1007/BF02771522.Google Scholar
Barnette, D. W., A proof of the lower bound conjecture for convex polytopes. Pacific J. Math. 46(1973), 349–354.Google Scholar
Billera, L. J. and Lee, C. W., A proof of the sufficiency of McMullen’s conditions for f-vectors of simplicial convex polytopes. J. Combin. Theory Ser. A 31(1981), 237–255. https://doi.org/10.1016/0097-3165(81)90058-3.Google Scholar
Billera, L. J. and Lee, C. W., The numbers of faces of polytope pairs and unbounded polyhedra. European J. Combin. 2(1981), no. 4, 307–322. https://doi.org/10.1016/S0195-6698(81)80037-6.Google Scholar
Braden, T., Remarks on the combinatorial intersection cohomology of fans. Pure Appl. Math. Q. 2(2006), no. 4, 1149–1186. https://doi.org/10.4310/PAMQ.2006.v2.n4.a10.Google Scholar
Braden, T. and MacPherson, R. D., Intersection homology of toric varieties and a conjecture of Kalai. Comment. Math. Helv. 74(1999), no. 3, 442–455. https://doi.org/10.1007/s000140050098.Google Scholar
Brøndsted, A., An introduction to convex polytopes. Graduate Texts in Mathematics, 90, Springer-Verlag, New York–Berlin, 1983.Google Scholar
Bruggesser, H. and Mani, P., Shellable decompositions of cells and spheres. Math. Scand. 29(1971), 197–205. https://doi.org/10.7146/math.scand.a-11045.Google Scholar
Goodman, J. E. and O’Rourke, J., eds. Handbook of discrete and computational geometry, Second ed., Discrete Mathematics and its Applications (Boca Raton), Chapman & Hall/CRC, Boca Raton, FL, 2004. https://doi.org/10.1201/9781420035315.Google Scholar
Grünbaum, B., Convex polytopes, Second ed., Graduate Texts in Mathematics, 221, Springer-Verlag, New York, 2003. https://doi.org/10.1007/978-1-4613-0019-9.Google Scholar
Kalai, G., Rigidity and the lower bound theorem. I. Invent. Math. 88(1987), no. 1, 125–151. https://doi.org/10.1007/BF01405094.Google Scholar
Kalai, G., Some aspects of the combinatorial theory of convex polytopes. In: Polytopes: abstract, convex and computational (Scarborough, ON, 1993). NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 440, Kluwer Acad. Publ., Dordrecht, 1994, pp. 205–229.Google Scholar
Karavelas, M. I. and Tzanaki, E., The maximum number of faces of the Minkowski sum of two convex polytopes. In: Proceedings of the Twenty-Third Annual ACM-SIAM Symposium on Discrete Algorithms. ACM, New York, 2012, pp. 11–22.Google Scholar
Karu, K., Hard Lefschetz theorem for nonrational polytopes. Invent. Math. 157(2004), 419–447. https://doi.org/10.1007/s00222-004-0358-3.Google Scholar
Kolins, S., f-vectors of triangulated balls. Discrete Comput. Geom. 46(2011), 427–446. https://doi.org/10.1007/s00454-010-9300-1.Google Scholar
McMullen, P., The maximum numbers of faces of a convex polytope. Mathematika 17(1970), 179–184. https://doi.org/10.1112/S0025579300002850.Google Scholar
McMullen, P., The numbers of faces of simplicial polytopes. Israel J. Math. 9(1971), 559–570. https://doi.org/10.1007/BF02771471.Google Scholar
McMullen, P. and Walkup, D. W., A generalized lower-bound conjecture for simplicial polytopes. Mathematika 18(1971), 264–273. https://doi.org/10.1112/S0025579300005520.Google Scholar
Murai, S. and Nevo, E., On the generalized lower bound conjecture for polytopes and spheres. Acta Math. 210(2013), no. 1, 185–202. https://doi.org/10.1007/s11511-013-0093-y.Google Scholar
Nevo, E. and Novinsky, E., A characterization of simplicial polytopes with g 2 = 1. J. Combin. Theory Ser. A 118(2011), 387–395. https://doi.org/10.1016/j.jcta.2009.12.011.Google Scholar
Stanley, R. P., The number of faces of a simplicial convex polytope. Adv. Math. 35(1980), 236–238. https://doi.org/10.1016/0001-8708(80)90050-X.Google Scholar
Stanley, R. P., Generalized H-vectors, intersection cohomology of toric varieties, and related results. In: Commutative algebra and combinatorics (Kyoto, 1985). Adv. Stud. Pure Math., 11, North-Holland, Amsterdam, 1987, pp. 187–213.Google Scholar
Whiteley, W., Infinitesimally rigid polyhedra. I. Statics of frameworks. Trans. Amer. Math. Soc. 285(1984), no. 2, 431–465. https://doi.org/10.2307/1999446.Google Scholar
Ziegler, G. M., Lectures on polytopes. Graduate Texts in Mathematics, 152, Springer-Verlag, New York, 1995. https://doi.org/10.1007/978-1-4613-8431-1.Google Scholar