¹ Of great value to the present writer were, in particular, Machlup, Fritz, International Trade and the National Income Multiplier (Philadelphia, 1943)Google Scholar, and Lange, Oscar, “The Theory of the Multiplier” (Econometrica1, vol. XI, 07-Oct., 1943, pp. 227–45).CrossRefGoogle Scholar

² Mathematically speaking, the home-induced export and import functions are fundamental relationships, whereas the foreign-induced export function is a derived relationship. In A, as X rises, Y rises, so

The same rise in exports lowers B's income, so

B's import function is then

Since Y_A and M_B are both functions of X_A ,

as long as dX_A ≠ 0, which is the case here.

³ I am indebted to Professor G. A. Elliott for the rewriting of this sentence.

⁴ As follows: the equilibrium condition, expressed in terms of induced changes, is that ΔZ_B = ΔL_B . Hence,

giving us

Now A's final increase in income is composed as follows:

Then,

Substituting (a) in (b), we have

which gives us

If I′ and X′ are zero in both systems, this is the same as Dr. Machlup's “investment multiplier” (International Trade and the National Income Multiplier, pp. 126-8).

⁵ As follows: A's change in income consists of the initial increment in the trade balance plus the home-induced changes:

so that

Since ΔY_B = _Bk_B ( − ΔZ_B ), substitution of (6) in (c) gives

from which we derive

⁶ International Trade and the National Income Multiplier, p. 78. The inter-expenditure multiplier may be derived directly. The equilibrium condition in terms of induced changes is that ΔZ_A = − ΔZ_B . That is,

A's final increase in income is made up as follows:

Substituting (d) in (e) we obtain

given us

so that

⁷ It is possible, by means of a simple device, to illustrate the dynamics of income changes in the above diagram; lack of space, however, does not allow us to include a discussion of the dynamics of the bi-system multiplier in this paper. It suffices here to point out that stability requires that the slope of L ₂ be greater than Z's slope minus two, that is,

If L ₂ is steeper than this, income will oscillate explosively, and the automatic mechanisms designed to steepen L ₂ will defeat their purpose.

⁸ For a detailed discussion of the maintenance of economic stability by means of automatic devices, see Milton Friedman, “A Monetary and Fiscal Framework for Economic Stability” ( American Economic Review, vol. XXXVIII, 06, 1948, pp. 245–64Google Scholar). See also the following: Lange, Oscar, Price Flexibility and Employment (Bloomington, Indiana, 1944)Google Scholar; Patinkin, Don, “Price Flexibility and Full Employment” (American Economic Review, vol. XXXVIII, 09, 1948, pp. 543–64Google Scholar; Pigou, A. C., “The Classical Stationary State” (Economic Journal, vol. LIII, 12, 1943, pp. 343–51CrossRefGoogle Scholar).

⁹ The precise meaning in this case of the excess saving and trade balance functions, as well as a fuller analysis of the application of the bi-system multiplier to the problem of income distribution between capitalists and workers, is dealt with in a chapter entitled “The Class Struggle Multiplier” in my unpublished thesis, Introduction to the Generalized Theory of Multi-System Macroeconomics, Redpath Library, McGill University, pp. 41-8.

¹⁰ If L ₃ is too steep (see note 7) income may be oscillatory; that is, a rise in wages will bring about a rise in profits, followed by a further rise in wages, etc. Thus a temporary rise in profits is theoretically possible.

¹¹ A retaliatory increase in prices, for instance, would be shown by a downward shift of B's excess savings function. Further induced shifts of the excess saving and trade balance functions may be analysed along the lines of the analysis presented in Dr. Lange's Price Flexibility and Employment.

¹² Dr. Machlup's multipliers are clearly all special cases of (11). So are Dr. Lange's. The latter's “internal spending multiplier” (“Theory of the Multiplier,” p. 233) is written

where E ₁ is autonomous internal expenditure, E ₁′ and E ₂′ are the marginal propensities to spend internally and externally, and R′ is the other system's marginal propensity to spend back. (f) is equivalent to (6), where

Dr. Lange's “total spending multiplier” (pp. 234-5) is written

(h) is a special case of (11) in which α = E ₁′ and β = E ₂′.

¹³ For a fuller treatment of the regional multiplier, cf. Chipman, , “Multi-System Macroeconomics,” pp. 49–53.Google Scholar

¹⁴ (15) is equivalent to the expression 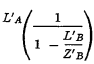in (6), and is equal to the slope of L ₃ in Figure 5A.