No CrossRef data available.
Article contents
Economic Growth and International Trade in a Simple Dynamic Leontief Model*
Published online by Cambridge University Press: 07 November 2014
Extract
Traditional Keynesian trade multipliers ignore intermediate goods. Professors Harrod and Johnson have considered them in a limited sense; both used a one-sector model. The objects of this paper are: to consider the effect of intermediate goods on the trade multiplier by use of a matrix trade multiplier; to consider their effect on the rate of growth of both exports and outputs of commodities; and to discuss the stability conditions of a balanced growth rate in a simple dynamic Leontief model.
Harrod took intermediate goods into account only as a deduction from exports or investments when he considered the multiplier process. Johnson considered them more explicitly. In his model, an economy uses a primary factor of production, say labour, and foreign-made intermediate goods to produce consumption goods. However, the economy does not use home-produced intermediate goods, and all home-produced goods are consumption goods (so that the economy exports only consumption goods). In a more realistic model, the autonomous increment of demand for investments or exports would create two kinds of multiplier processes: one through the increment of demand for home-produced consumption goods, the other through the demand for home-produced intermediate goods. Each industry uses a primary factor of production and both home-made and foreign-made intermediate goods. Consumers demand both domestic and foreign consumption goods.
L’integration de la croissance economique et du commerce international a un modele dynamique simple leontief
Le modèle que nous avons élaboré est une synthèse des modèles de Leontief et de Keynes en ce que: (1) les coefficients du modèle Leontief englobent des termes reliant non seulement les produits intermédiaires domestiques et le travail mais aussi des produits intermédiaires importés; et (2) une fonction de consommation est employée dans le modèle Leontief.
L'équation fondamentale de notre modèle est obtenue en utilisant une matrice de multiplicateurs de commerce. Le processus de multiplication peut être décomposé en deux étapes: d'abord les effets de répercussion directs; puis les effets de répercussion indirects. A cette occasion, nous montrons comment les multiplicateurs de commerce de Keynes et de H. G. Johnson sont des cas particuliers de ceux que nous avons élaborés.
Dans la partie de ce travail où le modèle est dynamisé, nous avons établi à la façon coutumière une relation fonctionnelle entre l'investissement et ses répercussions sur les produits. Nous avons cependant poussé plus loin notre analyse en formulant une équation dynamique fondamentale. Là encore, nous montrons que le modèle de Johnson est un cas particulier de notre modèle.
Trois conclusions semblent se dégager:
1. Si l'investissement de chaque industrie est une forte proportion de la production des autres industries dans la matrice des coefficients de capital, le système économique est stable, l'économie tend vers un taux de croissance d'équilibre et vice versa.
2. L'accroissement des produits dans les deux industries sans changement dans les exportations n'accroît pas nécessairement les taux de croissance des deux industries.
3. En fait, lorsque les exportations s'accroissent, le revenu national s'accroît mais le taux de croissance de l'économie peut décroître.
- Type
- Research Article
- Information
- Canadian Journal of Economics and Political Science/Revue canadienne de economiques et science politique , Volume 32 , Issue 1 , February 1966 , pp. 55 - 65
- Copyright
- Copyright © Canadian Political Science Association 1966
Footnotes
This article is part of my PhD thesis submitted to the University of Rochester in June 1965. I have benefited from discussions with Professor Ronald W. Jones. I am also indebted to the referee of this article for useful comments.
References
1 Harrod, R. F., The Trade Cycle (Oxford, 1936).Google Scholar
2 Johnson, H. G., “Equilibrium Growth in an International Economy,” this Journal, XIX, 4 (11 1953), 478–500 Google Scholar, reprinted in International Trade and Economic Growth (London, 1958), chap. v.Google Scholar
3 The Trade Cycle, 153–4.
4 Solow, R. M. and Samuelson, P. A., “Balanced Growth under Constant Returns to Scale,” Econometrica, 21 (07 1953), 412–24.CrossRefGoogle Scholar
5
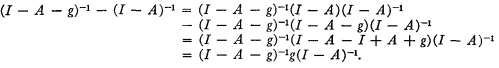
6 Substitute the relation K ij(t) = kijXj (t) for equation (17) to obtain K(t) = k(I − A − g)−1 {II + E} = β{II + E] = β{K(t + 1) − K(t) + E(t + 1)} where β is k(I − A − g)−1. Rearrange each term to obtain (I + β)K(t) = β[K(t + 1) + E(t + 1)]. This corresponds to Dorfman, R., Samuelson, P.A., and Solow's, R. M. result in Linear Programming and Economic Analysis (New York, 1958), 291–2.Google Scholar
7 These conditions correspond to the stability condition of the neo-classical model of economic growth. That is, in the case of the neo-classical model, if the investment good is labour-intensive and the consumption good is capital-intensive, then the economy is stable. See, for instance, Jones, R. W., “The Structure of Simple General Equilibrium Models,” Journal of Political Economy (12 1965).CrossRefGoogle Scholar


