Introduction
Phenology considers the effect of seasonal changes in environmental conditions on the timing and progression of life stages and associated eco-physiological events in an organism's life history. For poikilotherms such as insects, the time-scale of their phenology is expressed most appropriately on a physiological rather than a calendar time-scale to account for the dominating effects of temperature on rates of growth and development (Gilbert and Raworth Reference Gilbert and Raworth1996) and stabilisation of life cycles (Powell and Logan Reference Powell and Logan2005). Temperature-driven phenology models transcribe events from a calendar to a species-specific physiological time-scale and allow insight into the pervasive influence of weather and climate on processes affecting insect populations. These models are incisive tools in ecology that improve our understanding of birth and survival rates and trophic interactions that vary over time in seasonally heterogeneous environments (Both et al. Reference Both, van Asch, Bijlsma, van den Burg and Visser2009), and in evolution by revealing mechanisms of genetic isolation (Lumley and Sperling Reference Lumley and Sperling2011). A critical application of these models is predicting the influence of novel weather patterns on the behaviour of pest populations, whether this influence applies to alien species spreading in new environments (e.g. Régnière et al. Reference Régnière, Nealis and Porter2009) or to indigenous species exposed to a changing climate (e.g. Thomson and Benton Reference Thomson and Benton2007; Bentz et al. Reference Bentz, Régnière, Fettig, Hansen, Hayes and Hicke2010; Régnière et al. Reference Régnière, St-Amant and Duval2012b).
Process models have several advantages over correlative models in ecology, including their greater generality and relevance over a range of conditions (Korzukhin et al. Reference Korzukhin, Ter-Mikaelian and Wagner1996). Process models are preferred for the analysis of phenology because of their mechanistic, functional link to known eco-physiological responses (Volney and Fleming Reference Volney and Fleming2007) combined with advances in the application of robust experimental designs and data analysis (Régnière et al. Reference Régnière, Powell, Bentz and Nealis2012a). Increased computing power has enabled further realism in modelling emergent biological phenomena such as phenology via individual-based models that simulate life history processes of individuals with intrinsic variability in development, survival, and reproductive rates within populations (Régnière and Logan Reference Régnière and Logan2003; Grimm and Railsback Reference Grimm and Railsback2005; Régnière et al. Reference Régnière, Powell, Bentz and Nealis2012a).
Régnière (Reference Régnière1982, Reference Régnière1987, Reference Régnière1990) developed process-oriented phenology models for the spruce budworm, Choristoneura fumiferana (Clemens) (Lepidoptera: Tortricidae), to integrate seasonal development and stage-specific mortality and natality. These models have practical application in population ecology (Régnière and You Reference Régnière and You1990), pest management (Cooke and Régnière Reference Cooke and Régnière1996), and the exploration of the potential effects of climate change on population behaviour (Régnière et al. Reference Régnière, St-Amant and Duval2012b). This paper provides a phenology model for western spruce budworm, C. occidentalis Freeman, based on measurements of individual rates of development and survival of all immature stages, as well as adult longevity and rate of oviposition, under controlled temperatures. The model is calibrated and validated with observations from field populations in several locations and years in British Columbia (BC), Canada, to ensure its ability to produce realistic simulations of actual events over a range of natural conditions. It reproduces observed phenology, has sufficient detail to examine stage-specific ecological relationships between the insect and its environment throughout its life history, and permits simulation of multi-generation, seasonal behaviour of populations. It can be used to determine the impact of climate change on the insect's seasonality.
Materials and methods
Life history of western spruce budworm
The western spruce budworm is a native defoliator of conifers in western North America. The principal host in BC is Douglas-fir, Pseudotsuga menziesii (Mirbel) Franco (Pinaceae) but spruce (Picea Dietrich, Pinaceae) and especially true fir (Abies Miller, Pinaceae) are also susceptible (Furniss and Carolin Reference Furniss and Carolin1977). The insect is univoltine with obligate diapause under field conditions. Moths are active in the interior of BC from mid-July to September, depending on elevation and year. Eggs are laid in masses on host needles and hatch within two weeks. Neonate larvae (L1) do not feed but disperse to protected niches throughout the tree where they establish hibernaculae, moult to a second instar, enter diapause and overwinter (L2o). Diapause development is complete by February and budworms enter a dormant stage, ready to resume development when temperatures become sufficiently warm. Time of emergence of these larvae in the spring varies from late-April to June depending on weather (Nealis and Nault Reference Nealis and Nault2005). Feeding budworms complete a total of six instars (L2−6) and pupate in late June to mid-August.
Historical evidence suggests an increase in the extent of outbreaks of the western spruce budworm in the past century in the United States of America, associated with apparent changes in forest structure but also weather (Swetnam and Lynch Reference Swetnam and Lynch1993). Similar increases in the extent of outbreaks have been observed in BC, particularly since 2000 when outbreaks were observed further north and at higher elevations than previously recorded (Nealis et al. Reference Nealis, Noseworthy, Turnquist and Waring2009), suggesting a link to changes in critical population processes under the influence of weather patterns (Thomson and Benton Reference Thomson and Benton2007).
Development and oviposition in the laboratory
Western spruce budworm stock was derived from larvae collected from Douglas-fir at several locations in the interior of BC (Nealis et al. Reference Nealis, Noseworthy, Turnquist and Waring2009) and reared individually on artificial diet (McMorran Reference McMorran1965) at 20 °C and light:dark cycle of 18 hours:6 hours. Surviving moths of this wild generation were used to measure temperature-dependent adult longevity, fecundity, and rates of oviposition. Their first-generation progeny were the eggs, larvae, and pupae used for measurement of stage-specific rates of development.
Longevity of female moths and rates of oviposition were measured by placing a freshly emerged female moth and two male moths to mate in a 1-L glass jar containing fresh foliage of Douglas-fir and covered with wire mesh. Moths were left for no more than 16 hours at 20 °C and then the cage units were assigned to one of five constant temperatures (nominal 12 °C, 16 °C, 20 °C, 24 °C, and 28 °C) and light:dark cycle of 18 hours:6 hours. Moths and foliage were checked daily and all egg masses removed. The number of egg masses, the number of eggs per mass, and the date of death of the female moth were recorded. Female fertility was defined by at least one egg hatch. Infertile females were excluded from analysis because unmated females lay few eggs.
The developmental response of western spruce budworm eggs to temperature was described by Régnière et al. (Reference Régnière, Powell, Bentz and Nealis2012a) using eggs from this experimental setup. Remaining egg masses were used to produce overwintering larvae. A random subset of these hibernating, second-instar larvae (L2o) was taken in mid-August 2008, to overwinter inside protective wire cages suspended from a mid-crown branch in trees at field sites near Merritt, BC. Unpublished studies of overwintering western spruce budworm by V.G.N. indicate that diapause development in this species is similar to that described for spruce budworm by Régnière (Reference Régnière1990) with diapause termination in mid-winter followed by increasing sensitivity to warming temperatures that tends to synchronise the emergence time of each generation. Accordingly, western spruce budworm L2o were retrieved from their field locations in late February 2009 when diapause had terminated but field temperatures were sufficiently low that negligible post-diapause development would have occurred and assigned to one of five constant temperatures (12 °C, 16 °C, 20 °C, 24 °C, and 28 °C). They were checked daily to observe their post-diapause rate of emergence.
The remaining L2o were overwintered for six months at 2 °C in the laboratory. These budworms were then brought to 20 °C, allowed to emerge, and placed individually in glass vials containing artificial diet inverted over clean, white sand in plastic racks and placed at one of the five constant temperatures. Constant 12 °C is too cold for the behavioural requirements of budworm feeding so rates of development at this low temperature treatment used a variation of the method of temperature-transfer described by Régnière et al. (Reference Régnière, Powell, Bentz and Nealis2012a). Larvae were first placed at 20 °C so they could establish a feeding site, then placed at 12 °C for at least seven days, and finally returned to 20 °C to allow moulting and completion of the instar.
Developing spruce budworm larvae were observed daily and the date of ecdysis to each subsequent instar, indicated by the presence of a cast-off head capsule, was recorded. Head capsules were removed and a subset measured to enable identification of the stages of insects collected in the field (see below). The date of pupation was recorded. Pupae were left undisturbed for 24 hours to harden and then removed from the glass vial, their sex determined, and placed individually in a dry plastic creamer cup with a cardboard lid. Pupae were re-assigned randomly to one of the five experimental temperatures and the time to adult emergence was recorded.
Data analysis
To estimate parameters of developmental response curves of each life stage, we used a maximum-likelihood approach that fits functions and estimates variability among individuals from the observed development times of individuals, tij, where i is the individual and j is a constant temperature or a temperature-transfer treatment (Régnière et al. Reference Régnière, Powell, Bentz and Nealis2012a). The method expresses individual variation as relative development rates, δij, and estimates a lack-of-fit variation, ρj, between the theoretical thermal response, τ(T, A) and the expected mean development time:
$${{{t}_{ij}}\, = \,{{{\rm{\rdelta }}}_{ij}}{{{\rm{\rrho }}}_j}{\rm{\rtau }}(T,{\bf {{A}}})\eqno[1]$$
where A is the maximum-likelihood set of parameter values of the thermal response function across a range of temperatures, T. Individual variation was log normally distributed with variance 
$$${\rm{\rsigma }}_{{\rm{\rdelta }}}^{{\rm{2}}} $$$
and mean 1 and lack of fit was distributed normally with variance 
$$${\rm{\sigma }}_{{\rm{\rrho }}}^{{\rm{2}}} $$$
and mean 1.
The developmental rates, r, of stages from L2o to pupa and eggs were described by the enzyme thermodynamics model of Sharpe and DeMichele (Reference Sharpe and DeMichele1977) modified by Schoolfield et al. (Reference Schoolfield, Sharpe and Magnusun1981):
$${r({{T}_K},\ {\bf {{A}}})\, = \cr \,\frac{{{{{\rm{\rrho }}}_{{\rm{25}}}}\frac{{{{T}_K}}}{{{\rm{298}}}}\exp \left[ {\frac{{{{H}_A}}}{R}\left( {\frac{{\rm{1}}}{{{\rm{298}}}}\,{\rm{ - }}\,\frac{{\rm{1}}}{{{{T}_K}}}} \right)} \right]}}{{{\rm{1}}\, + \,\exp \left[ {\frac{{{{H}_L}}}{R}\left( {\frac{{\rm{1}}}{{{{T}_L}}}\,{\rm{ - }}\,\frac{{\rm{1}}}{{{{T}_K}}}} \right)} \right]\, + \,\exp \left[ {\frac{{{{H}_H}}}{R}\left( {\frac{{\rm{1}}}{{{{T}_H}}}\,{\rm{ - }}\,\frac{{\rm{1}}}{{{{T}_K}}}} \right)} \right]}}\eqno[2]$$
where TK is temperature (°K), R = 1.987 is the universal gas constant, and 
$$${\bf {{A}}}\, = \,\left\{ {{{{\rm{\rrho }}}_{{\rm{25}}}},{{H}_A},{{H}_L}, <$> <$> {{T}_L},{{H}_H},{{T}_H}} \right\}$$$
. The relationship between temperature and adult longevity (days) was modeled with a third degree polynomial:
$${{\rtau (T,}}{\bf \ {{A}}}{\rm{)}}\,{\rm{ = }}\,a\, + \,bT\, + \,c{{T}^{\rm{2}}} \, + \,d{{T}^{\rm{3}}} \eqno[3]$$
where T is temperature (°C) and A = {a,b,c,d}. Values of 
$$${\rm{\rsigma }}_{{\rm{\rdelta }}}^{{\rm{2}}} $$$
and 
$$${\rm{\rsigma }}_{{\rm{\rrho }}}^{{\rm{2}}} $$$
in equation [1] and of parameter set A in equations [2] or [3] were estimated simultaneously by maximum likelihood (see Régnière et al. Reference Régnière, Powell, Bentz and Nealis2012a).
The data for temperature-dependent rate of oviposition were analysed by the method suggested by Régnière et al. (Reference Régnière, Powell, Bentz and Nealis2012a), because they exhibited a typical diminishing-return pattern over time for all temperatures:
$$\frac{{dF}}{{dt}}\, = \,{\rm{ - }}{{O}_t}\, = \,{\rm{ - }}\rkappa (T,{\bf {{B}}}){{F}_t}\eqno[4]$$
where Ot, the number of eggs laid on day t, is the product of a female's remaining fecundity Ft and 
$$$\rkappa $$$
(T, B), the probability of an egg being laid at time t. T is temperature (°C) and B is a vector of parameters. Solving [4] at constant temperature T yields 
$$${{F}_t}\, = \,{{{\rm{\reta }}}_{ij}}{{e}^{{\rm{ - }}\rkappa {(T,\,\bf B)}(t\,{\rm{ - }}\,{{t}_0})}} $$$
where ηij is a female's total (initial) fecundity, a lognormally distributed random variable with mean = 1 and variance 
$$${\rm{\rsigma }}_{{\rm{\reta }}}^{{\rm{2}}} $$$
. In our dataset, the pre-oviposition period, t 0, is approximately one day (two days at temperature ≤12 °C). Moths may oviposit several or no egg masses on any given day so the interval between ovipositions, Δt, may be more than one day. Régnière et al. (Reference Régnière, Powell, Bentz and Nealis2012a) show that the number of eggs expected during these intervals is:
$$no{{{O}_{ij}}\, = \,{{{\rm{\reta }}}_{ij}}\left[ {{{e}^{{\rm{ - }}\rkappa ({{T}_j},\,{\bf B})(t\,{\rm{ - }}\,\rDelta t\,{\rm{ - }}\,{{t}_0})}} {\rm{ - }}{{e}^{{\rm{ - }}\rkappa ({{T}_j},\,{\bf {B}})(t\,{\rm{ - }}\,{{t}_0})}} } \right] \cr {\rm{for}}\,t\geq {{t}_0}\, + \,\rDelta t [5]$$
Several forms of function 
$$$\rkappa $$$
(T, B) expressing the relationship between temperature and the proportion of remaining fecundity laid per interval were tested. This relationship increased non-linearly with temperature, and was inversely proportional to remaining fecundity. The best model obtained was:
$${\rm{\kappa }}(T,{\bf {{B}}})\, = \,{{{\rm{\rbeta }}}_{\rm{1}}}\, + \,{{{\rm{\rbeta }}}_{\rm{2}}}T\, + \,{{{\rm{\rbeta }}}_{\rm{3}}}\sqrt T \, + \,{{{\rm{\rbeta }}}_{\rm{4}}}\,/\,{{F}_t}\eqno[6]$$
The values of 
$$${\rm{\rsigma }}_{{\rm{\eta }}}^{{\rm{2}}} $$$
and of parameter set 
$$${\bf {{B}}}\, = \,\{ {{{\rm{\rbeta }}}_{\rm{1}}}{\rm{,}}{{{\rm{\rbeta }}}_{\rm{2}}}{\rm{,}}{{{\rm{\rbeta }}}_{\rm{3}}}{\rm{,}}{{{\rm{\rbeta }}}_{\rm{4}}}\} $$$
were estimated by maximum likelihood (see Régnière et al. Reference Régnière, Powell, Bentz and Nealis2012a).
Seasonality model
The seasonality model uses daily minimum and maximum air temperatures as input and calculates development and reproduction at a four-hour time step. Temperature is interpolated between successive daily minimum and maximum readings by the half-sine method of Allen (Reference Allen1976). The output is the daily number of individuals alive in each of eight life stages: overwintering L2o, feeding L2, L3; L4; L5; L6 (includes supernumerary instar when it occurs), pupa, adult, and egg. We do not explicitly model L1 development, but assume that neonates enter diapause very soon after hatch and become L2o. Calculation of spring development begins 1 March when all live, overwintering individuals of each generation have completed diapause and are responsive to warmer temperatures. Each individual, created as an overwintering L2o in the initial generation and as an egg in subsequent generations, is assigned randomly a relative development rate for each life stage, a gender (1:1 sex ratio), and a potential fecundity, η (females). This model is stochastic, so output varies between runs.
Field observations
Direct observations of the phenology of budworm populations in the field were made at several locations, years and times during the season (Nealis and Nault Reference Nealis and Nault2005; Nealis et al. Reference Nealis, Noseworthy, Turnquist and Waring2009). The timing of L2 spring emergence and dispersal was estimated using sticky traps in some locations (Nealis and Régnière Reference Nealis and Régnière2009). This same method was used to estimate the time of L1 egg hatch later in the summer as this stage also disperses and can be monitored similarly. The phenology of feeding larvae and pupae was measured by sampling branches periodically from several sites during the season, removing the insects and recording the distribution of life stages by measurement of head capsules on all insects. To test goodness of fit, and for graphical presentation of model output, the age distribution for each collection date at each site was summarised as an average instar.
Comparison of model output with field data
The phenology model was run in BioSIM (Régnière et al. Reference Régnière, St-Amant and Béchard2013) using maximum and minimum temperatures from the nearest eight Environment Canada weather stations, weighted according to the inverse of distance from the target site and similarity in elevation or, in some cases, using on-site temperature records. The accuracy of model predictions of L2 emergence was determined by testing the difference (t-test) between dates at which the predicted proportion emerged corresponded to observations. Observations of L1 capture on sticky traps were compared graphically to predicted hatch (all in 2008).
In spruce budworm, L2 develop more slowly on artificial diet than on host foliage (Régnière et al. Reference Régnière, St-Amant and Duval2012b). Under our experimental conditions, newly emerged western spruce budworm often wandered for a day or more before feeding on artificial diet inside the glass tube. To compensate for this influence of diet, an L2 rate-parameter (ρ25) adjustment multiplier was estimated using a simulated annealing algorithm to maximize the likelihood of observed life-stage frequencies in foliage samples. The likelihood was calculated from observed numbers in each of the eight life stages in a given sample j (
$$${{{\bf {{X}}}}_j}\, = \,\left\{ {{{x}_{{\rm{1}}j}},{{x}_{{\rm{2}}j}}, \ldots, {{x}_{{\rm{8}}j}}} \right\}$$$
, with 
$$${{n}_j}\, = \,\mathop{\sum}\nolimits_{i\,{\rm{ = }}\,{\rm{1}}}^{\rm{8}} {{{x}_i}_{j} } $$$
, and the expected relative stage frequencies pij output by the model, where 
$$$\mathop{\sum}\nolimits_{i\,{\rm{ = }}\,{\rm{1}}}^{\rm{8}} {{{p}_{ij}}\,{\rm{ = }}\,{\rm{1}}} $$$
, with the multinomial probability distribution:
$$L\, = \,{\rm{ - }}\mathop{\sum}\limits_j {\log } \left[ {\frac{{{{n}_j}!}}{{{{x}_{1j}}! \ldots {{x}_{8j}}!}}p_{{1j}}^{{{{x}_{ij}}}} \ldots p_{{8j}}^{{{{x}_{ij}}}} } \right]\eqno[7]$$
where j refers to a foliage sample. The foliage sample dataset was divided in two near-equal halves (by site-year), using 56 site-years for parameter estimation (141 samples) and the remaining 58 site-years for model validation (142 samples).
Independent field data were provided by Lumley and Sperling (Reference Lumley and Sperling2011) who trapped moths of C. occidentalis and C. fumiferana at several locations in Cypress Hills, an isolated forest area in the prairies of southwestern Canada, throughout the flight season of 2008. We used our phenology model for C. occidentalis and the one described by Régnière et al. (Reference Régnière, St-Amant and Duval2012b) for C. fumiferana to predict flight phenology of these closely related species in the same area in the same year and so examine the robustness of these models outside the geographic regions in which they were developed.
Phenology at the landscape level
We used BioSIM 10 (Régnière et al. Reference Régnière, St-Amant and Béchard2013) to generate maps of the expected date at which the relative frequency of L4C. occidentalis larvae reaches it maximum (peak L4) in southern BC based on 1981–2010 normals. This phenological event is significant to forest pest managers as it indicates the time when most budworms have emerged and established feeding sites in current-year foliage and therefore the beginning of the period of susceptibility to pesticides.
Change in phenology between 1951 and 2012
Once again using BioSIM 10, and historical daily weather data from the Environment Canada database, we ran the phenology model for three locations in BC: Alexis Creek (52.116°N, −123.39°E, 880 m), Lower Veasy Creek (50.909°N, −121.562°E, 1245 m) and Clapperton (50.182°N, 120.669°E, 750 m), for the years 1951–2012. Because the model is stochastic, each run was replicated 10 times and results were averaged over replicates. To check for a trend over time, the date of peak L4 was regressed against year, using location as a factor.
Results
Developmental responses to temperature and individual variability
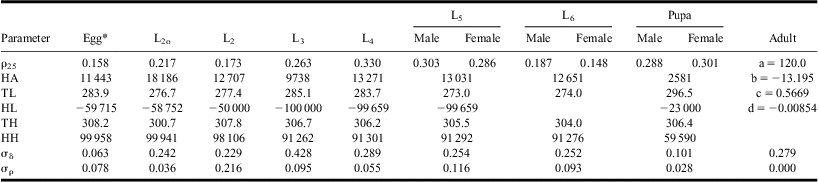
Equations [1] and [2] were fitted simultaneously to individual development times of all stages, from L2o to pupa, and equations [1] and [3] were used to describe the relationship between temperature and adult longevity (Fig. 1; Table 1). Although data from temperatures < 12 °C or >30 °C were not available, the algorithm produced realistic estimates of upper and lower threshold temperatures within the bounds (HL ≥ 273, HH ≤ 308°K), except in L5 for which the estimate converged to HL = 273°K. Adult longevity at 12 °C averaged 30 days and the value predicted by equation [3] was limited to this maximum longevity for temperatures ≤12 °C. Equation [3] also predicted adult longevity <0 at temperatures >32 °C. In the model, adults die of old age in one time step at such temperatures.
Fig. 1 Responses to temperature in eight successive life stages, from L2o to adult longevity. Left column: development times; centre column: development rates. Solid lines: equation [2]. Dotted lines: ±3σδ. Right column: corresponding rate distributions (lines are the lognormal distribution with mean 1 and variance 
$$${\rm{\rsigma }}_{{\rm{\rdelta }}}^{{\rm{2}}} $$$
). Data at 12 °C from temperature transfer treatments (▴), except L2o and adults. Where colour is used: black for males, red for females.
Table 1 Parameter values of mean developmental responses to temperature (L2o to pupa: equation [2]; adult: equation [3]).
*From table 2 in Régnière et al. (Reference Régnière, Powell, Bentz and Nealis2012a).
Individual variability in development, as expressed by the lognormal distribution parameter, 
$$${{{\rm{\rsigma }}}_{\rm{\rdelta }}}$$$
, ranged between 0.184 in pupae and 0.428 in L3, reflecting well the distribution of development times and rates in all stages (Fig. 1).
There were weak correlations between successive life stages (L2 to pupa) in an individual's deviation from the mean population development time, 
$$${{\rdelta }_i}$$$
, although some correlations were significantly different from 0 (r 2−3 = 0.151, P < 0.001; r 3−4 = 0.1, P = 0.007; r 5−6 = −0.094, P = 0.018). Therefore, random numbers were used to generate stage-specific, relative development rates in individuals for the simulations.
The simplest form of the oviposition model, equation [6], using only parameter β1, (i.e. oviposition is independent of temperature) produced a reasonable fit to the average daily oviposition data (R 2 = 0.79) but adding the temperature dependence parameter β2 increased the fit significantly (R 2 = 0.87). Adding parameters β3 and β4 improved the fit only slightly (R 2 = 0.88) but increased the maximum likelihood significantly as judged by Akaike's corrected information criterion (AICc) (Fig. 2; Table 2). Thus, the full four-parameter model was retained.
Fig. 2 Observed (• ± SEM) and simulated (equation [5]) oviposition rate as a function of time at (A) 12 °C; (B) 16 °C; (C) 20 °C; (D) 24 °C; and (E) 28 °C; (F) relationship between oviposition thermal response and temperature (equation [6] with Ft = 250 eggs).
Table 2 Parameters for oviposition model (equation [6]) with increasing complexity from constant proportion to full model.
Notes: R 2 values calculated by correlating average observed daily oviposition rates to predicted values. While the gain in AIC with increasing complexity is quite significant, the gain in R 2 is not as pronounced.
No significant effect of temperature on total fecundity was detected (F 4,54 = 1.76, P = 0.149). Average lifetime fecundity was high: η = 244.1±83.4 (SD; n = 67) and normally distributed (Anderson-Darling statistic = 0.196, P = 0.886) so fecundities among individual females in the simulated population were random draws from this distribution.
Comparison of model output with field data
The model predicted emergence of post-diapause budworms in the spring 3.6 days earlier than observed; a significant and consistent bias (mean pairwise difference: 3.7 days, t 245 = 8.8, P < 0.001; slope of regression of observed on simulated emergence dates: 0.93 ± 0.038, not significantly different from 1, t 244 = −1.85, P = 0.066; R 2 = 0.71). This bias is the result of the method of estimating L2 spring emergence time by observing dispersing budworms on sticky traps. Actual emergence necessarily precedes dispersal of larvae and capture on traps. Furthermore, L2 disperse throughout the stage as they alternate between needle mining and foraging for suitable current-year buds (Nealis and Nault Reference Nealis and Nault2005). Given this bias, the overall time trends of simulated L2 emergence were often in advance of the observed cumulative L2 capture on sticky traps in the 16 plot-years with sufficient data for graphical comparison (Fig. 3; >40 larvae/m2, >4 observations, first observation representing <5% of total catch). Nonetheless the variability of predicted L2 emergence, caused entirely by the lognormal distribution of individual development rates, corresponds well with the distribution of L2 dispersal observed on sticky traps so that the period of emergence, if not the actual dates, is well mimicked by the model.
Fig. 3 Observed cumulative capture of L2 on sticky traps (•) and simulated cumulative emergence of L2 from overwintering (lines) in 16 plot years with total catch >40 larvae/m2 and first observation representing <5% of total catch.
The reluctance of emerging L2 to feed on artificial diet prolonged artificially the duration of this instar in our experiments. As a result, the model had a significant late bias of nearly half an instar (mean pairwise difference = −0.48, t 283 = 15.7, P < 0.001). The adjustment factor of development rates of feeding L2 obtained by simulated annealing using a subset of half our foliage samples was 2.62 × ρ25 (L2). This adjustment removed any significant bias between predicted and observed average instar (mean pairwise difference = 0.16, t 283 = 3.3, P = 0.185). The regression between observed and predicted average instar among the validation subset of foliage samples had a slope of 0.977, not significantly different from 1 (t 140 = −0.9, P = 0.37; R 2 = 0.91).
Model output for all stages, once adjusted for faster L2 development rates, compared well with observed life stage frequencies in foliage samples, both in terms of timing and spread of the distributions (Fig. 4). Note the “missing” observation of peak L5 in Fig. 4B resulting from insufficient sampling frequency to track actual phenology of this relatively brief life stage. Simulated and observed time trends in average instar among the 20 plot years with sufficient data (n ≥ 4) match closely (Fig. 5).
Fig. 4 Comparison of simulated and observed life stage frequencies on branch samples at Mabel Creek, British Columbia, Canada, in 2008.
Fig. 5 Observed (•) and simulated (lines) average instar in 20 plot years with more than three observations.
The final comparison with field observations comes from captures of dispersing L1 on sticky traps compared with the timing of egg hatch predicted by the model (Fig. 6).
Fig. 6 Comparison of observed cumulative catch of L1 on sticky traps (•) and simulated cumulative egg hatch (solid line), averaged over six locations in British Columbia, Canada from which observations were available (2008). First observation: traps set up, 0 dispersal is presumed, but may have been higher.
Application of separate phenology models for western and eastern spruce budworms to the observations of moth captures of both species in the Cypress Hills by Lumley and Sperling (Reference Lumley and Sperling2011) demonstrated the robust nature of these two process models and provided further insight into eco-physiological distinctions between these closely related species. Flight of C. fumiferana was observed earlier in the season than that of C. occidentalis (Fig. 7A). Interpretation of this apparent difference between the phenologies of these species, however, was confounded by sample locations; more C. fumiferana were found in the northeast section of the sampled area at lower elevations and more C. occidentalis were found in the southwest section at higher elevations (Lumley and Sperling Reference Lumley and Sperling2011). Our phenology models predict that although the phenology of those two species is affected similarly by elevation, the flight of C. occidentalis occurs later than that of C. fumiferana at all elevations (Fig. 7B), due to their different thermal responses.
Fig. 7 (A) Temporal distribution of moth captures of Choristoneura fumiferana and C. occidentalis in pheromone traps in Cypress Hills, Alberta, Canada from Lumley and Sperling (Reference Lumley and Sperling2011) and (B) ordinal date of simulated peak flight of both species along elevation gradient.
Phenology at the landscape level
The phenology of western spruce budworm varies considerably as a function of topography and regional climates in BC. This is important from an ecological as well as a pest management perspective. The L4, for example, is a potential target life stage for pesticide applications. The model can be used to determine the date of occurrence of this life stage over variable terrain and weather (Fig. 8). The predicted timing of peak L4 over the southern half of BC ranges from the first week of May to well into July. Nearly as much variation can be found over a much smaller geographical area (inset, Fig. 8).
Fig. 8 Simulated date of peak L4 occurrence over range of western spruce budworm in British Columbia, Canada. Circles are sample points used to test model. Inset displays complexity of spatial phenology over a relatively small area with pronounced elevational gradients.
Change in phenology between 1951 and 2012
Our model also indicates that a slight but highly significant change in seasonality (here, the date of maximum frequency of L4 in feeding populations) has occurred in BC over the last 60 years (Fig. 9). This shift of about 1.2 ± 0.3 days per decade (F 1,180 = 15.4, P < 0.001) towards earlier occurrence of successive life stages has proceeded at a similar rate in the three locations tested (F 2,180 = 0.1, P = 0.902; R 2 = 0.68) and represents slightly more than one week advance in phenology over the 62-year simulation period (1951–2012).
Fig. 9 Simulated date of peak L4 occurrence over the period 1951–2012 in three locations of interior British Columbia, Canada. Lines are regressions.
Discussion
Early phenology models for the western spruce budworm sought correlations between historical outbreaks and weather patterns (Thomson et al. Reference Thomson, Shepherd, Harris and Silversides1984; Kemp et al. Reference Kemp, Everson and Wellington1985; Williams and Liebhold Reference Williams and Liebhold1995). Thomson et al. (Reference Thomson, Harris, Silversides and Shepherd1983) used parameters derived from eastern spruce budworm in a degree-day model and then applied general lapse rates to account for the more variable phenology of western spruce budworm in the mountainous terrain of BC. This adjustment, however, did not produce accurate predictions for all life stages observed in field surveys nor was it equally applicable to all locations of interest. Kemp et al. (Reference Kemp, Dennis and Beckwith1986) also developed a degree-day model but with direct observations from field populations of western spruce budworm. Their model provided a good fit for each life stage but each year-by-plot combination required different parameters and so was unable to predict phenology in other locations or to simulate seasonality over the landscape. Recent climate-envelope models have the opposite problem in predicting only very coarse patterns over large landscapes (Murdock et al. Reference Murdock, Taylor, Flower, Mehlenbacher, Montenegro and Zwiers2013).
Compared to these predecessors, our individual-based, process-oriented phenology model provides robust predictions of western spruce budworm seasonality over a broad geographic range with sufficient precision to capture differences in age distributions, for example, along elevation gradients. The model captures many of the details noted in other phenology studies of Choristoneura budworms including sex-related, compensatory differences in rates of development of late instars and pupae (Volney and Liebhold Reference Volney and Liebhold1985; Lysyk and Nealis Reference Lysyk and Nealis1988; Régnière et al. Reference Régnière, St-Amant and Duval2012b) and protracted spring emergence (Volney et al. Reference Volney, Waters, Akers and Liebhold1983). The model produces accurate predictions of western spruce budworm phenology at broad spatial and temporal scales and can be used to address questions ranging from timing of stage-dependent management activities such as monitoring and insecticide applications to climate-driven changes in geographic distribution, host ranges, gene flow, and speciation.
Our model assumes that diapause termination in western spruce budworm occurs everywhere at the same fixed date of 1 March. This assumption is well justified throughout most of the budworm's range in the interior forests of the Pacific Northwest where winter temperatures rarely warm sufficiently for significant post-diapause development before that date. However, under mild maritime conditions of the Pacific coast, an earlier date might be assumed (Thomson and Benton Reference Thomson and Benton2007). A process-oriented model of spruce budworm diapause development, such as available for gypsy moth (Gray et al. Reference Gray, Ravlin and Braine2001), would be an informative extension of this model.
The efficacy of control options such as Btk depends upon application in a brief seasonal window; after most of the budworms are actively feeding but before they cause too much damage. The variable timing of western spruce budworm development at the landscape level and from year-to-year makes targeting this window especially challenging. A high-resolution phenology model such as reported here can be used to predict the location-specific distribution of age classes in real time (Régnière Reference Régnière1996) and provide decision support for pest management operations (Nealis et al. Reference Nealis, Régnière and Gray2001).
A process-oriented phenology model can also be used to explore more fundamental aspects of insect ecology and evolution. Phenology is critical to our understanding of species’ distributions (Chuine Reference Chuine2010) whether these distributions are limited directly by climate and weather or indirectly via stabilisation of life cycles (Powell and Logan Reference Powell and Logan2005). Population persistence and rates of change within the range may similarly be influenced directly by extreme weather events during susceptible life stages or via the degree of synchronisation of key trophic interactions. Thus, phenology models can be used to explore realistically the consequences of climate change on species range and population behaviour over a wide range of ecological scales (Régnière et al. Reference Régnière, St-Amant and Duval2012b). Historical changes in the apparent distribution of outbreaks of western spruce budworm (Thomson and Benton Reference Thomson and Benton2007; Nealis et al. Reference Nealis, Noseworthy, Turnquist and Waring2009) will be amenable now to more rigorous analysis.
Acknowledgements
The authors thank M. Noseworthy, R. Turnquist, N. Watson, and V. Waring for laboratory and field assistance; R. St-Amant and P. Duval for programming and mapping assistance. Lisa Lumley kindly provided original data for our analysis. They also thank B. Van Hezewijk and S. Magnussen for insightful comments on an earlier version of the manuscript.
