Impact statements
In decision making on flood risk management (FRM) uncertainties have to dealt with. In this article expertise from hydrology, statistics, communication and behavioral science is combined. This collaborative approach contributes to a better understanding of the various ways uncertainties are dealt with in decision making in FRM. Moreover, with this integration of expertise the article opens ways to strategies in which uncertainties are actually assimilated and adapted by decision makers in taking efficient decisions in (local) FRM.
Introduction
Flood risk management (FRM) aims to reduce the harm caused by flooding. In FRM, three sets of actions can be distinguished (Plate, Reference Plate2002). First, actions are needed to operate an existing system in an actual flood risk situation. Second, actions are needed to plan a new system or to revise an existing system to meet new needs and conditions. Following from this second action, a third set of actions is needed to obtain an optimum design for a new or revised system. In all three sets of actions, FRM deals with decision problems of varying complexity, characterized by varying types and levels of uncertainties that may or may not be statistically quantifiable. In this paper, we address the question of how to cope with these uncertainties, with a focus on the third set of actions: designing an optimal system. The key question is: how can uncertainties, whether statistically quantified or not, be dealt with to support efficient decision-making?
The aim of this paper is to propose the strategies to cope with uncertainties in a way that all possible kinds of uncertainty are named, recognized, statistically quantified as far as possible and utilized in efficient decision-making. For this purpose, we use the monster metaphor (Van der Sluijs, Reference Van der Sluijs2005; Smits, Reference Smits2006). We address the following questions:
-
1. What are the origins and guises of the various uncertainty monsters?
-
2. How are these monsters perceived by decision-makers?
-
3. Which coping strategies are available to “tame” the uncertainty monsters?
-
4. How do the choice between coping strategies depend on structure and complexity of decision problems?
-
5. Which coping strategies are preferred in efficient decision-making?
We show in a mock case on FRM how statistical knowledge on uncertainty can be adapted in order to enable efficient decision-making. We do not pretend to have solutions for complex decision problems with uncertainties. Nevertheless, with this paper, we hope to contribute to improved structure and reduced complexity of decision problems, which we consider as the key conditions for efficient decision-making in FRM. Besides the opportunities for utilization of statistical knowledge on uncertainty in decision-making, we also discuss the limitations.
Origins and guises of uncertainty monsters
The monster metaphor was developed by Smits (Reference Smits2006) to improve the understanding of risk controversies related to new technologies, based on the work of Douglas (Reference Douglas1966) on purity and danger in traditional cultures. The monster metaphor was introduced into the environmental sciences by Van der Sluijs (Reference Van der Sluijs2005). The basic idea is that if two categories that were considered to be mutually exclusive mix up, monstrous hybrids can grow. As Smits (Reference Smits2006) describes, these ambiguous phenomena can evoke feelings of fear or abhorrence, but also feelings of fascination and reverence. Van der Sluijs (Reference Van der Sluijs2005) considers the following mutually exclusive categories that create monsters in the science–policy interface: knowledge versus ignorance, objective versus subjective, facts versus values, prediction versus speculation and science versus policy. These categories can also be found in the area of FRM, where uncertainty monsters can appear at various places, including predictions or speculations on floods and their effects, risk awareness, support base and efficacy and efficiency of decisions. Some of these monsters spit out uncertainties that can more or less easily be statistically quantified. Other monsters spit out uncertainties that can only qualitatively be described. The existence of some monsters and the genesis of new monsters can only be suspected.
The guises of uncertainty monsters can vary. The most simple monster has one head that spits out statistically quantifiable uncertainty only. More complex species are multi-headed. The uncertainties that are spit out vary in space and time and can be mutually dependent. Nevertheless, they can still be quantified statistically although this can be complicated. These uncertainties are referred to as aleatory, which means that they are related to random processes that can be described in probabilistic terms. Besides aleatory uncertainties, epistemic uncertainties that are related to lack of knowledge can be distinguished. However, aleatory and epistemic uncertainty can be blurred, for example, Nearing et al. (Reference Nearing, Tian, Gupta, Clark, Harrison and Weijs2016) argue that most aleatory uncertainty at the scale of watersheds is also epistemic. It might be believed that all epistemic uncertainties can be reduced or eliminated by more accurate and detailed descriptions of hydrological systems. However, these efforts on model improvement can only concern known unknowns, while the existence of unknown unknowns cannot be excluded. Besides known and unknown unknowns, Di Baldassarre et al. (Reference Di Baldassarre, Brandimarte and Beven2016) distinguish wrong assumptions: things we think we know, but we actually do not know. Efforts can be made to represent epistemic uncertainty probabilistically (Montanari and Koutsoyiannis, Reference Montanari and Koutsoyiannis2012). However, it cannot be ruled out that deep uncertainties remain that cannot be expressed in probabilistic terms, also referred to as Knightian uncertainties (Knight, Reference Knight1921) or surprises (Brown, Reference Brown2004; Merz et al., Reference Merz, Sergiy Vorogushyn, Viglione and Blöschl2015).
Brown (Reference Brown2004) defines uncertainty as a state of confidence in knowledge, varying between being certain and accepting that we cannot know, that is indeterminacy. In this definition, confidence is a state of awareness of imperfect knowledge. Ignorance is defined as lack of awareness of imperfect knowledge. Further, Brown (Reference Brown2004) distinguishes “bounded” and “unbounded” uncertainty. “Bounded” means that all possible outcomes are known, but not necessarily all corresponding probabilities. Uncertainty is “unbounded” when some possible outcomes are known, possibly with corresponding probabilities, or when no possible outcomes are known.
Perceptions and behavioral consequences of uncertainty monsters
In the above, we have described that the uncertainty monster may come in different forms and shapes. The guises of the uncertainty monster can influence the perceptions of uncertainties and risks and the ways in which the uncertainty monster is dealt with. The risk perception literature describes that people are subject to forming overall risk perceptions on the basis of various cues (Slovic et al., Reference Slovic, Finucane, Peters and MacGregor2004). One of them is the extent to which (possible) events are viewed to be dreadful – that is, having catastrophic potential, affecting many people and so forth. Another is the experienced level of uncertainty – is it a phenomenon known to science, is it a novel event, and so forth. Typically, individuals rely on such cues in forming perceptions, and cues inform human decision-making, too.
Relying just on contextual cues – or heuristics – may, however, lead to faulty or suboptimal decisions (Kahneman, Reference Kahneman2011). In particular when decision problems are complex in nature, it may be important to process information with logic and reason. Humans are equipped with an analytical system to perform such information processing. However, individuals can also process information with the use of the so-called experiential system. In this case, affect and intuition play a more dominant role in the processing of information and in reaching a decision.
In some cases, individuals may be very aware of risks but still deny it. Denial may be a coping mechanism, and may be brought about when people do not see a clear behavioral pathway to deal with the risk – that is, they lack a sense of efficacy (Maddux and Rogers, Reference Maddux and Rogers1983). In the financial realm, the denial of a risk that one is actually aware of is coined the ostrich effect (Karlsson et al., Reference Karlsson, Loewenstein and Seppi2009). It may also lead to avoiding the search for additional information that could actually help to better understand the risk problem. Another example of how individuals can deal with an uncertainty monster is by continuing to put resources into endeavors that are not likely to be successful, or at least break even the investment made. This can lead to an ironic effect of people clinging on to projects that have limited viability, but given the amount of investments that were already made it is considered a “waste” to abandon the project – a phenomenon called the sunk cost fallacy or Concorde effect (Arkes and Ayton, Reference Arkes and Ayton1999).
There are examples of the Concorde effect in natural flood management (NFM), in which efficacy is at times blown out of proportion (Bokhove et al., Reference Bokhove, Hicks, Kent and Kelmanson2021), in part because it is challenging to assess at a strategic or policy level (Environment Agency, 2022). In particular, lack of upscaling potential of NFM to intermediate and large floods remains an issue, leading to a blended approach that aims to place different types of flood mitigation measures in the right places (Environment Agency, 2021c). Proposing flood storage due to beaver dams is an extreme example; it is officially mentioned in government reports (DEFRA, 2018) without mentioning the lack of upscaling potential (Bokhove et al., Reference Bokhove, Kent and Kelmanson2018) or international viewpoints thereon. The available flood-storage volume behind perfect beaver dams tends to be very small, such that 1,000s–10,000s beaver colonies would be needed to prevent intermediate to larger floods, which remains unrealistic even for 1% coverage. Furthermore, potential dam collapse (Hillman, Reference Hillman1998; Butler and Malanson, Reference Butler and Malanson2005) and lack of planned maintenance are sources of uncertainty. In contrast, in the Netherlands, the 1,000s of beavers roaming the countryside are valued for their local wildlife value, for example, in terms of locally improving water quality and creating wetland habitat, but beavers are deemed destructive with respect to flood mitigation, since they seriously undermine protective berms and dikes. The involved stakeholders (province, water authorities, nature conservation managers and other actors) were increasingly aware of the risks as well of their specific responsibilities toward flood protection and nature conservation, which resulted in a joint policy established in a beaver protocol (Heijer et al., Reference Heijer, Rijke, Bosch-Rekveldt, de Leeuw and Barciela-Rial2023).
On the one hand, here we have argued that an uncritical reliance on uncertain benefits is related to the Concorde effect if one takes account of social and emotional investments. On the other hand, the counter-argument would be that decades of investment of large amounts of public money (and carbon, political capital, etc.) on hard infrastructure may be a Concorde effect in some places, for example, for 149–185 km of the U.K. coastline where protecting or adapting as currently planned appears to be economically unfeasible (CCC, 2018). In either case, it is important to understand both the ongoing benefits and residual risks arising from past investments, and a failure to assimilate the associated uncertainties may provide a platform for pathological monster coping strategies discussed in the following sections.
In analyzing the role of uncertainty in FRM, it is important to be aware of the bounded rationality of human decision-making. This is not to say that humans are irrational, but their rationality is bounded by an array of perceptual and motivational phenomena that may impact or bias behavior (Simon, Reference Simon, Eatwell, Milgate and Newman1990). Given the simple fact that in FRM the stakes are high, it is crucial to adopt a structured and systematic approach toward decision problems. Before doing so, we will first describe the various ways uncertainty in decision-making may be dealt with.
Coping strategies
Van der Sluijs (Reference Van der Sluijs2005) mentioned four possible strategies to cope with the monster of uncertainty: monster exorcism, monster adaptation, monster assimilation and monster embracement. We summarize our interpretations of these strategies and we add monster denial and monster anesthesia to them.
In monster exorcism, it is tried to reduce uncertainty to zero. However, zero uncertainty is unreachable since knowledge is limited, reality is necessarily generalized in models, sample sizes are limited and observations have limited accuracy. Monster adaptation transforms the monster into a phenomenon that fits in the aforementioned categories. This is attempted by quantifying uncertainty to support rational risk management on the basis of optimization of expected utility. Bluntly said, the decision is the outcome, or at least supported by the outcome of calculations. However, uncertainties are not always quantifiable, sometimes hidden, and have sometimes not arisen yet.
Monster embracement can possibly be related to a fascination for the complexity of environmental systems. However, magnification of uncertainties can also be a strategy to trivialize unpleasant outcomes of scientific research.
Monster assimilation differs from monster adaptation in that not only the monster is adapted, but also the mutually exclusive categories that were mixed up, such as science and policy. These categories are assumed to be flexible enough to learn from uncertainty and to change. In monster assimilation a central place is given to uncertainties in environmental risk management. The idea of one certain truth is dropped. Parties involved in risk assessment strive for transparency and learn to live with ambiguity and pluralism.
To the four coping strategies described above, we add two strategies to cope with unwelcome uncertainty: monster denial and monster anesthesia. Van der Sluijs (Reference Van der Sluijs2005) considers the strategy of hiding unwelcome uncertainty as a case of monster exorcism. However, for monster exorcists, uncertainty can be welcome, because it legitimates their efforts to improve deterministic models. Information on uncertainty can be unwelcome for several reasons, in policy as well as in science (see, for instance, Pappenberger and Beven, Reference Pappenberger and Beven2006). They discussed seven possible reasons why uncertainty analysis is not performed in hydrological and hydraulic modeling by a significant part of the professional community, and concluded that none of these seven reasons are, in the end, tenable. Not mentioning or even denying can be a strategy in these cases. Another strategy to deal with unwelcome uncertainty is striving for consensus in the deliberations of supervisory committees. An agreement about the quality of information does not imply that uncertainty is expelled, however. After the deliberations, the unwelcome uncertainty monster sleeps.
Levels of complexity and structure in decision-making
In a discussion on the place of uncertainty in FRM, it makes sense that decision problems can vary in complexity and structure (see Figure 1). A complex decision problem has many components. We consider ambiguity as part of the complexity of a decision problem: different parties may think differently about the causes and effects of risks (interpretive ambiguity), and about what actions are justified once risks are characterized (normative ambiguity) (Renn, Reference Renn2008). Besides complex, decision problems can be poorly structured. We relate structure to the conditions under which decisions are made. Poor structure can make decision problems appear more complex than they actually are. Turnhout et al. (Reference Turnhout, Hisschemöller and Eijsackers2007)) distinguish unstructured, badly structured, moderately structured and well-structured decision problems. In these categories, knowledge is used by means of ideas, concepts, arguments and data, respectively. The roles of scientists are problem signaling, accommodation, advocacy and problem solving, respectively. At best, the policy process can result in learning, finding compromises, negotiation and taking formal decisions, respectively.

Figure 1. Decision problems categorized into levels of complexity and structure, as well as strategies to cope with uncertainty.
The levels of complexity and structure determine which strategy can be chosen to tame the uncertainty monsters (Poortvliet et al., Reference Poortvliet, Knotters, Bergsma, Verstoep and van Wijk2019). In the following section, we argue why monster adaptation and monster assimilation should be strived for to enable efficient decision-making, and monster embracement, exorcism, denial and anesthesia should be avoided. This implicates that decision problems should be structured as well as possible, and be simplified as far as possible. These aims are indicated with the blue, dashed arrows in Figure 1.
Preferred coping strategies: Monster adaptation and monster assimilation
Monster exorcism, monster denial and monster anesthesia can be seen as strategies sprouting from “certainification”: striving for certainty (Van Asselt et al., Reference Van Asselt, Mesman and Van‘t Klooster2007). Although it is acknowledged that certainification enables practitioners to proceed, Van Asselt et al. (Reference Van Asselt, Mesman and Van‘t Klooster2007) question whether this is a sustainable strategy in the long run. For instance, the public can lose trust in policy makers if things went out in a different way than was told. Whereas in controversies, decision-makers tend to certainification, the strategy of opponents can be “decertainification” (monster embracement). To reduce risks of cumbersome decision processes, we prefer monster assimilation and wherever possible monster adaptation above the certainifying strategies of monster exorcism, monster denial and monster anesthesia and decertainifying monster embracement. Besides this, it can be more efficient to take quantified uncertainty into account rather than to make costs to reduce uncertainty (Morgan and Henrion, Reference Morgan and Henrion1990). Therefore, we recommend quantitative uncertainty and risk analysis, that is, monster adaptation rather than monster exorcism, as will become clear in the examples we will consider next. Monster adaptation is possible if uncertainties can be quantified, that is, bounded uncertainties with all probabilities known (Brown, Reference Brown2010). If some or all uncertainties can be described qualitatively only, we prefer monster assimilation as a coping strategy in decision-making. The perceptual model of uncertainty as described by Westerberg et al. (Reference Westerberg, Di Baldassarre, Beven, Coxon and Krueger2017) can be helpful in monster adaptation and assimilation. Westerberg et al. (Reference Westerberg, Di Baldassarre, Beven, Coxon and Krueger2017) illustrated a three-step procedure to construct a perceptual uncertainty model with an example on flood risk change. The three steps include (1) identifying uncertainty in the framing of the studied system and problem, (2) identifying the uncertainty sources in the socio-hydrological system and (3) defining the nature, interactions and relative importance of the uncertainty sources.
These two preferred coping strategies emerging in the FRM practice are exemplified next in three ways, which involve:
-
A. adaptation to aleatory uncertainty through the design flood concept;
-
B. assimilation through recognition of epistemic uncertainties in flood hydrology; and,
-
C. adaptation and assimilation intertwined in a mock pluvial flood-mitigation case study wherein several scenarios are juxtaposed using a graphical cost-effectiveness tool.
A. Monster adaptation: Aleatory uncertainty and the design flood concept
Although direct, systematic observations of precipitation and river flows have been made in some places since at least the 17th century (Deming, Reference Deming2021), it was the development of mathematical theory about the statistics of extremes that enabled a coherent, quantitative approach to flood risk analysis. In the United States, Dawdy et al. (Reference Dawdy, Griffis and Gupta2012)) reported that statistical analysis of flooding started with Fuller (Reference Fuller1914), who advocated that “study of their [floods] past frequency gives the best indication of what may be expected in the future” (although Robert Horton had applied probability analysis to plot flood data on logarithmic paper since 1896).
By the mid-20th century, the theoretical foundations for probabilistic analysis of flooding were growing stronger with pioneering work by Gumbel (Reference Gumbel1958) on extreme value theory, which included analysis of “the design flood,” amongst other applications in climatology, meteorology and hydrology.
Aided by extreme value theory, the concept of a statistical design flood effectively internalized aleatory uncertainty by simplifying the flood-protection decision problem to one of selecting an appropriate tail quantile of the flood distribution to reflect a chosen tolerance of risk. This internalization has proven to be a lasting and important form of monster adaptation, even though some did object to it, exemplified by T. Merriman’s statement in the 1926 Transactions of the American Society of Civil Engineers that flooding could not be “fairly treated by any method of probabilities” (Dawdy et al., Reference Dawdy, Griffis and Gupta2012), arguably a case of determinism leading to monster exorcism.
By the late 1960s and early 1970s, statistical analysis of river flow extremes was an established tool for hydrologists and engineers. Even so, hydrologists were aware of epistemic uncertainties, with the choice of statistical distribution being both an important practical question and a lively topic of research ever since (Benson, Reference Benson1968; Bobée et al., Reference Bobée, Cavadias, Ashkar, Bernier and Rasmussen1993; Vogel et al., Reference Vogel, McMahon and Francis1993a, Reference Vogel, Thomas and McMahon1993b; Kochanek et al., Reference Kochanek, Renard, Arnaud, Aubert, Lang, Cipriani and Sauquet2014). In a global meta-review by Diaconu et al. (Reference Diaconu, Costache and Popa2021)), 20% of 1,326 research papers about flood risk analysis methodology published between 1979 and 2020 concerned statistical analysis. Detailed guidance emerged for practical applications in which choices about statistical distributions and procedures for assessing data adequacy were considered (NERC, 1975; Institute of Hydrology, 1999; Ball et al., Reference Ball, Babister, Nathan, Weeks, Weinmann, Retallick and Testoni2019; England Jr et al., Reference England, Cohn, Faber, Stedinger, Thomas, Veilleux, Kiang and Mason2019). In Europe, Castellarin et al. (Reference Castellarin, Kohnova, Gaal, Fleig, Salinas, Toumazis, Kjeldsen and Macdonald2012) found that public agencies and institutions of six countries provide guidance about statistical distributions suitable for flood hydrology, while national statistical analyses of flood peaks exist in 12 of the 18 countries surveyed.
Deterministic models of flood hydrology have been used in estimating design floods since at least the development of unit hydrograph theory (Sherman, Reference Sherman1932; Clark, Reference Clark1945; Dooge, Reference Dooge1973). Eagleson (Reference Eagleson1972) showed how aleatory uncertainty about rainfall extremes, embedded in a statistical model, could be integrated analytically with a deterministic model of rainfall–runoff dynamics to derive a flood peak flow distribution. In our monster analogy, this physically motivated reasoning can be interpreted as an attempt to address epistemic uncertainty about the representation of complex hydrological processes that may have otherwise been ignored (monster denial). Subsequently, many combinations of stochastic weather models and deterministic hydrological system models have been proposed or applied to support flood risk analysis (Boughton and Droop, Reference Boughton and Droop2003; Lamb, Reference Lamb and Anderson2006). Primary motivations for the rainfall–runoff approaches were to incorporate knowledge about hydrological processes into design flood estimation (Lamb et al., Reference Lamb, Faulkner, Wass and Cameron2016), and to take advantage of both river flow data and precipitation measurements, which can be longer and spatially denser. Aleatory uncertainty in the rainfall or river flow data remained the dominant guise of the uncertainty monster, with the target remaining a design event.
B. Monster assimilation: Recognition of epistemic uncertainties in flood hydrology
The introduction of process-based modeling to derive design flows was at first motivated by a desire to reduce uncertainty by applying deterministic understanding of processes to add information in deriving a design flood. Yet opening the door to physical processes inevitably exposes the decision analysis to complexities of the real world, where it is difficult to find simple adaptations to uncertainty monsters. In flood management, and across other natural hazards, there has been an increasing focus on the epistemic uncertainties, which are not well-determined by historical observations (Beven et al., Reference Beven, Almeida, Aspinall, Bates, Blazkova, Borgomeo, Freer, Goda, Hall, Phillips, Simpson, Smith, Stephenson, Wagener, Watson and Wilkins2018). Where the uncertainties can be expressed in terms of input factors or choices made in applying a model, then sensitivity analysis is a powerful tool to structure and quantify a wide range of sources of uncertainty (Pianosi et al., Reference Pianosi, Beven, Freer, Hall, Rougier, Stephenson and Wagener2016; Gupta and Razavi, Reference Gupta and Razavi2018; Wagener and Pianosi, Reference Wagener and Pianosi2019; Pianosi et al., Reference Pianosi, Sarrazin and Wagener2020).
Quantification is difficult, or may be impossible, for deep epistemic uncertainties (Stein and Stein, Reference Stein and Stein2013), so the uncertainty monster appears in guises that are not amenable to monster adaptation. Instead, we try to assimilate those monsters to avoid the pathological states of embracement, exorcism, denial or anesthesia. Environmental or socioeconomic change is often the dominant uncertainty for long-term FRM planning. A typical paradigm for assimilating such deep uncertainty monsters is to use scenario-based analysis (Hallegatte et al., Reference Hallegatte, Shah, Lempert, Brown and Gill2012), an approach formalized for national FRM investment planning in England by the Environment Agency (2021b). Future projections of risk are needed for scenario-based decision analysis, but growing evidence of historical changes in flooding (Blöschl et al., Reference Blöschl, Hall, Viglione, Rui, Parajka, Merz, Lun, Arheimer, Aronica, Bilibashi, Boháč, Bonacci, Borga, Čanjevac, Castellarin, Chirico, Claps, Frolova, Ganora, Gorbachova, Gül, Hannaford, Harrigan, Kireeva, Kiss, Kjeldsen, Kohnová, Koskela, Ledvinka, Macdonald, Mavrova-Guirguinova, Mediero, Merz, Molnar, Montanari, Murphy, Osuch, Ovcharuk, Radevski, Salinas, Sauquet, Šraj, Szolgay, Volpi, Wilson, Zaimi and Živković2019; Environment Agency, 2020; Hannaford et al., Reference Hannaford, Mastrantonas, Vesuviano and Turner2021; Slater et al., Reference Slater, Villarini, Archfield, Faulkner, Lamb, Khouakhi and Yin2021) has also challenged the assumption of stationarity that has been inherent in most statistical flood models. Practical guidance on the incorporation of nonstationary extreme value analysis is now appearing for flood analysts (US Army Corps of Engineers, 2018; Ryberg et al., Reference Ryberg, Kolars, Kiang and Carr2020; Environment Agency, 2021a), enabling uncertainty relating to the choice of an appropriate baseline to be quantified within a decision analysis.
For example, in JBA Consulting (2022) (Section 6), a decision analyst’s choice between adopting a stationary or nonstationary model for river flow extremes was framed as an epistemic uncertainty in the design of an idealized flood management scheme. The implications were investigated by assessing the sensitivity of the scheme design to this choice between models, using a method outlined in Figure 2, adapted from Rehan (Reference Rehan2016) and Rehan and Hall (Reference Rehan and Hall2016). Context was provided by basing the idealized case on a real flood management scheme, and adding a comparison with a second source of epistemic uncertainty, represented by contamination of the gauged flow data with hydrometric measurement errors that were introduced artificially for the purposes of the experiment. The three possible inputs are plotted in Figure 3. The models adopted for the flood peaks were generalized logistic distributions, which are widely used in U.K. flood hydrology. Sensitivity of the design with respect to these input choices was studied by simulating an FRM economic appraisal to minimize the total present value cost with respect to the design height of the scheme’s flood defense. Monte Carlo simulation (MCS) was used to account for sampling uncertainty about the flood peak distribution for comparison with the epistemic uncertainties.

Figure 2. Schematic of flood risk management (FRM) decision simulation by JBA Consulting (2022). Economic relationships for the scheme costs and flood damages are combined with models for the extreme value distribution of peak river flows and the hydraulic model outputs relating flows and flood depths. The choice between a stationary or a nonstationary flood peak model is represented as an epistemic uncertainty, as is the effect of artificially introducing errors to the gauged flows. Parameters of the peak flow model are sampled randomly in a Monte Carlo simulation to allow the epistemic uncertainties to be compared with aleatory uncertainty related to the sampling of the gauged flows.
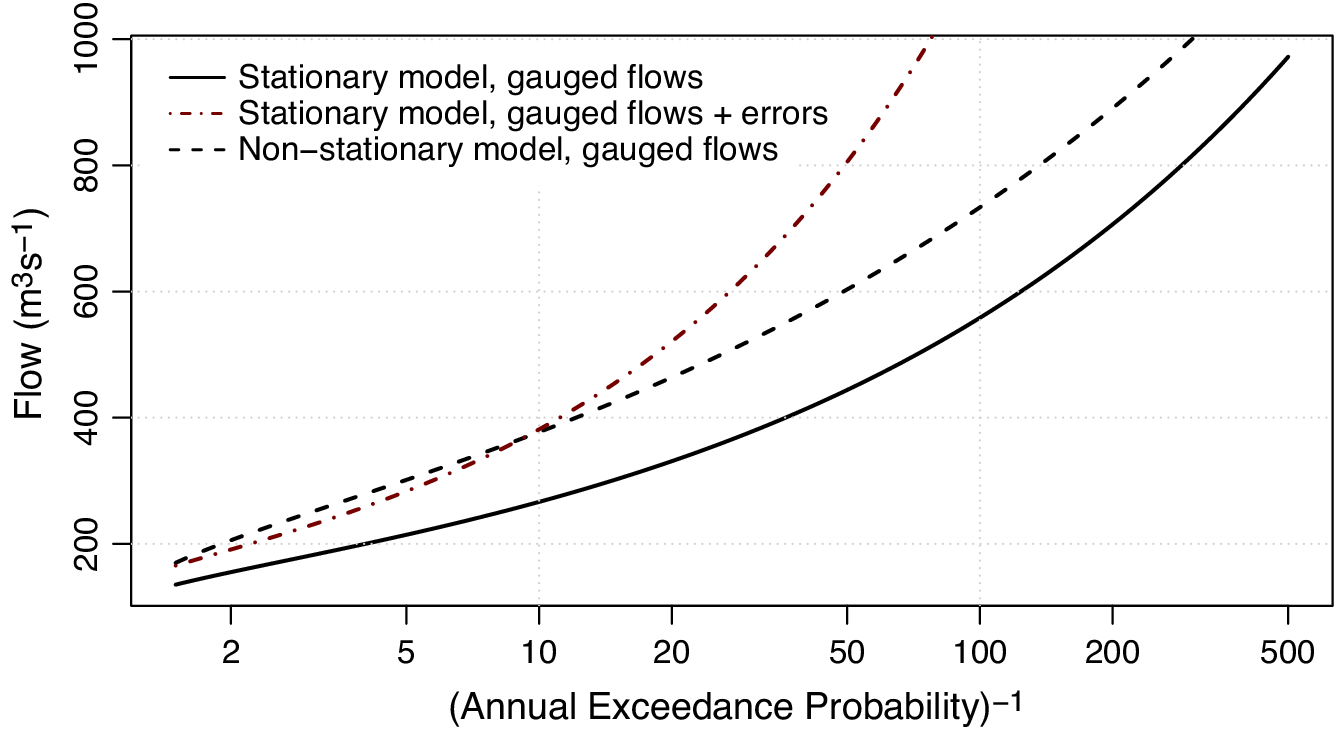
Figure 3. Inputs to the flood risk management (FRM) decision simulation shown in Figure 2 as epistemic uncertainties. The curves are generalized logistic distributions, which are adopted as extreme value models for the peak flows. The choices available to the analyst are a stationary model fitted to gauged peak flows, a stationary model fitted after errors were added to the gauged flow data, and a nonstationary model fitted to gauged flows (evaluated for 2016, taken to be the year of the decision analysis).
Results of the simulation in Figure 4 show that the adoption of a nonstationary model for the flood peak distribution would make a substantial difference to the idealized scheme design. This impact was larger than the effect of the second counterfactual case, in which errors were added to the peak flow data as a confounding uncertainty, and distinguishable from the sampling uncertainty as indicated by the interquartile range obtained by MCS.

Figure 4. Results of the flood risk management (FRM) decision simulation outlined in Figure 2, showing the economically optimum defense height, with uncertainties estimated by drawing 1,000 samples from the covariance matrices of generalized logistic distribution parameters fitted to the peak river flows. Panels show the results for different combinations of input factors. Comparison of panels (a) and (b) reveals epistemic uncertainty about the choice between a stationary and nonstationary model for the peak flows. Panel (c) simulates the effect of adding data errors to the stationary model for comparison. Plotted using R v4.2.0 boxplot function with default options: shaded boxes represent interquartile range (IQR), interior thick line is median, interior dot is mean, open circles are outliers and whiskers extend to a maximum of 1.5xIQR beyond the box (see function documentation for further details and Krzywinski and Altman, Reference Krzywinski and Altman2014 for interpretation).
Statistical models applied routinely in U.K. flood management practice have usually been predicated on stationarity assumptions. However, recent guidance (Environment Agency, 2021a) describes situations in which a nonstationary model may be preferred to inform the planning and economic appraisal of FRM schemes. The guidance requires analysts to apply judgment after taking account of different analytical approaches, which raises a need for the type of epistemic uncertainty assimilation that is illustrated in the case study.
Similar uncertainties arise in the context of land use change. This is both a historical issue, in terms of its influence on observed flood data, and an uncertainty in evaluating future flood management actions that involve nature-based solutions (NBS, also called working with natural processes, and including NFM). With rapidly growing interest worldwide in the potential of NBS to deliver multiple co-benefits (Iacob et al., Reference Iacob, Rowan, Brown and Ellis2014; Seddon et al., Reference Seddon, Chausson, Berry, Cécile, Smith and Turner2020), uncertainties about the effects of land management changes on flooding have received considerable attention (Dadson et al., Reference Dadson, Hall, Murgatroyd, Acreman, Bates, Beven, Heathwaite, Holden, Holman, Lane, O’Connell, Penning-Rowsell, Reynard, Sear, Thorne and Wilby2017; Lane, Reference Lane2017; Möller, Reference Möller2019; Ellis et al., Reference Ellis, Anderson and Brazier2021). Some modeling studies have attempted to capture uncertainties about land use changes through conditional probabilistic approaches to the inference of shifts in the parameters of deterministic models (Hankin et al., Reference Hankin, Trevor, Chappell, Beven, Smith, Kretzschmar and Lamb2021; Beven et al., Reference Beven, Page, Hankin, Smith, Kretzschmar, Mindham and Chappell2022), although there may be residual risks associated with some systems of NBS (Hankin et al., Reference Hankin, Hewitt, Sander, Danieli, Formetta, Kamilova, Kretzschmar, Kiradjiev, Wong, Pegler and Lamb2020). Controversy about the effectiveness of NBS for FRM (Ellis et al., Reference Ellis, Anderson and Brazier2021) can also be rooted in uncertainties, a form of monster embracement such as that documented by Turnhout et al. (Reference Turnhout, Hisschemöller and Eijsackers2008) in two controversies regarding cockle fisheries and gas mining in the Wadden Sea (an estuarine area with high ecological potential), where scientific uncertainties were exploited by competing stakeholders to undermine each other’s claims.
When confronted with deep uncertainties and knowledge controversies, one strategy that may help to navigate a path from pathological monster coping strategies toward assimilation is expert elicitation. Structured, performance-weighted elicitation has been shown in many applications to add decision- or policy-relevant information (Colson and Cooke, Reference Colson and Cooke2018). Good elicitation practice requires skill, resources and care; it is not a low-cost alternative to research or analysis (Morgan, Reference Morgan2014), and can surface meta-uncertainties related to cognitive biases (Morgan, Reference Morgan2014) or methodological choices (Clemen, Reference Clemen2008). By conditioning expert judgments against calibration questions (for which uncertainty ranges are known objectively) and pooling multiple expert views, it is possible to obtain probabilistic statements from an elicitation (Aspinall and Cooke, Reference Aspinall, Cooke, Rougier, Hill and Sparks2013). In the case of scour damage to bridges caused by river flooding, Lamb et al. (Reference Lamb, Aspinall, Odbert and Wagener2017) demonstrated an elicitation approach to deriving scour failure probabilities (similar to the uncertain failure probabilities in our case study in Section 5C) by applying the method of Cooke (Reference Cooke1991).
C. Monster assimilation and adaptation: Fluvial flood-mitigation case study
We introduce a mock or hypothetical flood-mitigation study on pluvial or surface flooding in a local neighborhood to highlight decision-making challenges in FRM. The study fits in the middle of the monster-metaphor schematic of Figure 1, as it is of intermediate complexity but some uncertainties are difficult to quantify. It is inspired by an actual case. The study will employ a graphical cost-effectiveness tool, see Bokhove et al. (Reference Bokhove, Kelmanson, Kent, Piton and Tacnet2019) and Bokhove (Reference Bokhove2021), which has successfully engaged decision-makers in France and Slovenia (see Piton et al., Reference Piton, Dupire, Arnaud, Mas, Marchal, Moncoulon, Curt and Tacnet2018a, Reference Piton, Pagano, Basile, Cokan and Lesjak2018b; Bokhove et al., Reference Bokhove, Hicks, Kent and Kelmanson2021; Bokhove et al., Reference Bokhove, Kelmanson, Piton and Tacnet2024). First, fluvial flooding of the neighborhood can be caused by the adjacent river and the outflow of the stream or brook “High Beck” into that river is closed off at higher river levels. Newly built flood walls aim to protect against fluvial events with return periods of
![]() $ 1:200\mathrm{yrs} $
. Second, High Beck has caused intermittent pluvial or surface flooding for decades, regarding beck-flooding events with return periods of
$ 1:200\mathrm{yrs} $
. Second, High Beck has caused intermittent pluvial or surface flooding for decades, regarding beck-flooding events with return periods of
![]() $ 1:10\mathrm{yrs} $
or higher. To avoid increased surface flooding when the beck cannot flow into the river, a pump with a maximum rate of QT = 0.245 m3/s has been installed. Hence, without further interventions, the intermittent surface-flooding events remain. The stream or beck has a length of circa 2,000 m with a drop of circa 100 m. Upstream of the outflow into the river, the beck passes under a canal in a nearly horizontal 200 m-long culvert passing under playing fields to the river, which culvert floods the neighborhood in extreme beck events. The relevant canal segment has a large size of 7.5 km × 10 m × 1.5 km with several overflow weirs to the river.
$ 1:10\mathrm{yrs} $
or higher. To avoid increased surface flooding when the beck cannot flow into the river, a pump with a maximum rate of QT = 0.245 m3/s has been installed. Hence, without further interventions, the intermittent surface-flooding events remain. The stream or beck has a length of circa 2,000 m with a drop of circa 100 m. Upstream of the outflow into the river, the beck passes under a canal in a nearly horizontal 200 m-long culvert passing under playing fields to the river, which culvert floods the neighborhood in extreme beck events. The relevant canal segment has a large size of 7.5 km × 10 m × 1.5 km with several overflow weirs to the river.
The council is exploring flood-mitigation measures against the surface flooding, as follows:
(C1) The beck flow gets diverted into the canal instead of being channeled under the canal (C1). An extra canal-river overflow will be built as well as an automated gate to divide water into canal and/or culvert. Costs
![]() $ {q}_1 $
.
$ {q}_1 $
.
![]() $ (B2 $
) Far upstream, bunds (B2) are built at a few flatter areas to slow the beck’s flow during severe rainfall. The bunds partially prevent the downstream surface flooding. Costs
$ (B2 $
) Far upstream, bunds (B2) are built at a few flatter areas to slow the beck’s flow during severe rainfall. The bunds partially prevent the downstream surface flooding. Costs
![]() $ {q}_2 $
.
$ {q}_2 $
.
![]() $ ( FP3 $
) The culvert from canal to river will be opened up with playing fields acting as flood-plain storage (
$ ( FP3 $
) The culvert from canal to river will be opened up with playing fields acting as flood-plain storage (
![]() $ FP3 $
) and protective bunds are built. Costs
$ FP3 $
) and protective bunds are built. Costs
![]() $ {q}_3 $
.
$ {q}_3 $
.
Measures B2 and FP3 offer insufficient protection in separation against the design flood but five permissible scenarios: C1, B2+FP3, B2+C1, FP3+C1 and B2+FP3+C1, do offer protection against 150 years return-period beck floods modeled using intense 3 h rainfall events. Except when C1 is fully used, scenarios with outflow into the river do require prolonged pumping of beck flood waters over the flood-defense wall into the river, for up to 10 h.
The following monster risks emerge:
(M1) There is a fear of berm collapse of the Victorian-age canal
![]() $ C1 $
. Breaches can occur at two weaker spots and would lead canal waters through fields to the river. However, berm collapse is already a fear to-be-dealt-with during heavy rainfall periods when the canal fills from its uphill side. Failure probability
$ C1 $
. Breaches can occur at two weaker spots and would lead canal waters through fields to the river. However, berm collapse is already a fear to-be-dealt-with during heavy rainfall periods when the canal fills from its uphill side. Failure probability
![]() $ {p}_1 $
and damage
$ {p}_1 $
and damage
![]() $ {q}_{p_1} $
were a priori unknown. Both fear and ignorance combine in M1.
$ {q}_{p_1} $
were a priori unknown. Both fear and ignorance combine in M1.
(M2) The new upstream bunds for
![]() $ B2 $
may fail with failure probability
$ B2 $
may fail with failure probability
![]() $ {p}_2<{p}_1 $
but failure can lead to a flood wave of the beck into urban areas with potential for a lot of damage, given the steep slopes, carrying an estimate damage
$ {p}_2<{p}_1 $
but failure can lead to a flood wave of the beck into urban areas with potential for a lot of damage, given the steep slopes, carrying an estimate damage
![]() $ {q}_{p_2} $
, both a priori unknown. Ignorance enters M2.
$ {q}_{p_2} $
, both a priori unknown. Ignorance enters M2.
(M3) The bunds lying in the playing fields for
![]() $ FP3 $
may fail with low probability
$ FP3 $
may fail with low probability
![]() $ {p}_3<{p}_2<{p}_1 $
and each flooding event requires a clean-up of deposited debris; costs
$ {p}_3<{p}_2<{p}_1 $
and each flooding event requires a clean-up of deposited debris; costs
![]() $ {q}_{p_3} $
. This monster is one of fear of and opposition against intermittent pollution of the public playing fields.
$ {q}_{p_3} $
. This monster is one of fear of and opposition against intermittent pollution of the public playing fields.
(M4) Subjective rejections or co-benefits of options can become monsters or fairies. For example, the canal has ecological value and cannot be used for flood protection (according to some); feeding the canal with beck water offsets droughts (a co-benefit) and, hydrographs, probabilities and costs include uncertainty. How do we value such monsters and fairies in the decision-making process?
Costs
![]() $ {q}_1,{q}_2,{q}_3 $
are known. Probabilities
$ {q}_1,{q}_2,{q}_3 $
are known. Probabilities
![]() $ {p}_1,{p}_2,{p}_3 $
and costs
$ {p}_1,{p}_2,{p}_3 $
and costs
![]() $ {q}_{p_1},{q}_{p_2},{q}_{p_3} $
over the entire 25 years write-off period were unknown a priori but have been estimated through expert elicitation, a scientific consensus methodology (Aspinall and Cooke, Reference Aspinall, Cooke, Rougier, Hill and Sparks2013).
$ {q}_{p_1},{q}_{p_2},{q}_{p_3} $
over the entire 25 years write-off period were unknown a priori but have been estimated through expert elicitation, a scientific consensus methodology (Aspinall and Cooke, Reference Aspinall, Cooke, Rougier, Hill and Sparks2013).
For a design-flood event with a
![]() $ 1:50\mathrm{yrs} $
return period or an annual event probability of
$ 1:50\mathrm{yrs} $
return period or an annual event probability of
![]() $ 2\% $
the beck’s flood hydrograph is shown in Figure 5. Flooding occurs for discharges above the threshold
$ 2\% $
the beck’s flood hydrograph is shown in Figure 5. Flooding occurs for discharges above the threshold
![]() $ {Q}_T $
. The flood-excess-volume (FEV) responsible for the flood damage is then the time-integrated discharge excess
$ {Q}_T $
. The flood-excess-volume (FEV) responsible for the flood damage is then the time-integrated discharge excess
![]() $ Q\left(\mathrm{t}\right)-{Q}_T $
over time
$ Q\left(\mathrm{t}\right)-{Q}_T $
over time
![]() $ t $
, with the event starting at
$ t $
, with the event starting at
![]() $ t={t}_0 $
and ending at
$ t={t}_0 $
and ending at
![]() $ t={t}_0+T $
:
$ t={t}_0+T $
:
 $$ FEV={\int}_{t_0}^{t_0+T}\left(Q(t)-{Q}_T\right)\;\mathrm{d}t\approx 9600{\mathrm{m}}^3\approx 98\mathrm{m}\hskip0.24em \times 98\mathrm{m} \times 1\mathrm{m}, $$
$$ FEV={\int}_{t_0}^{t_0+T}\left(Q(t)-{Q}_T\right)\;\mathrm{d}t\approx 9600{\mathrm{m}}^3\approx 98\mathrm{m}\hskip0.24em \times 98\mathrm{m} \times 1\mathrm{m}, $$
reexpressed as a (dynamic) square lake of 1 m depth. This High-Beck FEV-lake is large, given the size of the neighborhood. Displaying FEV as a 1 m-deep lake therefore adds a sense of size to a flooding event, with 1 m being (half) a human-size scale.

Figure 5. Hydrograph of a simulated 150 years return-period design flood-event of High Beck, displaying discharge
![]() $ Q(t) $
versus time
$ Q(t) $
versus time
![]() $ t $
with
$ t $
with
![]() $ 5\% $
error bars indicated as dotted lines. The integrated discharge above the flooding threshold
$ 5\% $
error bars indicated as dotted lines. The integrated discharge above the flooding threshold
![]() $ {Q}_T=0.245{\mathrm{m}}^3/\mathrm{s} $
constitutes the flood-excess volume, here
$ {Q}_T=0.245{\mathrm{m}}^3/\mathrm{s} $
constitutes the flood-excess volume, here
![]() $ FEV\approx 9600{\mathrm{m}}^3 $
, causing the flood damage.
$ FEV\approx 9600{\mathrm{m}}^3 $
, causing the flood damage.
Base costs
![]() $ {q}_1,{q}_2,{q}_3 $
concern basic construction, occurring with probability one. Monster failure or poorly quantified costs concern costs
$ {q}_1,{q}_2,{q}_3 $
concern basic construction, occurring with probability one. Monster failure or poorly quantified costs concern costs
![]() $ {p}_1{q}_{p_1},{p}_2{q}_{p_2},{p}_3{q}_{p_3} $
with the probabilities including adverse monstrous climate-change effects. Each option leads to overall costs, assuming the probabilities to be independent, as follows:
$ {p}_1{q}_{p_1},{p}_2{q}_{p_2},{p}_3{q}_{p_3} $
with the probabilities including adverse monstrous climate-change effects. Each option leads to overall costs, assuming the probabilities to be independent, as follows:
The five flood-mitigation scenarios each mitigate the entire FEV responsible for flood damage of the simulated
![]() $ 1:50\mathrm{yrs} $
event, which is the designated design flood. Each scenario can be graphed as a square lake viewed from above with each option
$ 1:50\mathrm{yrs} $
event, which is the designated design flood. Each scenario can be graphed as a square lake viewed from above with each option
![]() $ (C1,B2, FP3 $
) portioning the square lake, cf. Figure 6, with costs per option overlaid. Any option involving the canal
$ (C1,B2, FP3 $
) portioning the square lake, cf. Figure 6, with costs per option overlaid. Any option involving the canal
![]() $ (C1 $
) can include additional storage against higher return-period or monster events beyond the target FEV emerging from the design flood, thus assimilating some monster events. Hitherto, the graphical cost-effectiveness tool has been used to inform decision-makers to make the available scenarios transparent, but no process has been developed to rationally and quantifiably choose between them. How do we value the monsters and fairies involved, in a just and science-based decision-making process, and choose the best one among these flood-mitigation scenarios?
$ (C1 $
) can include additional storage against higher return-period or monster events beyond the target FEV emerging from the design flood, thus assimilating some monster events. Hitherto, the graphical cost-effectiveness tool has been used to inform decision-makers to make the available scenarios transparent, but no process has been developed to rationally and quantifiably choose between them. How do we value the monsters and fairies involved, in a just and science-based decision-making process, and choose the best one among these flood-mitigation scenarios?

Figure 6. Square-lake cost-effectiveness graphs of five flood-mitigation scenarios to prevent High Beck surface flooding for the
![]() $ 1:50\mathrm{yr} $
design flood. These involve possible combinations of storage into canal (
$ 1:50\mathrm{yr} $
design flood. These involve possible combinations of storage into canal (
![]() $ C1 $
, purple), upstream bunds (
$ C1 $
, purple), upstream bunds (
![]() $ B2 $
, red) and/or downstream flood-plain storage (
$ B2 $
, red) and/or downstream flood-plain storage (
![]() $ FP3 $
, green). Base costs
$ FP3 $
, green). Base costs
![]() $ {q}_1,{q}_2,{q}_3 $
plus costs with uncertainty
$ {q}_1,{q}_2,{q}_3 $
plus costs with uncertainty
![]() $ {p}_1{q}_{p_1},{p}_2{q}_{p_2},{p}_3{q}_{p_3} $
have been superimposed using the double-sided arrows. Each square lake with a lateral depth of 1 m (out of the page) and side lengths of 98 m represents the FEV (
$ {p}_1{q}_{p_1},{p}_2{q}_{p_2},{p}_3{q}_{p_3} $
have been superimposed using the double-sided arrows. Each square lake with a lateral depth of 1 m (out of the page) and side lengths of 98 m represents the FEV (
![]() $ FEV\approx 9600{\mathrm{m}}^3\approx 98\mathrm{m}\times 98\mathrm{m}\times 1\mathrm{m} $
) to be reduced to zero by the combinations of mitigation measures. The canal measure
$ FEV\approx 9600{\mathrm{m}}^3\approx 98\mathrm{m}\times 98\mathrm{m}\times 1\mathrm{m} $
) to be reduced to zero by the combinations of mitigation measures. The canal measure
![]() $ C1 $
can provide extra mitigation (as indicated) by diverting less flood water to the downstream fields, thus reducing
$ C1 $
can provide extra mitigation (as indicated) by diverting less flood water to the downstream fields, thus reducing
![]() $ FP3 $
, and some to the canal
$ FP3 $
, and some to the canal
![]() $ C1 $
. In those partial cases, uncertain costs may be lower. Diverting flood waters into the canal does not affect the upstream measure
$ C1 $
. In those partial cases, uncertain costs may be lower. Diverting flood waters into the canal does not affect the upstream measure
![]() $ B2 $
.
$ B2 $
.
Note that in the square graphs presented here, we have left out the uncertainties in the FEV and the flood-mitigation-measure volumes (the rectangular areas in the graphs). The latter (mitigation) uncertainties can be represented to some extent by using the vertical axis as uncertainty axis, from least to most uncertainty, leading to triangular and quadrilateral instead of rectangular shapes, cf. Bokhove et al. (Reference Bokhove, Kelmanson, Kent, Piton and Tacnet2019) and Bokhove (Reference Bokhove2021).
The above is an example of how the strategies of monster assimilation and monster adaptation can be. The decision problem has been made structured and complexity has been reduced to an unavoidable minimum level. Yet a final step has to be made: decision-makers need to be informed in a comprehensible way, to support what decisions are deemed “good.” Otherwise, new monsters of uncertainty can grow. The question is also what characteristics define “good,” that is, decisions need to be rational, cost-effective/efficient, have minimum regret and maximum political support and so forth. Furthermore, decision-makers should be supported in Bayesian decision-making, which implies that uncertainties are explicitly incorporated in the decision-making process (Morgan and Henrion, Reference Morgan and Henrion1990).
The importance of what could characterize and qualify a “good decision” in FRM can be illustrated by considering what can cause suboptimal decisions. Addressing only one dimension of flood-mitigation problems, albeit rationally, may adversely affect other aspects in that the chosen solution taken:
-
(a) may lead to new problems (e.g., loss of ecological functions) (Auerswald et al., Reference Auerswald, Moyle, Seibert and Geist2019);
-
(b) has unintended long-term consequences (e.g., a dependence on higher flood-defense walls to contain river levels for 1-in-200 years protection in a narrow channel could lead to a false sense of security, especially as return periods reduce due to climate change, causing future overtopping or breaches) (Kates et al., Reference Kates, Colten, Laska and Leatherman2006; Di Baldassarre et al., Reference Di Baldassarre, Kooy, Kemerink and Brandimarte2013a, Reference Di Baldassarre, Viglione, Carr, Linda Kuil and Blöschl2013b; Gohari et al., Reference Gohari, Eslamian, Mirchi, Abedi-Koupaei, Bavani and Madani2013); and,
-
(c) has an uneven distribution of costs and benefits when other sectors and social groups are taken into account (e.g., if optimism bias about the extrapolation of NFM benefits were to cause reduced investment in other, more predictable, flood risk mitigations for vulnerable communities) (Savelli et al., Reference Savelli, Rusca, Cloke and Di Baldassarre2021).
Morgan and Henrion (Reference Morgan and Henrion1990) comprehensively discuss decision-taking criteria in their Section 3.4. In a nutshell, which does insufficient justice to their writing: they distinguish utility-based, rights-based, technology-based and hybrid criteria. In particular, maximization of a multi-attribute utility function would address the points above. Various relevant aspects are then brought together in one utility function, without assigning monetary values to relevant aspects. While that sounds simple, an apparent drawback can be that the as-such defined function often becomes complex and difficult to understand for the decision-makers. Transparency thereon and on the general decision-process can be achieved by defining the relevant decision-criteria and associated functionality at the beginning of the process with all relevant actors, including communication experts, in order to clearly define and accept the chosen criteria. Moreover, also in FRM, it is important to make the decision-process adaptive such that it can be revisited in the future, when new technology, observational data and information become available. Most organizations might find it difficult to adopt such adaptivity, but it should be adopted as long as the process is primarily geared to focus on improved decision-making and not on assigning blame for taking past wrong or suboptimal decisions. Finally, Morgan and Henrion (Reference Morgan and Henrion1990) discuss an “approved process” as decision criterion and declare that to be a widely used approach, in which a decision is considered acceptable when a specified set of procedures is followed. They point out that the language of decision analysis is inappropriate for such a social as opposed to analysis-based process.
A graphical cost-effectiveness tool was exemplified through a hypothetical study with five flood-mitigation scenarios. Each scenario had base construction costs and potentially additional costs associated with failures of uncertain nature, and some scenarios had a co-benefit. An outstanding question is how to construct a decision-tree in order to make the best decision under such uncertainties. While the square-lake cost-effectiveness graphics has proven to be beneficial to decision-makers, see Piton et al. (Reference Piton, Dupire, Arnaud, Mas, Marchal, Moncoulon, Curt and Tacnet2018a) and Piton et al. (Reference Piton, Pagano, Basile, Cokan and Lesjak2018b), a pressing question is how to visualize and explain decision-trees such these can be understood and applied by decision-makers.
This case study falls in the middle of our schematic of FRM-challenges displayed in Figure 1, as it is of intermediate complexity with estimates of the uncertainties involved. Intuitively, it seems obvious that the optimal scenario must include the canal-storage option since the canal offers extra buffer capacity beyond the target flood-excess volume FEV. However, when it turns out that the canal option becomes (nearly) impossible, it shifts the study to the right side of the schematic where FRM is poorly-structured: for example, when a combined-sewer overflow (CSO) pollutes the beck during intermediate rainfall and a short extra CSO-pipe along part of the beck and debris filter could prevent pollution flowing into the canal and lower pollution flow into the river, the issue can become that the public council is only responsible to deal with flooding, that the nonprofit “Trust” only maintains the canal and its ecological value, that private business “The Shire” is only responsible for the sewer system and that there is no legislation to enforce effective collaboration to solve the integral water-sewer management challenge described. A case of monster anesthesia?
The decision-making bodies on FRM can have highly different levels of expertise. In the Netherlands, for example, (fluvial and pluvial) FRM is channeled to a large extent through so-called waterboards or “Waterschappen,” which boards contain elected people who are exclusively focusing on decisions in water management. Perhaps in contrast, in the UK, FRM decisions span a range of organizations with differing responsibilities (Finlay and Bolton, Reference Finlay and Bolton2022), sometimes working independently, but often in partnership, and involving people with range of expertise and interests. Consequently, equipping decision-making bodies with adequate (visualization) tools to be engaged in a meaningful way with FRM will be a different task depending on the situation.
Discussion
In the present contribution, we have described the various guises of uncertainty monsters and possible coping strategies. If efficient decision-making in FRM is aimed for, then monster adaptation and monster assimilation are the preferred coping strategies. We argued that these strategies benefit from improving structure and reducing complexity of decision problems. Against this light, it is helpful to unpack the steps needed to effectively communicate uncertainties in FRM.
As exemplified by the cases above, a dominant aspect of FRM is the epistemic nature of uncertainty. That is, it deals with phenomena that we do not fully understand (yet) due to limited scientific knowledge or one being ignorant. Dealing effectively with epistemic uncertainty requires a deliberate risk communication strategy. In their framework, Van der Bles et al. (Reference Van der Bles, Van der Linden, Freeman, Mitchell, Galvao, Zaval and Spiegelhalter2019) stipulated that (1) what, (2) in what form, (3) to whom and (4) to what effect are all elements to be considered:
-
1. the object, source, level and magnitude of uncertainty;
-
2. how is the uncertainty described, in which format, and via which medium?
-
3. what kind of audience is involved, what is their relationship with the content of the communication and the communicator?
-
4. communication can have impact on the thinking (cognition), feeling (affect), trust and, importantly, decision-making.
However, neither maximized structure nor minimized complexity of decision problems nor prudent communication still do not guarantee that decision-makers take this information into account. Indeed, monster adaptation and assimilation imply careful consideration of information, referred to as the central route of information processing (Petty and Cacioppo, Reference Petty and Cacioppo1984). Decision-makers may not always be motivated or equipped to this. The attitudes of decision-makers can be changed via an alternative route, to which Petty and Cacioppo (Reference Petty and Cacioppo1984) refer as the peripheral route, characterized by informational cues, such as the number of arguments, the implied expertise of the communicator and so forth. These cues are not directly related to content of the message, but may still influence the decision-making process. Possibly, the involvement of decision-makers in monster adaptation or assimilation could be achieved by a more peripheral route of information processing along storylines, as Shepherd et al. (Reference Shepherd, Boyd, Calel, Chapman, Dessai, Dima-West, Fowler, James, Maraun, Martius, Senior, Sobel, Stainforth, Tett, Trenberth, van den Hurk, Watkins, Wilby and Zenghelis2018) proposed for representing uncertainty in physical aspects of climate change. The conventional approach to representing uncertainty in the physical aspects of climate change is probabilistic, based on ensembles of climate model simulations. However, in the face of deep uncertainties, the known limitations of this approach are becoming increasingly apparent. An alternative is thus emerging which may be called a “storyline” approach. Shepherd et al. (Reference Shepherd, Boyd, Calel, Chapman, Dessai, Dima-West, Fowler, James, Maraun, Martius, Senior, Sobel, Stainforth, Tett, Trenberth, van den Hurk, Watkins, Wilby and Zenghelis2018) defined storylines as “a physically self-consistent unfolding of past events, or of plausible future events or pathways. No a priori probability of the storyline is assessed; emphasis is placed instead on understanding the driving factors involved, and the plausibility of those factors.”
As discussed, structured and evidence-based approaches to communication will help our uncertainty monsters to be assimilated, provided that sufficient resources can be allocated to developing communication strategies that integrate with analyses such as those discussed in this paper. Where uncertainties can only be expressed as conditional on assumed future scenarios or narratives, the expert elicitation approach discussed earlier may be useful. Other, innovative approaches may emerge to aggregate information about uncertain future risks; for example, prediction markets have been proposed as an efficient mechanism to allocate funding for applied climate research (Roulston et al., Reference Roulston, Kaplan, Day and Kaivanto2022).
Open peer review
To view the open peer review materials for this article, please visit http://doi.org/10.1017/wat.2024.4.
Data availability statement
The csv-file, the Python code and Matlab code used in case C can be provided.
Acknowledgments
The authors are grateful to Deborah Oluwasanya (Cambridge University Press) for her enthusiastic support during the writing process. O.B. acknowledges fruitful discussions with and proofreading by Charles Taylor. P.M.P. kindly acknowledges the inspiration gained from the work by David Robert Jones. M.K. acknowledges Cees van Woerkum for sharing useful insights. Constructive and much-appreciated comments by one reviewer have led to several improvements. In particular, we use the reviewer’s comment as a starting point to discuss what could constitute good decision criteria.
Competing interest
The authors declare none.

























Comments
Dear Madam, Sir,
We are happy to submit our manuscript entitled “How to cope with uncertainty monsters in flood risk management”. We look forward to you decision on publication. We added an Impact Statement. The LaTeX template nor the submission system do mention an Impact Statement, however. We now submitted it as a PDF with “title page” as designation, we hope that this is to your convenience.
On behalf of all authors, Martin Knotters