Introduction
The spread of weighing devices in pre-literate Bronze Age Europe (Fig. 1) is generally viewed as the technological correlate of a cognitive shift towards the rational quantification of economic value (Pare Reference Pare, Fokkens and Harding2013; Peroni Reference Peroni2006; Rahmstorf Reference Rahmstorf, Morley and Renfrew2010; Renfrew Reference Renfrew, Papadopoulos and Urton2008). Whereas the origin of weight-systems is intimately correlated to the need of calculating incomes and expenditures, negotiating purchase-prices and assessing profit (Powell Reference Powell1977; Reference Powell1996), the very existence of a weight-based exchange presupposes ‘some generally accepted index of value together with a certain amount of haggling over price’ (Powell Reference Powell, Powell and Sack1979, 89), regardless of whether it is based on currency or barter.
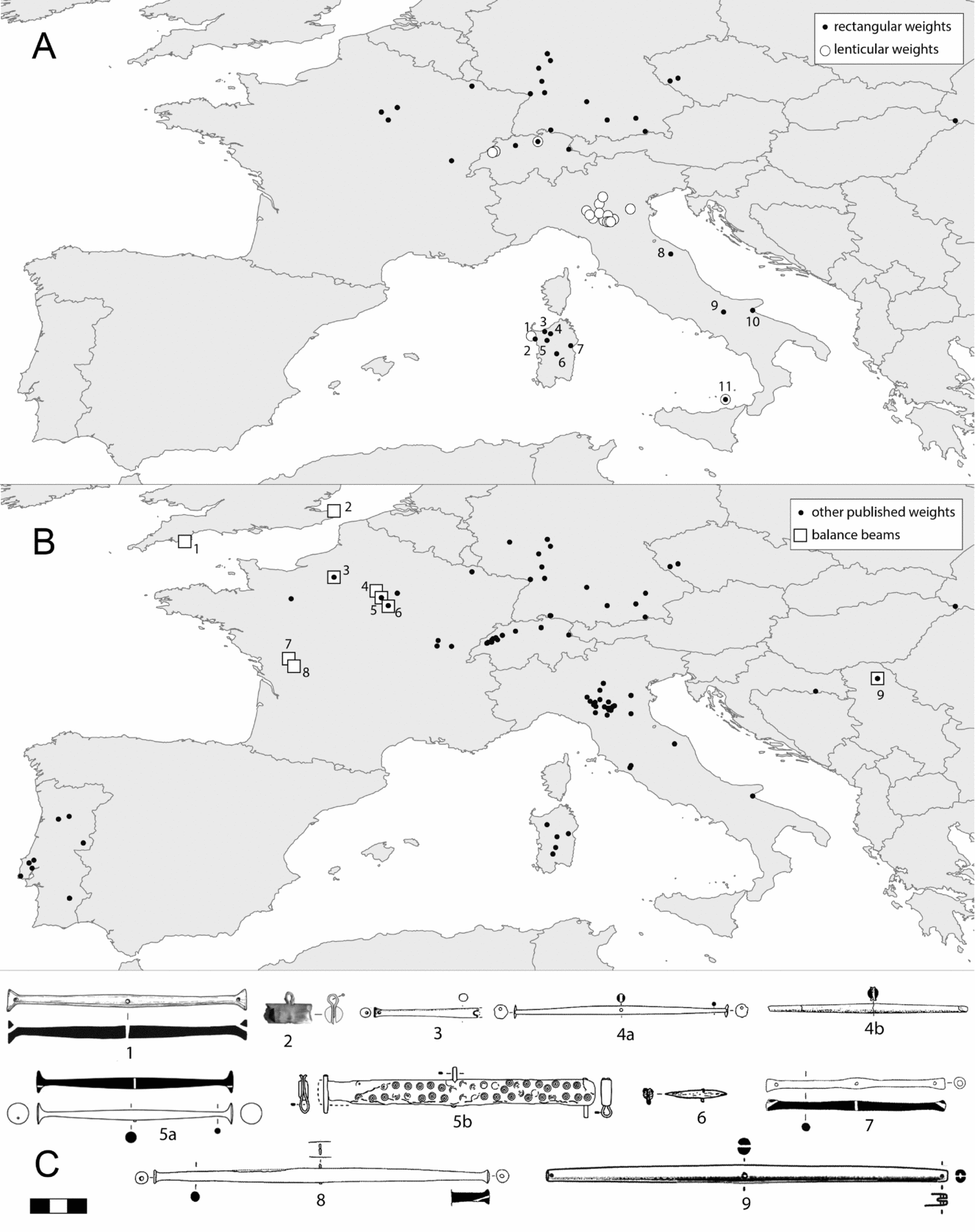
Figure 1. Distribution of weighing equipment in Bronze Age Europe. A: rectangular and lenticular weights. The numbers indicate the provenance of the unpublished material, previously unknown in archaeological literature. (1) Nuraghe Sant'Imbenia; (2) Nuraghe Palmavera; (3) Sa Tanca ‘e sa Idda; (4) Nuraghe Sa Mandra Manna; (5) Nuraghe Santu Antine; (6) Nuraghe Talei; (7) Serra Orrios; (8) Monte Croce-Guardia; (9) Oratino; (10) Coppa Nevigata; (11) Aeolian Islands. B: other published weights and balance beams. (1) Potterne (Lawson Reference Lawson2000, 40); (2) Cliffs End Farm (Schuster Reference Schuster, McKinley, Leivers, Schuster, Marshall, Barclay and Stoodley2014); (3) Fort Harrouard (Mohen & Bailloud Reference Mohen and Bailloud1987, pl. 85.8); (4) Marolles-sur-Seine (2 exemplars: Mordant & Mordant Reference Mordant and Mordant1970, fig. 31.16; Pare Reference Pare1999, fig. 22.1); (5) Migennes (2 exemplars: Roscio et al. Reference Roscio, Delor and Muller2011, fig. 2.35, 5.13); (6) Monéteau (Joly Reference Joly1965, fig. 21); (7) Agris, Grotte de Perrats (Peake et al. Reference Peake, Séguier and Gomez de Soto1999, fig. 1.2); (8) Vilhonneur, Grotte de la Cave Chaude (Peake et al. Reference Peake, Séguier and Gomez de Soto1999, fig. 1.3); (9) Bordjoš (Medović Reference Medović and Hänsel1995, fig. 4). C: bone and antler balance beams; the numbers correspond to the sites on the map.
However, weighing equipment and weight systems are still poorly understood in the framework of Bronze Age Europe, outside of Greece. Despite the widespread distribution of balance beams and weights, only a few specialist studies have been published so far on the subject, and a European metrology is still yet to be acknowledged as a proper research field. The main obstacle is represented by the lack of focus on methodologies that allow us to quantify confidence of the positive identification of potential balance weights in pre-literate societies. Starting from the most relevant literature in the field, this article outlines an extensive theoretical and methodological framework—based on testable hypotheses, reproducible experiments and clear expectations for experimental results—and tests it on a large sample collected from a vast territory, spanning southern Italy, central Europe and the Atlantic façade.
The research is grounded on the following assumption: the rise of a global network—seamlessly connecting Europe, the Mediterranean and the Near East in a constant flow of ideas, people and commodities (Harding Reference Harding, Fokkens and Harding2013; Vandkilde Reference Vandkilde2016)—implies the existence of widely shared means of quantifying, negotiating and communicating economic value. Since eastern Mediterranean trade was largely based on weight-based quantification, and part of pre-literate Europe was actively engaged in long-distance trade with the east, balance weights must have been used systematically in Bronze Age Europe as well, and especially in those regions where contacts with eastern civilizations are more frequent.
The actual distribution of weighing equipment shows that balance weights are well attested in Central Europe and Northern Italy—with minor concentrations in Portugal, Sardinia and eastern Europe (Fig. 1B)—but almost absent from southern Italy, where direct contacts with Aegean and eastern traders are most attested. In order to make a testable case for the base assumption, the research aimed at assessing whether balance weights are systematically attested in alleged trade hubs in southern Italy.
This article focuses on unpublished materials from the Aeolian Islands (Sicily). A European weight system is defined, largely independent from other Mediterranean units. The study leads to the identification of three types of potential balance weights, discusses their typological and metrological affinities with similar objects distributed in Italy, central Europe and the Mediterranean, addresses the relationship between European and Mediterranean weight systems and analyses their contextual associations. Being concentrated in levels dating to the first half of the second millennium bc, the Aeolian finds represent the earliest balance weights documented so far in Europe, west of Greece.
The broad culture-historical focus of this study roughly corresponds to the modern definition of Europe, with the exception of Greece. The absence of writing and centralized institutions sets the historical development of Bronze Age [hereafter BA] Europe slightly apart from the Aegean, as interpretive syntheses often remark (e.g. Fokkens & Harding Reference Fokkens, Harding, Fokkens and Harding2013; Harding Reference Harding2000, 4). This is even truer in the metrological field, where the lack of economic texts and inscribed weights urges a rethink of some aspects of the methodological framework.
The identification of balance weights: a multifaceted methodological problem
The confident identification of balance weights is the main obstacle for an independent metrology for pre-literate BA Europe. Unfortunately, balance weights are generally rather unremarkable objects, and thus they are seldom taken into account in prehistoric research (e.g. Kulakoğlu Reference Kulakoğlu, Çiğdem, Horowitz and Gilbert2017; Michailidou Reference Michailidou, Alberti, Ascalone and Peyronel2006; Petruso Reference Petruso1992; Pulak Reference Pulak1996; Rahmstorf Reference Rahmstorf, Alberti, Ascalone and Peyronel2006b). This may potentially have led to a large amount of evidence being ignored, misinterpreted as some kind of working tools, or even discarded during excavations.
Nevertheless, balance weights do possess recurrent shapes, and the construction of a knowledge for pre-literate BA Europe must start from a systematic typological appraisal. So far, specialist studies on pre-literate Europe have focused on specific regions, and typological connections between different areas have not been explored. This study is concerned, first, with the identification of widely spread formal types of artefacts that do not present clearly functional features—such as sharp edges, points, sockets, or tangs—but still present a recurrent, albeit simple, shape. This criterion, for example, allows the discard of many types of hammers, axes, or chisels, and also very simple tools, such as polishers and scrapers, that are often obtained from natural pebbles. There is indeed some ground to claim that, in some cases, natural pebbles were used as balance weights (Medović Reference Medović and Hänsel1995; Rahmstorf Reference Rahmstorf, Nessel, Heske and Brandherm2014a), but their identification is too problematic and it will not be addressed here. The typological selection provides a first appraisal of potential balance weights, to be tested through further criteria.
Use wear represents a problematic aspect of the identification process (Rahmstorf Reference Rahmstorf, Morley and Renfrew2010). Balance weights are tools, and since they were frequently manipulated one can expect, for instance, polishing from frequent use and accidental damage in the form of scratches and chipping. Technological traces deriving from the manufacture of the object itself must also be expected: this aspect is seldom taken into account in use-wear studies on polished-stone tools from the Bronze Age (e.g. Delgado Raack & Risch Reference Delgado Raack, Risch, Longo and Skakun2008; Iaia Reference Iaia2014) while it is a focal point of research for earlier periods (e.g. Breglia et al. Reference Breglia, Caricola and Larocca2016; Yerkes et al. Reference Yerkes, Khalaily and Barkai2012). This means, in turn, that several objects that are usually interpreted as ‘hard’ tools might actually be subject to different interpretations. Use wear from secondary use is often documented as well (e.g. Rahmstorf Reference Rahmstorf2006a). Residuals of external substances are also expected. At least one of the different modes of weighing documented in Near Eastern texts of the third and second millennia bc can be expected to cause extensive use wear and residual traces on balance weights: using a two-arm balance, when a quantity of raw material that is being assessed does not match the standard weight lying on the opposite pan, smaller balance weights can be added to the quantity being measured, until the scale reaches the point of equilibrium (Peyronel Reference Peyronel, Ascalone and Peyronel2011). Thus, for instance, the act of frequently laying a balance weight on top of or within a heap of metal ingots or scraps can produce scratches and residuals on its surface. To sum up, use wear may or may not be present on a single balance weight without substantially affecting its interpretation. The perspective shifts slightly, however, if we look at a whole category of potential balance weights. If use wear is not ‘systematically’ present on every object pertaining to a potential type of balance weights—i.e. if at least some of them do not show use wear—then one can conclude that ‘hard use’ is not a defining property of that type, thus opening the way to different interpretations.
Contexts represent a further criterion. Associations are a fundamental aspect, since they help define the context of use of potential balance weights. In the Aegean and in the Near East, occurrence in administrative quarters can support identification (e.g. Ascalone & Peyronel Reference Ascalone and Peyronel2006; Michailidou Reference Michailidou, Alberti, Ascalone and Peyronel2006; Rahmstorf Reference Rahmstorf, Morley and Renfrew2010; Schon Reference Schon2015). This criterion, however, is clearly useless for pre-literate BA Europe, where administrative institutions simply never existed. On the other hand, weighing equipment is already attested in the early third millennium bc in Greece and western Anatolia, before any evidence of centralized administrations (Rahmstorf Reference Rahmstorf and Molloy2016). It is also attested in private contexts in the ancient Near East already in the third millennium bc (e.g. Hafford Reference Hafford2005; Rahmstorf Reference Rahmstorf, Bieliński, Gawlikowski, Koliński, Ławecka, Sołtysiak and Wygnańska2014b), and in association with private book-keeping at least since the second millennium bc (Kulakoğlu Reference Kulakoğlu, Çiğdem, Horowitz and Gilbert2017). Balance weights are also well documented in private houses in Greece, during the second millennium bc (Petruso Reference Petruso1992, 35–6; Rahmstorf Reference Rahmstorf, Foster and Laffineur2003). Furthermore, the widespread presence of balance scales and weights in Continental Europe proves that the existence of central administrations is not even a requisite for the existence of weight systems. This urges focus on the ‘private’ sphere and on the material correlates of those economic activities that are most likely to rely on weight-based exchange. Based on both archaeological and textual evidence from the Near East and the Aegean, weight-based quantification is commonly associated, since the third millennium bc, with wool (e.g. Biga Reference Biga, Ascalone and Peyronel2011; Breniquet Reference Breniquet2008, 274–8; Liverani Reference Liverani1998, 52–8) and metals (e.g. Archi Reference Archi1988; Petruso Reference Petruso1992, 35–6; Powell Reference Powell1996; Rahmstorf Reference Rahmstorf, Bieliński, Gawlikowski, Koliński, Ławecka, Sołtysiak and Wygnańska2014b), while it is common opinion that weight systems came into use, in pre-literate Europe, as a consequence of the spread of metallurgy (e.g. Lenerz-de Wilde Reference Lenerz-de Wilde1995; Pare Reference Pare1999; Reference Pare, Fokkens and Harding2013; Peroni Reference Peroni and Hänsel1998; Primas Reference Primas1997; Renfrew Reference Renfrew, Papadopoulos and Urton2008). Therefore, the contextual analysis is aimed at assessing whether there are significant patterns of association between potential balance weights, textile production, metallurgy and metal trade.
Statistical analysis of the metrological properties of potential balance weights represents the last criterion. Other criteria provide circumstantial support, but the regularity of mass values is the single property that entirely subsumes the function of balance weights, and hence it is the only mandatory aspect for a positive identification. The identification of balance weights is a process of hypothesis testing, and as such, aims primarily at excluding unlikely alternatives. In this respect, the positive outcome of statistical tests on potential balance weights is the evidence that most effectively makes any other possible interpretation less likely. The metrological problem, however, is rather complex in itself, and will be treated separately.
The metrological problem: theoretical and methodological framework
Units of measurement between norm and practice
Units of measurement are pure theoretical concepts, whose function is to provide a frame of reference to comply with a norm. In the Bronze Age of the Near East and the Aegean, the wealth of cross-checked archaeological and textual evidence provides an ideal ground to explore how official, theoretically exact systems were organized and how they were reciprocally connected (Parise Reference Parise1971; Alberti et al. Reference Alberti, Ascalone, Parise, Peyronel, Alberti, Ascalone and Peyronel2006). However, any given physical unit becomes ‘exact’ only as soon as its equivalent value is formally fixed and written down in official accounts: everyday practice was—and still is (Ialongo & Vanzetti Reference Ialongo, Vanzetti, Biagetti and Lugli2016)—far from exact, and deviation from the norm was the norm itself (Chambon Reference Chambon2011). Approximate practice determined significant statistical dispersion in samples of balance weights, thus making excessive reliance on supposedly exact units often misleading. However, several studies have shown that advanced statistical methods yield great potential in the empirical evaluation of weight systems, even without relying on exact units as ultimate principles (e.g. Hafford Reference Hafford2005; Reference Hafford2012; Ialongo et al. Reference Ialongo, Vacca and Peyronel2018a; Pakkanen Reference Pakkanen and Brysbaert2011; Petruso Reference Petruso1992; Rahmstorf Reference Rahmstorf, Morley and Renfrew2010).
This study proceeds under the assumption that local weight systems, regardless of theoretical units, tend to normalize within large-scale trade networks (Ialongo et al. Reference Ialongo, Vacca and Peyronel2018a). The existence of standard weight systems implies compliance with a norm, but a self-regulated network based on customary commercial relationships can enforce such a norm effectively, even in the absence of centralized regulatory authorities (Chambon Reference Chambon, Alberti, Ascalone and Peyronel2006; Ialongo et al. Reference Ialongo, Vacca, Vanzetti, Brandherm, Heymans and Hofmann2018b; Rahmstorf Reference Rahmstorf, Morley and Renfrew2010). The success of a large-scale network does not even require complying with a single weight system: the existence of different units in the Aegean, Anatolia, the Levant and Mesopotamia in the Bronze Age, for example, did not hamper trade between these regions in any noticeable way.
Comparative metrology and ‘imported’ units: the pitfalls of an ill-posed problem
Research on balance weights of pre-literate Bronze Age Europe is traditionally based on the quest for exact units (e.g. Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bernabò Brea, Cardarelli and Cremaschi1997; Lo Schiavo Reference Lo Schiavo, Alberti, Ascalone and Peyronel2006; Pare Reference Pare1999; Vilaça Reference Vilaça, Aubet Semmler and Sureda Torres2013), firmly rooted in the assumption that European systems must be based on (or entirely derived from) Aegean or Near Eastern units. The analytical praxis of comparing different systems, under the assumption that they are structurally connected, is defined as ‘comparative metrology’ (Chambon Reference Chambon2011, 28–38; Powell Reference Powell, Powell and Sack1979). Hence, every supposed ‘unit’ resulting from the study of balance weights is equated to the most similar one among those that have been already suggested for eastern systems. Already in the early 1900s (Viedebantt Reference Viedebantt1917; Weissbach Reference Weissbach1916), sharp critiques of the ‘comparative approach’ were published, which came to the conclusion that ‘comparative metrology could be of value only after the specialized metrologies had created a more secure basis for comparison’ (Powell Reference Powell, Powell and Sack1979, 76). Moreover, this approach overlooks the massive trade network that connected pre-literate Europe in the Bronze Age (e.g. Earle et al. Reference Earle, Ling, Uhnèr, Stos-Gale and Melheim2015; Harding Reference Harding, Fokkens and Harding2013; Pare Reference Pare, Fokkens and Harding2013; Renfrew Reference Renfrew, Papadopoulos and Urton2008) that may have prompted the formation of independent systems of measurement.
Different Mediterranean units have been ‘identified’ for potential balance weights in central and western Europe, while no local system was ever acknowledged: an ‘Ugaritic’ unit in Portugal (9.3–9.4 g: Vilaça Reference Vilaça, Aubet Semmler and Sureda Torres2013), a ‘Microasiatic’ unit in Sardinia (11.75 g: Lo Schiavo Reference Lo Schiavo, Alberti, Ascalone and Peyronel2006) and an ‘Aegean’ unit between northern Italy and central Europe (c. 6.1–6.7 g: Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bellintani, Corti and Giordani2001; Feth Reference Feth, Nessel, Heske and Brandherm2014; Pare Reference Pare1999). However, none of these studies makes use of statistical techniques that allow testing the significance of their samples.
A further problem is overconfident reliance on the identification of foreign units whose definition is often still debated. The very existence of the alleged Aegean unit of c. 6.1–6.7 g (Zaccagnini Reference Zaccagnini1999–Reference Zaccagnini2001), for example, is highly uncertain. Such a light unit is derived from a heavier one of c. 58–65 g; while the heavy unit is strongly supported by both inscribed weights and statistical tests (Petruso Reference Petruso1992), there is no clear support for a light unit of c. 1/10 of its value (Hafford Reference Hafford2012).
Finally, excessive focus on exactitude determines a lack of attention towards issues of approximation and statistical dispersion (Hafford Reference Hafford2012; Ialongo et al. Reference Ialongo, Vacca, Vanzetti, Brandherm, Heymans and Hofmann2018b; Lo Schiavo Reference Lo Schiavo, Lo Schiavo, Muhly, Maddin and Giumlia-Mair2009; Petruso Reference Petruso1992, 4–7). When we try to identify a unit, we must always bear in mind that that unit simply represents a theoretical ‘mode’ of a statistical dispersion that normally falls within a range of ±5 per cent (sometimes even more: Hafford Reference Hafford2012) in terms of relative standard deviation (i.e. no less than ±10 per cent, if we consider a 2σ distribution). It can even happen that two similar, but distinct, theoretical units are so close that the respective statistical dispersions overlap to a point where they are almost impossible to discern (Hafford Reference Hafford2012): this is the case, for example, of the ‘Syrian’ (7.8 g) and the ‘Mesopotamian’ (8.4 g) shekels, whose respective error distributions significantly overlap at a standard deviation of ±5 per cent (Ialongo et al. Reference Ialongo, Vacca and Peyronel2018a). All in all, this means that, when we think we recognize a close similarity between two supposed units, we might be looking, in fact, at two distinct systems that just happen to be similar enough to be confused. The existence of a weight-system indeed implies the existence of units of measurement, but the absence of texts and quantity marks urges postponement of the quest for exact units until a more solid metrological framework is available for pre-literate BA Europe.
Methodology
Frequency Distribution Analysis (FDA) and Cosine Quantogram Analysis (CQA) are the most used statistical methods. The aim of FDA is to identify significant clusters of weight-values; once they are located (if they are present at all) the analysis follows up with checking whether the mode of each cluster may correspond to approximate multiples of a same basic value. CQA is a more advanced method, introduced in contemporary weight metrology by Petruso (Reference Petruso1992). In physics, a quantum is the minimal amount of any physical entity employed in an interaction; in weight metrology, the same term defines the amount of mass that ‘fits’ the largest possible amount of measurements in a sample. CQA was devised by Kendall (Reference Kendall1974) to test whether an observed measurement X is an integer multiple of a ‘quantum’ q plus a small error component ε. X is divided for q and the remainder (ε) is tested. Positive results occur when ε is close to either 0 or q, i.e. when X is (close to) an integer multiple of q, where N is the sample size:
 $$\begin{equation*}
\phi \left( q \right) = \ \sqrt {2/N} \ \mathop \sum \limits_{i = 1}^n \ {\rm{cos}}\left( {\frac{{2\pi {\varepsilon _i}}}{q}} \right)
\end{equation*}$$
$$\begin{equation*}
\phi \left( q \right) = \ \sqrt {2/N} \ \mathop \sum \limits_{i = 1}^n \ {\rm{cos}}\left( {\frac{{2\pi {\varepsilon _i}}}{q}} \right)
\end{equation*}$$
Plotted in a graph, the results show high positive peaks where a quantum gives a high positive value for ϕ(q). The advantage of CQA over FDA mainly consists in the fact that the former provides an estimation of likely quanta, while in the latter the quanta must be calculated separately, in the absence of a strict framework. A spreadsheet for the calculation of CQA is appended to this paper online as downloadable supplementary material.
CQA is affected by several potential sources of bias (e.g. small sample size, inaccuracy of measurement, coexistence of different unit systems) and its results should be tested for statistical significance (Kendall Reference Kendall1974; Pakkanen Reference Pakkanen and Brysbaert2011). Monte Carlo simulations were executed (based on Kendall Reference Kendall1974) under the null-hypothesis that the sample of potential balance weights is not ‘quantally configured’, i.e. that the observed probability distribution is due to chance. The samples were randomized by adding a random fraction of ±15 per cent to each measurement. The simulation was applied 100 times and each generated dataset was analysed through CQA. The aim of the test is to observe whether a random dataset with similar distribution can produce values for ϕ(q) equal to or higher than those obtained for the real dataset, for the same range of quanta. If randomized samples can consistently score higher values than the real sample, it means that we cannot exclude that the probability distribution of the latter is simply due to chance. Since the sample of this study was collected from a very wide area, from different publications with different levels of weighing accuracy, the alpha level is set to 0.05, i.e. equal or higher results must not occur in more than 5 per cent of the iterations in order for the null-hypothesis to be rejected.
Expectations
CQA is not expected to show a single ‘peak’, but a series of peaks that are related to a consistent sequence of multiples and fractions. When this happens, and when at least one of the peaks is statistically significant, then the sample is said to be ‘quantally configured’, i.e. the quanta indicated by the analysis are good descriptors of the variability of the sample (Kendall Reference Kendall1974).
It is important to clarify the real capabilities of CQA: in the absence of texts and inscribed weights, it will never be possible to identify which one of the peaks is the actual unit. For a perfectly quantal sample (i.e. a sample made entirely of multiples of the same exact number), the CQA will produce peaks of the same height for every single logical fraction or multiple of the unit itself. The example in Figure 2 shows the results for a perfectly quantal set of observations, corresponding to the nominal weights written on the labels of packaged goods in modern supermarkets in Italy (Ialongo & Vanzetti Reference Ialongo, Vanzetti, Biagetti and Lugli2016). The Quantogram shows a series of equally high peaks at the values of 1 g, 2 g, 2.5 g, 5 g, 10 g, 12.5 g, 25 g and 50 g: if we did not know that the unit of the Decimal System is ‘1’, we would never be able to figure it out, not even with a perfectly quantal dataset. ‘The unit’ is merely a theoretical concept, and cannot be translated into practice without knowing the underlying normative system.
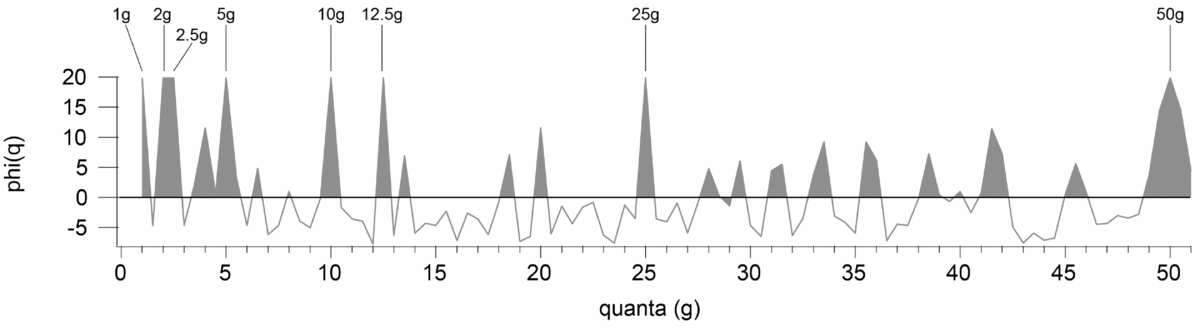
Figure 2. Quantogram of a perfectly quantal sample: weight values written on the labels of packaged goods in Italian supermarkets. (Ialongo & Vanzetti Reference Ialongo, Vanzetti, Biagetti and Lugli2016.)
Similar cases are documented in archaeological contexts. For instance, the balance weights of the city of Larsa (southern Mesopotamia, second millennium bc) consistently produce high peaks around 5.6 g, corresponding to two-thirds of the ‘Mesopotamian unit’ of 8.4 g (Ascalone & Peyronel Reference Ascalone and Peyronel2006, 451–64; Ialongo et al. Reference Ialongo, Vacca and Peyronel2018a). Moreover, the inscribed weights from Ayia Irini (Crete) clearly indicate a unit between c. 58 and 65 g (Petruso Reference Petruso1992, 61); however, while the CQA shows very good ‘peaks’ for the complete array of logical fractions of the unit, it does not indicate any positive result for the unit itself (see further, Fig. 10). In both cases, a normative unit does indeed exist, but, if we could not reconstruct its actual value through texts and inscribed weights, we could conclude—erroneously—that ‘the unit’ is the value suggested by the statistical analysis.
From a statistical point of view, therefore, a significant result for a series of logical multiples is enough to validate the quantal hypothesis, whereas its historical interpretation must still be evaluated against other sources of evidence.
3D reconstruction of chipped weights
The chipped objects that were documented directly during this research were subject to 3D scanning and digitally reconstructed (Fig. 3). The volume before and after the reconstruction was measured and the original mass was calculated based on density. Density (d) is a function of volume (v) and mass (m) (d = m/v), and the reconstruction is based on the assumption that, whatever the material employed, every object has an approximately uniform density. Hence, the reconstructed mass (m1) is obtained from a reconstructed volume (v1), given its density (m1 = d* v1). Obviously, this method is only valid for those objects whose original shape can be easily reconstructed (like the example in Figure 3).

Figure 3. 3D reconstruction of chipped weights.
Weighing equipment in Bronze Age Europe: state of the art
Long after an early appraisal of the problem (Forrer Reference Forrer1906), research on weighing equipment in pre-literate Bronze Age Europe has seen substantial advancements only in the last 20 years or so (Fig. 1B). A study of stone weights in Northern Italy (Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bernabò Brea, Cardarelli and Cremaschi1997; Reference Cardarelli, Pacciarelli, Pallante, Bellintani, Corti and Giordani2001; Reference Cardarelli, Pacciarelli, Pallante, De Sena and Dessales2004) was shortly followed by the identification of a class of rectangular weights, widely attested in central Europe (Pare Reference Pare1999). Surveys of Portuguese (Vilaça Reference Vilaça2003, Reference Vilaça, Aubet Semmler and Sureda Torres2013), Sardinian (Ialongo Reference Ialongo2011; Lo Schiavo Reference Lo Schiavo, Alberti, Ascalone and Peyronel2006) and Alpine (Feth Reference Feth, Nessel, Heske and Brandherm2014) contexts led to the identification of several types of potential balance weights. Apart from a few objects from northern Italy, dating to around 1500 bc (Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bellintani, Corti and Giordani2001), the materials date to no earlier than 1400–1350 bc. Solid evidence for the existence of weight systems is also provided by the widespread attestation of balance scales. At least 11 bone/antler balance beams are attested in the Late Bronze Age (Fig. 1B–C), and several other doubtful exemplars (Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bellintani, Corti and Giordani2001; Rahmstorf Reference Rahmstorf, Nessel, Heske and Brandherm2014a). The European evidence is rather exceptional: in the Near East, for example, only one exemplar of a balance beam is known for the whole Bronze Age (Genz Reference Genz2011; Peyronel Reference Peyronel, Ascalone and Peyronel2011), despite thousands of balance weights being attested in dozens of different sites. Balance scales are somewhat more common in Greece and Cyprus, balance pans being usually the only part preserved (Pare Reference Pare1999). This suggests that many more balances must have existed that were mainly realized in wood, as is documented, for example, in Sumerian texts of the third millennium bc (Peyronel Reference Peyronel, Ascalone and Peyronel2011).
The Aeolian setting in the Bronze Age
The Aeolian Islands are a small volcanic archipelago, located off the northeastern coast of Sicily. Between the 1950s and 1980s, the archipelago was the object of an extraordinary research programme, leading to the extensive excavation of several settlements and cemeteries, spanning the entire arc of the Bronze Age (c. 2300–950 bc, in Italian chronology) (Bernabò Brea & Cavalier Reference Bernabò Brea and Cavalier1968; Reference Bernabò Brea and Cavalier1980; Reference Bernabò Brea and Cavalier1991) (Fig. 4).

Figure 4. Aeolian Islands, distribution of sites with potential balance weights. (1) Filicudi–Capo Graziano; (2) Salina–Portella; (3) Lipari–Acropolis.
For the entire duration of the BA, the Aeolian Islands are fully integrated in Mediterranean networks. Imported Aegean vessels are attested from at least the Capo Graziano 2 phase (c. 1700–1500 bc) until the Ausonio II phase (c. 1200–950 bc) (Jones et al. Reference Jones, Levi and Bettelli2014, 50–54). Cypriot materials occur in layers dating to c. 1500–1350 bc (Martinelli Reference Martinelli2005, 255–60). Proofs of external contacts also include metal and amber, distributed throughout the entire sequence, and the exceptional recovery of a tin ingot (c. 1500–1350 bc: Bettelli & Cardarelli Reference Bettelli, Cardarelli and Martinelli2010). Finally, impasto vessels of Aeolian production, dating to the first half of the second millennium bc, were recovered on the island of Vivara (Naples), some 260 km to the north (Cazzella et al. Reference Cazzella, Levi and Williams1997).
Rectangular weights
Typology
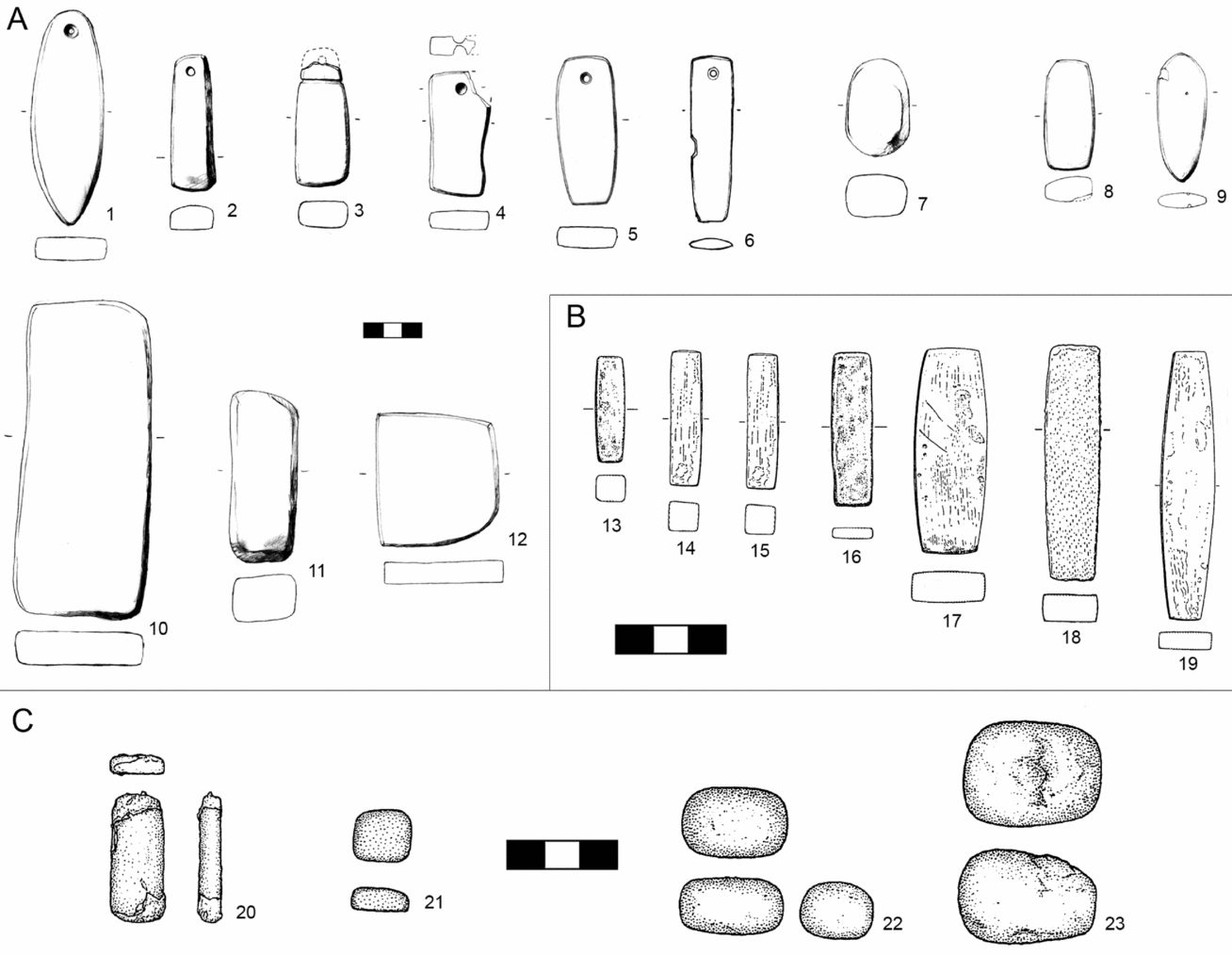
All the stone objects from Bernabò Brea's excavations (currently preserved in the Bernabò Brea Museum in Lipari) were sorted through, with the exception of flint and obsidian tools. The objects identified as potential balance weights are polished, stone parallelepipeds (Fig. 5), ranging between 6.66 g and 469.41 g.

Figure 5. Potential balance weights from the Aeolian Islands. A: rectangular weights; B: lenticular weights; C: sphendonoid weight.
While these objects pertain to a formal type that is commonly classified as ‘whetstone’, they show no clear traces of use wear; furthermore, most of them are realized in soft stones such as schist, limestone, steatite and pyroclastic material, unsuitable for hard use. The objects were not subject to a microscopic analysis by a specialist. However, detailed 3D models, possessing a level of detail of the order of c. 1/10 mm, aided observation. None of the objects shows dense patterns of parallel or cross-cutting lines compatible with sharpening, and most of them possess uniform textures that do not show any localized smooth patches, grooves from rubbing, or percussion traces.
Twenty objects were identified in total: 16 are plain parallelepipeds, with straight or convex sides (Fig. 5.1–13, 16–18). Three objects present a hole towards the top end (Fig. 5.14, 19–20). The heaviest one (Fig. 5.15) presents a rounded end and a circular hollow, possibly an aborted perforation or some sort of identification mark. Four more objects of this type are described in the publication (Bernabò Brea & Cavalier Reference Bernabò Brea and Cavalier1980), but could not be found in the storerooms.
Rectangular weights are attested throughout the entire BA sequence, in three different settlements: Lipari-Acropolis, Salina-Portella and Filicudi-Capo Graziano (Fig. 4). Fifteen exemplars come from layers dated to the ‘Capo Graziano’ phase (c. 2300–1500 bc), two from the ‘Milazzese’ phase (c. 1500–1350 bc) and three from the ‘Ausonio II’ phase (c. 1200–950 bc).
The majority of the finds belongs to the Capo Graziano phase, the earliest of the Aeolian BA sequence. The term ‘Capo Graziano’ (from the eponymous village on the island of Filicudi) identifies ceramic assemblages attested in northeast Sicily, between the Early Bronze Age (c. 2300–1700 bc) and the beginning of the Middle Bronze Age (c. 1700–1500 bc). Imported Aegean pottery is present in many Capo Graziano contexts (Jones et al. Reference Jones, Levi and Bettelli2014, 50–54). Typological considerations suggest that the village on the ‘Acropolis’ of Lipari mostly pertains to the sub-phase Capo Graziano 2 (Bernabò Brea & Cavalier Reference Bernabò Brea and Cavalier1980, 217–58), dating between c. 1730–1500 cal. bc (Alberti Reference Alberti2013; Martinelli et al. Reference Martinelli, Fiorentino and Prosdocimi2010). Twelve out of 20 rectangular weights come from the Capo Graziano layers on the Acropolis, suggesting a notable concentration of the evidence in sub-phase Capo Graziano 2. While it cannot be ruled out that some of the objects pertain to the earlier sub-phase, the evidence from the Acropolis provides a solid terminus ante quem at c. 1500 cal. bc: this makes the Aeolian weights the earliest known in Europe so far, outside of Greece.
The type is also well attested in peninsular Italy and Sardinia (Fig. 6A). All the objects come from Bronze Age settlements, the overall chronology spanning between c. 1500 and 725 bc. The materials from Coppa Nevigata (e.g. Cazzella et al. Reference Cazzella, Moscoloni and Recchia2012) and Monte Croce-Guardia (e.g. Cardarelli et al. in press) include several types of potential balance weights that are currently under study, and only the objects pertaining to the rectangular type are considered in this article. The Italian materials are very similar to rectangular weights widespread in central Europe in the LBA—mainly made of bronze, but with a few exemplars in stone—already identified by Pare (Reference Pare1999) (Fig. 6B). In the Late Bronze Age necropolis of Migennes, in France, two balance beams were found in the same grave, together with sets of rectangular weights (Roscio et al. Reference Roscio, Delor and Muller2011). In the eastern Mediterranean, this shape is not very common: a few stone weights from the shipwrecks of Uluburun and Cape Gelydonia can be vaguely compared (Fig. 6C) (Pulak Reference Pulak1996), and a single bronze weight from Uluburun is very similar (Fig. 6.20). The eastern Mediterranean evidence is substantially later than the Aeolian weights, and cannot be used to prove a dependency of western weights on eastern models; besides, it cannot be excluded that some of the rectangular weights in the Anatolian shipwrecks are of western origin.
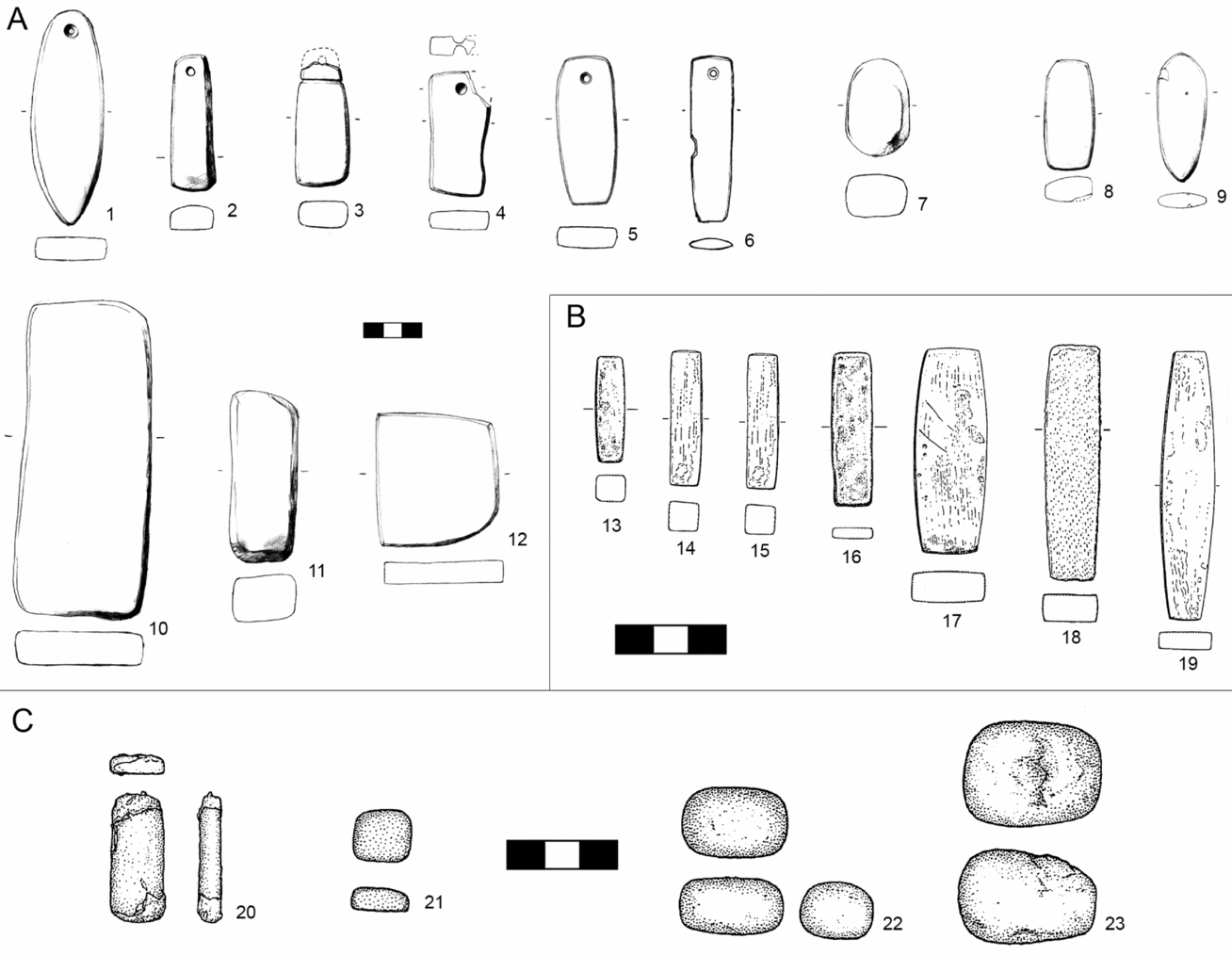
Figure 6. Potential rectangular weights. A: unpublished materials from Peninsular Italy and Sardinia; B: central Europe (from Pare Reference Pare1999); C: (20–21) Uluburun (from Pulak Reference Pulak1996); (22–23) Cape Gelydonia (from Pulak Reference Pulak1996).
Metrology
The sample of rectangular weights includes all the unpublished objects pertaining to this class attested in the Aeolian Islands (n = 16), Sardinia (n = 7) and peninsular Italy (n = 6), 23 objects identified by Pare (Reference Pare1999) in central Europe, six rectangular weights from the burial of Migennes and five objects from the site of Zug-Sumpf, in Switzerland (Bolliger Schreyer et al. Reference Bolliger Schreyer, Maise, Rast-Eicher, Ruckstuhl and Speck2004, Taf. 228). The sample comprises 63 complete or reconstructed items in total, ranging between 0.3 g and 469.41 g. The range of mass values is too wide for a single analysis to be accurate: therefore, the sample was split into two smaller, partially overlapping datasets of 1.5–20 g and 15–470 g; the smallest objects (three in total: 0.30 g, 0.39 g, 1.06 g) were not considered, since the very small size can produce an excessive measurement error.
Frequency Distribution Analysis (FDA) shows that the sample forms neat clusters around 3–3.5 g, 6.5–7 g, 13 g, 20 g, 40 g, 50 g, 60 g and 80 g (Fig. 7A). Both datasets were analysed through CQA, targeting 1000 quanta between 1 g and 4 g and between 4 g and 24 g, respectively (Fig. 7B). The significance test rejects the null hypothesis: the quanta at 1.1 g, 1.65 g and 19.54 g are statistically significant, the latter being beyond the 1 per cent significance threshold (alpha = 4.56), i.e. there is less than a 1 per cent chance that a random dataset with the same distribution can produce a quantum with ϕ(q)> = 4.56 in the same range. The analyses show five further peaks around 3.3 g, 4.08 g, 5.16 g, 6.34 g and 10.24 g. The complete array of values forms a perfectly logical series of multiples and fractions, as is expected from quantally configured datasets (Kendall Reference Kendall1974; Pakkanen Reference Pakkanen and Brysbaert2011). By taking the quantum at 19.54 g as reference (for no other reason than being ‘the highest’), we obtain a sequence of fractions corresponding to 1/18, 1/12, 1/6, 1/5, 1/4, 1/3 and 1/2.
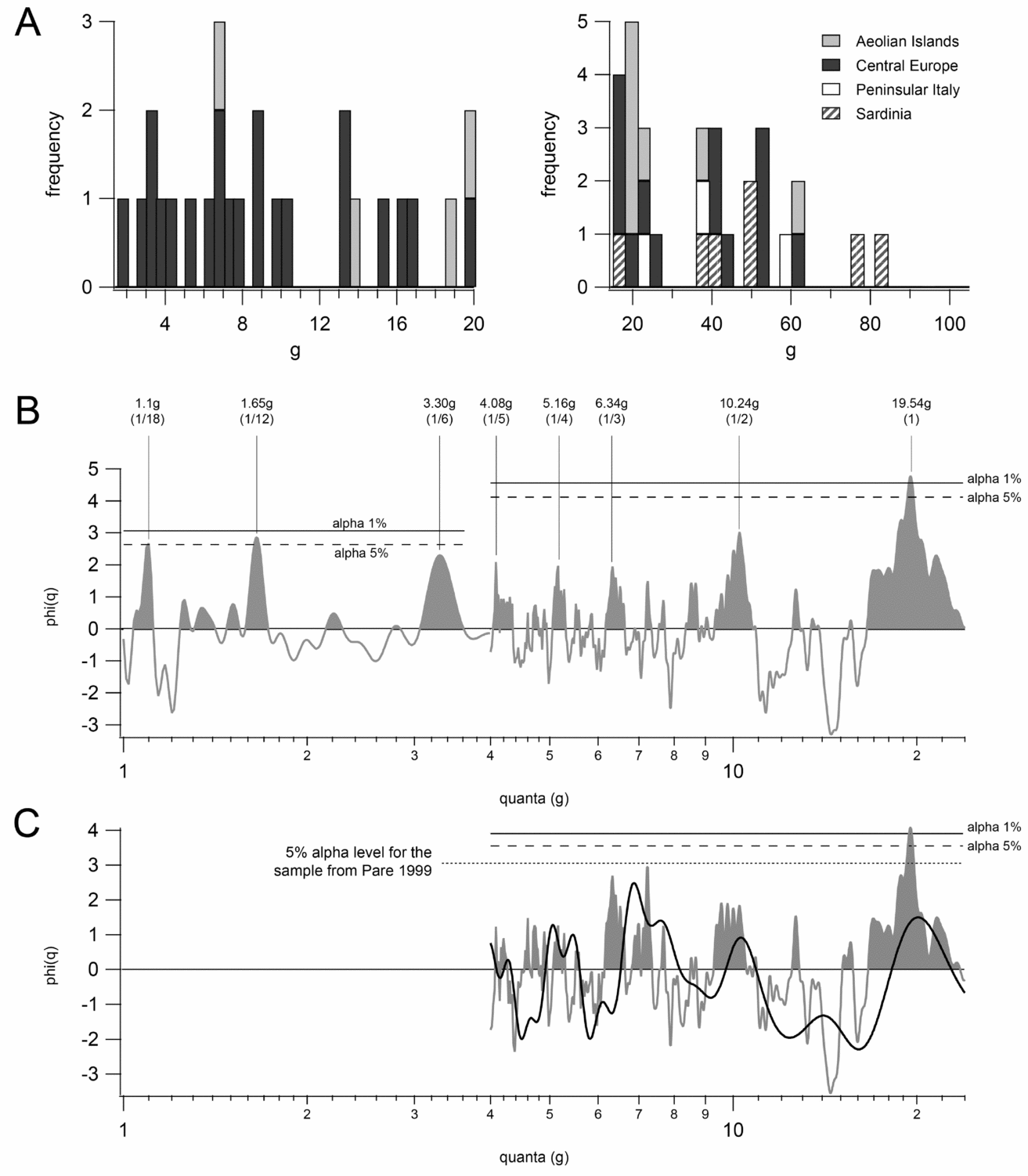
Figure 7. Statistical analysis of potential rectangular weights. A: Frequency Distribution Analysis. B: Cosine Quantogram Analysis of the total sample of potential rectangular weights; the fractions refer to the highest peak at 19.54 g. C: Comparison between the Italian sample (grey area) and the sample collected in Pare (Reference Pare1999) (black line). The CQA is displayed using a logarithmic scale, since the concentration of the peaks in the lower range would make the graph otherwise unreadable.
The small sample of rectangular weights from Central Europe was analysed by Pare through CQA (1999); the results are very similar to those obtained in the present study. The comparison between the quantograms of the Italian and of the central European samples shows that the peaks are located approximately in the same position, coinciding, in turn, with the peaks of the total sample (Fig. 7C). Pare identifies the possible unit of the central European weights in the peak between 6 g and 7 g, proposing to connect it to a hypothetical ‘Aegean’ unit of slightly more than 6 g. However, the current analyses suggest that such a peak can as well be a by-product of a series based on either c. 5 g, 10 g or 20 g (or any multiple of these numbers), of which the value between 6 g and 7 g would represent just a logical fraction. Moreover, the tests clearly show that the Italian sample is significant even if considered separately, while the central European one is not. The comparison between the two samples demonstrates that the two series are perfectly compatible, but also that the relative height of the peaks in the sample from central Europe is not significant.
Lenticular weights
Typology
The type includes lenticular objects, always made of stone, with an annular groove or a flattened surface along the diameter. Four of these objects were identified in the Aeolian Islands (Fig. 5B): one from the Acropolis of Lipari (Ausonio II phase, c. 1200–950 bc) and three from Salina-Portella (Milazzese phase, c. 1500–1350 bc). None of them shows clear traces of use wear. These objects are mainly realized in sandstone, but a few exemplars are made of limestone, marble and porphyry (Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bellintani, Corti and Giordani2001), which, together with the absence of systematic use wear, suggests that the type was not meant to be regularly used in working activities.
The type has been already identified as a potential class of balance weights in northern Italy, with a chronology of c. 1500–1150 bc (Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bernabò Brea, Cardarelli and Cremaschi1997; Reference Cardarelli, Pacciarelli, Pallante, Bellintani, Corti and Giordani2001; Reference Cardarelli, Pacciarelli, Pallante, De Sena and Dessales2004) (Fig. 8.2–3). At least one exemplar is documented in Sardinia, at the coastal site of Sant'Imbenia (e.g. Rendeli Reference Rendeli2012), from a context of the mid eighth century bc (Fig. 8.1). These objects are also widely attested in continental Europe (known as ‘Kanneluren-‘ or ‘Rillensteine’: Horst Reference Horst1981) (Fig. 8.4–5), although their interpretation as balance weights was never discussed. The variant with the flattened diameter is also similar to a type of balance weight attested in the eastern Mediterranean (Fig. 8.6–7).

Figure 8. A: Potential lenticular weights. (1) Nuraghe Sant'Imbenia; (2–3) northern Italy (from Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bellintani, Corti and Giordani2001); (4–5) Alpine pile-dwellings (Leuvrey Reference Leuvrey1999); (6–7) Uluburun (from Pulak Reference Pulak1996). B: sphendonoid weights (from Pulak Reference Pulak1996). (8) Uluburun; (9) Cape Gelydonia.
Metrology
The sample of lenticular weights includes 65 items in total, ranging between 275.43 g and 1273 g: two objects from the Aeolian Islands, 38 from Northern Italy, 20 from pile-dwelling settlements in Switzerland (Bolliger Schreyer et al. Reference Bolliger Schreyer, Maise, Rast-Eicher, Ruckstuhl and Speck2004, Taf. 223–225; Leuvrey Reference Leuvrey1999, 79–81), and one, unpublished, from Nuraghe Sant'Imbenia in Sardinia (Fig. 8.1), for an overall chronology between c. 1500 and 750 bc. Two outliers were removed before the analyses, in order to maintain the sample at a homogeneous scale: one weight from the Aeolian Islands (2,929 g), and one from Northern Italy (41 g). Finally, a chipped object from the Aeolian Islands was not considered, since it was not possible to obtain a 3D scan.
FDA indicates that lenticular weights cluster around c. 440 g, 550 g, 660 g, 850 g and 1,250 g (Fig. 9). The CQA shows three statistically significant peaks at 27.5 g, 107.5 g and c. 440 g (Fig. 10). The three peaks are part of a logical sequence of multiples: 27.5 g is almost exactly a quarter of 107.5 g, and exactly one-sixteenth of 440 g. Cardarelli et al. propose a unit of c. 54 g for the lenticular weights, which is perfectly compatible with the CQA results (54≈27.5×2≈107.6/2≈440/8). All these numbers are equally good candidates to serve as a unit of measurement.

Figure 9. Frequency Distribution Analysis of potential lenticular weights.
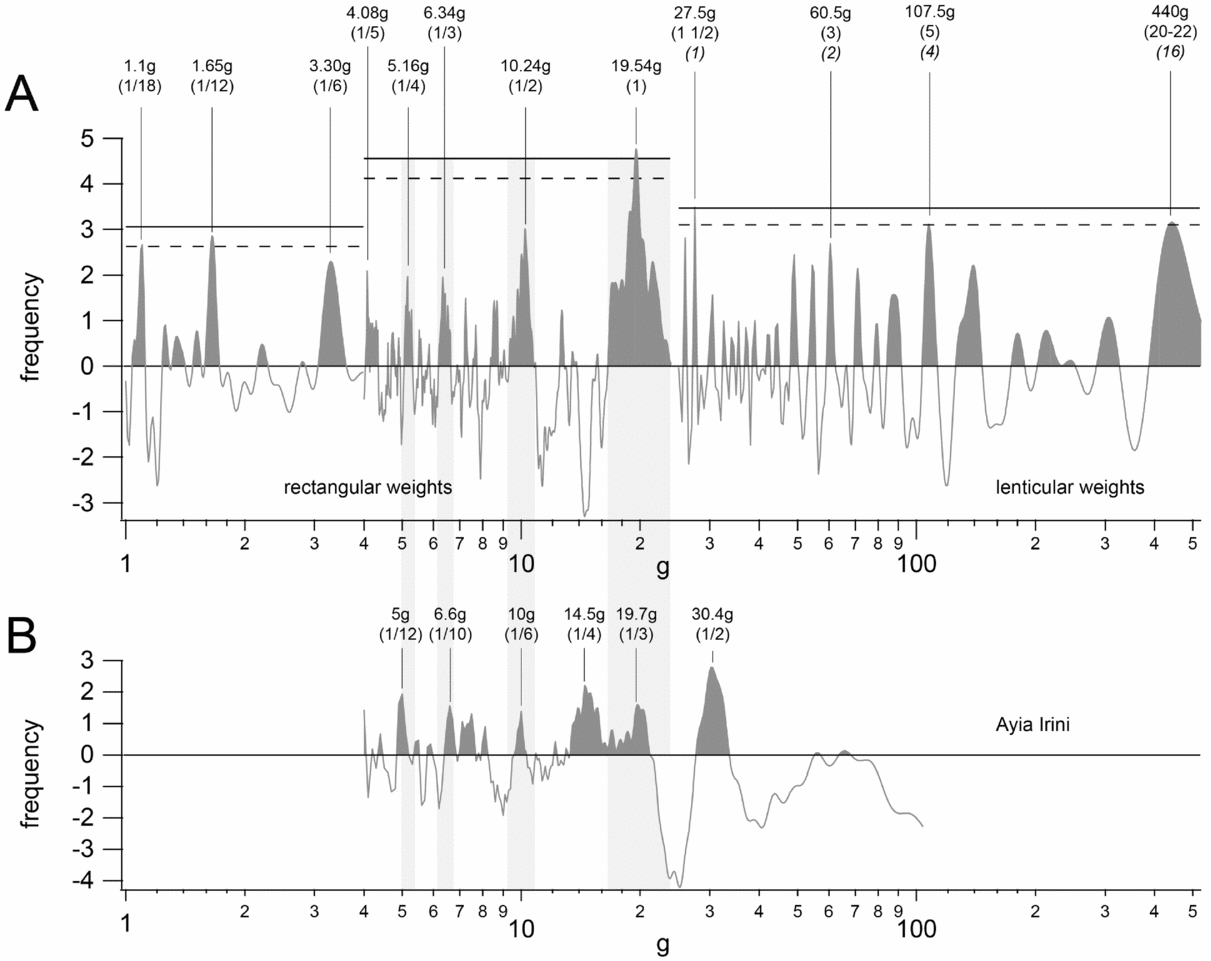
Figure 10. Cosine Quantogram Analysis comparison between the European rectangular and lenticular weight (A) and the balance weights from Ayia Irini (B); the grey bands show where the respective peaks overlap. A: the fractions in plain small text are relative to the quantum of 19.54 g; the numbers in italics are relative to the quantum at 27.5 g. B: the fractions are relative to the Aegean unit of c. 61–65 g. The CQA is displayed using a logarithmic scale, since the concentration of the peaks in the lower range would make the graph otherwise unreadable.
Sphendonoid weights
A single ‘sphendonoid’ weight with flat base (137.46 g) is attested in the Ausonio I phase on the Acropolis of Lipari (c. 1350–1200 bc). The type is extremely common in the central and eastern Mediterranean, and is attested at both Uluburun and Cape Gelydonia (Fig. 7B). To date, only one further sphendonoid weight is known in pre-literate Europe, in the grave of Migennes (Roscio et al. Reference Roscio, Delor and Muller2011; identified by Rahmstorf Reference Rahmstorf, Nessel, Heske and Brandherm2014a, 3, 13). In this case, the sample is not large enough for statistical tests, and the identification must rely solely on typology and contextual associations.
Contexts
The site on the acropolis of Lipari is a multi-stratified settlement with four superimposed building phases (Bernabò Brea & Cavalier Reference Bernabò Brea and Cavalier1980); potential balance weights are present in all occupation phases, except one (Milazzese phase, c. 1500–1350 bc). In the first phase (Capo Graziano phase, c. 2300–1500 bc), two groups of three weights come from two of the best preserved houses, while another is associated with the casting-mould of an axe (Fig. 11A). In the Ausonio I phase (c. 1350–1200 bc), a rectangular weight is associated with the sphendonoid weight (Fig. 11B). In the last occupation phase (Ausonio II, c. 1200–950 bc), a pair of rectangular weights is associated with a lenticular weight in the largest house of the settlement, in association with a casting mould and also with a hoard containing approximately 75 kg of copper ingots and scrap metal (Fig. 11C).
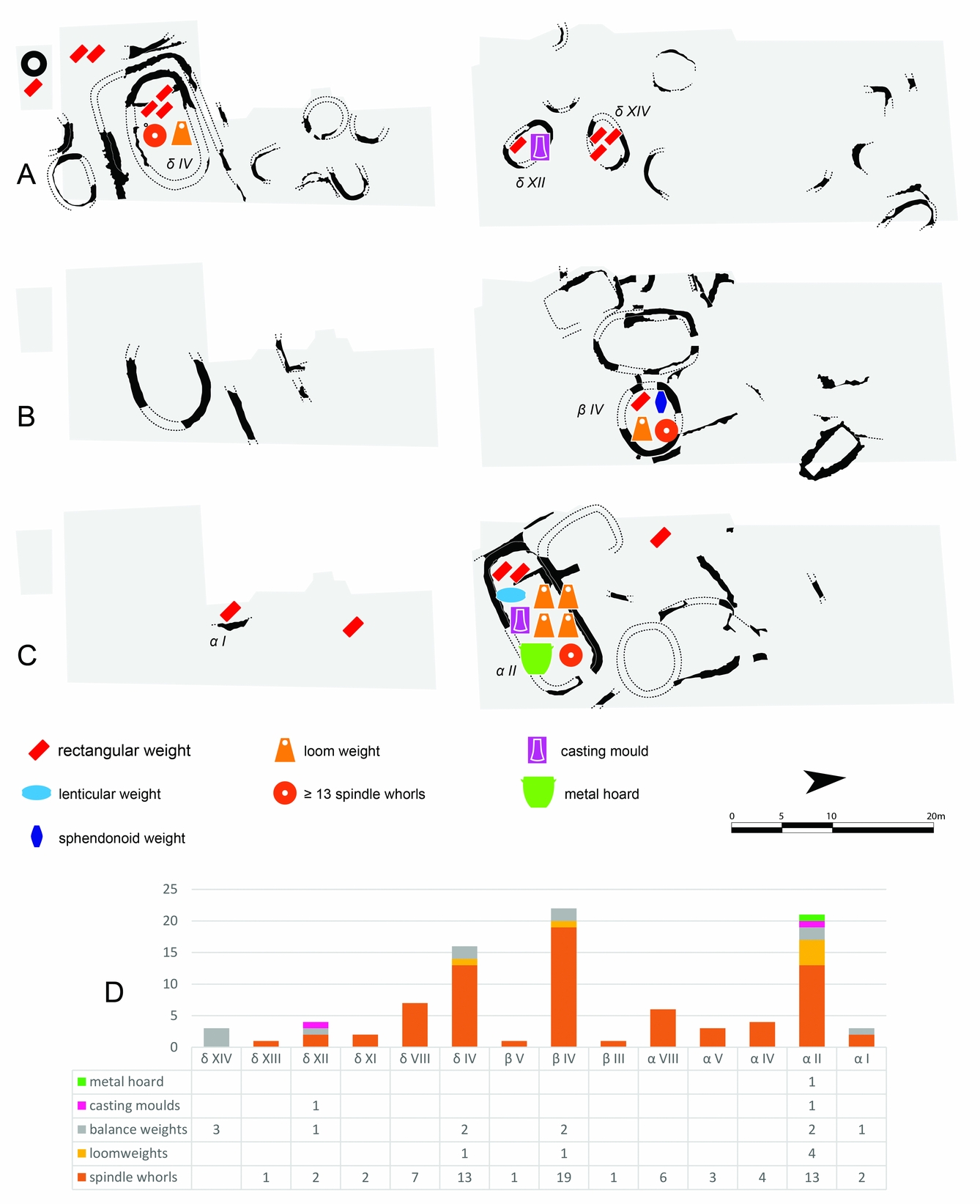
Figure 11. Lipari, Acropolis. A–C: Distribution of potential balance weights and of the evidence related to metalworking, metal trade and textile production. The position of the symbols is not accurate, having the main purpose of showing which materials were found inside the houses. (A) Capo Graziano phase (c. 2300–1500 bc); (B) Ausonio I phase (c. 1350–1200 bc); (C) Ausonio II phase (c. 1200–950 bc). (D) quantification of different classes of materials inside the houses. The Greek letters identify the different phases of the settlement, from the earliest (δ) to the latest (α).
Textile tools also show meaningful patterns of association. All the loom weights found in the settlement are always associated with potential balance weights. The number of spindle whorls inside houses normally ranges between 1 and 7 exemplars; there are only three houses—one for each phase—in which the spindle whorls range between 13 and 19 exemplars: such large numbers of spindle whorls are always associated with loom weights and potential balance weights. Finally, in the site of Portella di Salina, two lenticular weights were found in the same structure (R2), in association with a tin ingot and a casting mould (Bettelli & Cardarelli Reference Bettelli, Cardarelli and Martinelli2010).
To summarize, in the Aeolian Islands potential weights often occur in small sets inside houses, and are significantly associated with evidence of metal working, metal hoarding and textile production.
In central Europe, a set of rectangular weights is associated with two balance beams in the Late Bronze Age burial of Migennes, together with metallurgy-related working tools and small pieces of scrap gold and bronze (Roscio et al. Reference Roscio, Delor and Muller2011). Balance beams, rectangular weights and scrap gold/bronze represent a recurrent set of associations in LBA burials, possibly related to social figures dealing in metal trade (Pare Reference Pare1999). Finally, lenticular weights are frequently associated, in central and eastern Europe, with metal-working facilities in settlements (Horst Reference Horst1981; Vrdoljak & Stašo Reference Vrdoljak and Stašo1995) and with casting moulds in burials (Schmalfuß Reference Schmalfuß2007).
Discussion
Typology
The study of the Aeolian materials highlights the presence in the archipelago of at least two standard types of potential balance weights. Both the rectangular and the lenticular types represent peculiar European shapes, with a distribution spanning from southern Italy to central Europe. The rectangular type, in particular, is very common in Europe and only scarcely documented in the Mediterranean, which may lead to the hypothesis that the rectangular weights attested at Uluburun and Cape Gelydonia have a western origin. Finally, the presence of a single sphendonoid weight—a type widespread in the Eastern Mediterranean and extremely rare in Europe—might represent a residual trace of direct transactions with Mediterranean traders.
Rectangular weights are generally plain objects, but a few of them present a hole towards the top end. Such a feature suggests slightly different functions for the two variants. The presence of a hanging hook is a common feature in balance weights. Its use is described in cuneiform texts (Peyronel Reference Peyronel, Ascalone and Peyronel2011): a single weight hanging from one arm of the balance can be used as a counterweight, in order to weigh different quantities repeatedly, against a fixed amount of mass. The hanging hook is also very common in a type of pear-shaped weights, widespread in northern Italy and the Alpine region in the Middle and Late Bronze Age (Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bellintani, Corti and Giordani2001). Sometimes the insertion of a metal ring is documented in perforated weights (e.g. Feth Reference Feth, Nessel, Heske and Brandherm2014; Kulakoğlu Reference Kulakoğlu, Çiğdem, Horowitz and Gilbert2017; Pulak Reference Pulak1996); the rectangular weights, however, never present traces of metal inside the hole, and thus it is possible that they were simply held by a cord. Furthermore, the association with textile tools in the Aeolian Islands might raise the doubt that these objects are in fact loom weights. However, many clay loom weights with the typical truncated-pyramid shape are documented as well, which leads us to exclude this function for the stone objects.
The circular indentation on the heaviest rectangular weight (Fig. 5.15) might be either an aborted perforation, or some kind of quantity mark. In both cases, the attempted perforation would not have affected the mass of the object in any significant way: the object is quite massive (469.41 g), and any weight loss deriving from the perforation would have been much smaller than the commonly accepted error margin of ±5 per cent. The possibility of the existence of quantity marks, on the other hand, cannot be verified, since the occurrence of possible signs in potential balance weights in pre-literate Europe is still too rare.
The annular groove of some of the lenticular weights might have been used to fasten a cord, thus suggesting a pendent position. However, the exemplars from the Aeolian Islands and Sardinia, and several exemplars from northern Italy and the Alpine region have a flat surface, which makes them rather closer to the flat variant of the ‘domed’ weights from the Eastern Mediterranean.
Metrology
Statistical analyses support the balance-weight hypothesis for both rectangular and lenticular weights. The two different types appear to produce a logical sequence of multiples of a common system (Fig. 10A). If we choose the value of 19.54 g as a reference, we obtain a sequence of 1/12–1/6–1/5–1/4–1/3–1/2 for the lower part of the series. The higher range presents a series of very well-fitting multiples of the highest peak (27.5 g), that can be still correlated to the quantum of 19.54 g, for a sequence of 1½, 3, 5 and 20–22. The highest quantum (440 g) is too big to be directly compared, since the standard error distribution of 440 g (i.e. ±5 per cent = ±22 g) is bigger than 19.54, and therefore some uncertainty can persist on the classification of its fractional value.
Comparison between the quantogram of the European sample and that of the balance weights of Ayia Irini highlights several similarities (n = 51; range = 12–390 g, excluding six outliers between 506 g and 1615 g) (Fig. 10B). The peaks of the European system match meaningful fractions of the Aegean one at the values of c. 5.16 g, c. 7.22 g, c. 10.24 g and c. 19.54 g, corresponding, respectively, to c. 1/12, c. 1/9, c. 1/6 and c. 1/3 of the Aegean unit of c. 58–65 g (Petruso Reference Petruso1992). The higher and the lower values do not produce notable peaks, but this depends on the sample being composed of mid-range weights.
The statistical dispersions of the peaks systematically overlap, showing that the two systems share common multiples and fractions: this means that, regardless of the theoretical unit, such systems could be easily converted into each other, with a negligible error (Ialongo et al. Reference Ialongo, Vacca and Peyronel2018a). The ‘matching-points’ between the European and the Aegean systems provide convenient conversion factors, of which the Bronze Age traders must have been aware. Hence, previous suggestions about the similarity between the European and the Aegean systems are confirmed (Cardarelli et al. Reference Cardarelli, Pacciarelli, Pallante, Bellintani, Corti and Giordani2001; Pare Reference Pare1999), even though proving a direct dependency is beyond the capabilities of the method. Whether the identification of a theoretical unit may or may not be the point, the results show that the Mediterranean and European systems were largely compatible. Moreover, in the framework of a ‘globalized’ exchange (Earle et al. Reference Earle, Ling, Uhnèr, Stos-Gale and Melheim2015; Vandkilde Reference Vandkilde2016), one should not rule out the possibility that even the eastern systems may have been influenced by the European ones.
Contexts
The types of balance weights discussed in this article are systematically associated, in the LBA of central and eastern Europe, with balance beams, casting moulds, metal-working tools, metal-working facilities and gold/bronze scraps, both in burials and in settlements (Horst Reference Horst1981; Pare Reference Pare1999; Roscio et al. Reference Roscio, Delor and Muller2011; Schmalfuß Reference Schmalfuß2007; Vrdoljak & Stašo Reference Vrdoljak and Stašo1995). In the Aeolian Islands, the potential balance weights regularly occur in small sets inside houses and are systematically associated with evidence of metal trade (tin ingot and metal hoard), metallurgy (casting moulds) and textile production (loom weights and high amounts of spindle whorls) (Fig. 11). Hence, weighing equipment in Bronze Age Europe is systematically associated with those economic activities that are most expected to be relying on quantity-based exchange.
Both metallurgical and textile production require means to assess the value of incoming raw materials and outgoing finished products. It can be argued that the ‘added value’ of specialized craftsmanship might not determine a mark-up to the purchase value of a crafted product, since other immaterial factors—such as the symbolic meaning of the object or the social prerogatives of the giver—can concur in shaping the perceived value of an object being exchanged (Brück & Fontijn Reference Brück, Fontijn, Fokkens and Harding2013). In any case, this can hardly apply to raw commodities, whose economic value must be at least equal to the amount of labour required for their production: we do not know whether the local production of wool, in the Aeolian Islands, was enough to support local textile craft entirely, but certainly the metallurgical activities had to be supplied through external trade, and there is hardly any way to assess the value of a shipment of raw metal other than by its weight.
The spatial distribution indicates that weighing equipment occurs inside one or two houses per phase, suggesting that it was related to trade-dependent activities that were handled within households, the latter not necessarily intended as mere physical spaces but also in the sense of co-operative kinship-based economic units. The clustered distribution of balance weights, textile tools, casting moulds and hoards suggests that not every household was equally engaged in trade-dependent production. Interpretive models of the diachronic development of the Aeolian society in the broader framework of Southern Italy describe an increasing stratification, with specialized craftsmen eventually becoming attached to emerging elites (Peroni Reference Peroni1996). In this perspective, the large house α II in the last occupation layer on the acropolis of Lipari might provide an example of the incipient centralization of some trade-dependent economic activities (Fig. 11C). The presence of the under-floor hoard, with 75 kg of scraps and ingots, hints at the capacity of a single household to gather and dispose of substantial quantities of raw metal that had to be acquired through external trade.
The evidence is substantially in line with the documentation from private contexts in the Aegean and the Near East (see above, ‘The identification of balance weights’). All considered, it seems plausible that one of the basic purposes of weight-based trade was to exchange raw materials to be transformed into finished products; at the same time, weight-based exchange was also likely employed to transfer transiting commodities to external traders, and vice versa. The evidence suggests that trade-dependent economic activities were handled within a few selected economic units. While most households in a typical Bronze Age village would tend to focus on staple production, a few of them may have invested in trade-dependent production, providing services for the community and seeking marginal profit at the same time.
The hypothesis of a weight-based trade managed within households encourages reflection about its agents. In the case, for instance, of metal trade—one of the largest sectors of the Bronze Age economy, largely dependent on long-distance exchange—the economic cycle of a single mass of copper would be articulated into at least three basic phases: extraction, transportation and manufacture (e.g. Earle et al. Reference Earle, Ling, Uhnèr, Stos-Gale and Melheim2015). In a basic model, in which a different agent carries out each phase, we would be dealing theoretically with a miner, a merchant and an artisan, respectively. This, however, does not fully account for all the possible combinations. In a simplified instance, for example, the same agent can be responsible for more than one phase. On the other hand, transportation and manufacture can take place repeatedly and indefinitely, each time carried out by a different agent; not to mention the possible existence of supervisors, appointed with the duty of overseeing the fairness of transactions. In other words, the life-cycle of a single mass of copper implies an indefinite number of instances of weight-based exchange, involving different agents with different skills, purposes and social extractions: a highly varied range of socio-economic figures effectively connected in a seamless flow by weighing technology as a means to quantify exchange values.
Future research will help clarify whether the agents behind the Aeolian evidence were crafters, shopkeepers, seafaring merchants, supervisors, or a mix of different figures. Nonetheless, the evidence suggests that such figures may be less elusive, in pre-literate Europe, than one generally thinks.
Conclusions
The analysed sample of potential balance weights from Bronze Age Europe meets the expectations set for typological, metrological and contextual characteristics. To summarize: 1) balance weights have standardized shapes, widespread across Europe, do not normally show systematic use wear and are often realized in materials unsuitable for working tools; 2) the statistical tests are significant, and highlight a consistent system of multiples and fractions that is compatible with sets of balance weights widespread across Europe; furthermore, the European weight system is largely compatible with other Mediterranean standards, regardless of whether or not they share the same unit; 3) balance weights are systematically associated, in Europe, with balance beams and with evidence of metal trade, metallurgy and textile production; 4) the evidence from the Aeolian Islands suggests that balance weights were employed for trade-dependent production by a few selected households.
The evidence illustrated in this paper is but a small portion of what could be potentially available to research, but first it is necessary to raise more attention around the problem of an independent metrology for pre-literate Bronze Age Europe. Nonetheless, a few general traits can be outlined, to be explored in future research.
Weighing equipment begins to spread in Europe in the same period in which copper, possibly along with other goods, assumes the role of a commodity proper (Pare Reference Pare, Fokkens and Harding2013; Renfrew Reference Renfrew, Papadopoulos and Urton2008). Recently, provenance studies of raw materials, in particular metals, have raised the question of a continent-wide network of commodity exchange (e.g. Ling et al. Reference Ling, Stos-Gale, Grandin, Billström, Hjärtnhner-Holdar and Persson2014; Lutz & Pernicka Reference Lutz and Pernicka2013). A striking contrast existed between the distribution of sources and products: the former were rare, concentrated and unevenly distributed, the latter nearly ubiquitous. This might indicate that regional economies developed a specialization in the production of locally abundant raw materials, for which a high demand existed elsewhere, while relying on external trade to acquire commodities that were locally lacking, or simply too costly to produce (Earle et al. Reference Earle, Ling, Uhnèr, Stos-Gale and Melheim2015). The disequilibrium in the relative cost of producing and importing different commodities, at a continental scale, was probably accompanied by the emergence of regionally differentiated, socially acknowledged, yet fluctuating perceptions of costs and gains: i.e. different value systems that had to be converted in order to make cross-regional exchange possible. The ‘commodification’ of goods was probably accompanied by the development of a cross-cultural frame of reference for the quantification of their value (Pare Reference Pare, Fokkens and Harding2013). In the framework of a continent-wide circulation of commodities and people (Harding Reference Harding, Fokkens and Harding2013; Vandkilde Reference Vandkilde2016), uniform weight systems would have greatly facilitated cross-cultural trade.
The Aeolian evidence suggests that this process started at least as early as the first half of the second millennium bc in pre-literate Bronze Age Europe. However, the metrological field of pre-literate Europe is still very young, and thus the earliest attestation known is not necessarily the earliest ever; as research on balance weights progresses, it is not unlikely that new contexts will be identified, further raising this chronological limit. Before we can seriously speak of ‘the earliest’ weight systems, therefore, it is crucial to identify new contexts and shapes, map them out and discuss the reciprocal differences and similarities.
Acknowledgements
This work was supported by the European Research Council under the European Union's Horizon 2020 Framework Programme and was carried out within the scope of the ERC-2014-CoG ‘WEIGHTANDVALUE: Weight metrology and its economic and social impact on Bronze Age Europe, West and South Asia’, based at the Georg-August-Universität, Göttingen, Germany [Grant no. 648055], Principal Investigator: Lorenz Rahmstorf. Access to the materials was granted by: Museo Archeologico Regionale Eoliano ‘Luigi Bernabò Brea’, director M.A. Mastelloni, appointed official M.C. Martinelli; Soprintendenza Archeologia, Belle Arti e Paesaggio per le Province di Sassari e Nuoro, Soprintendente F. Di Gennaro, appointed officials N. Canu and A. Sanciu; Polo Museale della Sardegna, director G. Damiani, appointed officials M. Giorgio and M. Puddu; Museo Archeologico di Dorgali, director G. Pisanu and curator M.G. Corrias; the excavation team of Monte Croce-Guardia, director A. Cardarelli; the excavation team of Coppa Nevigata, directors A. Cazzella and G. Recchia; the excavation team of Oratino, director V. Copat; the excavation team of Nuraghe Sant'Imbenia, director M. Rendeli; the excavation team of Nuraghe Palmavera, director A. Moravetti. My special gratitude goes to Maria Clara Martinelli, Alessandro Usai, Anna Depalmas and Luca Doro, for their invaluable help in accessing the materials. Finally, I am grateful to Lorenz Rahmstorf, Giulia Recchia, Agnese Vacca, Eleonore Pape, Sarah Clegg and Marco Bettelli for the stimulating discussions and helpful advice, and to the anonymous reviewers, who offered extremely detailed and knowledgeable comments.
A preliminary version of this paper was presented at the session ‘The value of all things. Value expression and value assessment in the ancient world (Europe, Near East and the Mediterranean)’, organized by A. Gorgues, L. Melheim and T. Poigt at the 2017 EAA Conference in Maastricht.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/S0959774318000392