Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T15:29:45.153Z Has data issue: false hasContentIssue false
  • English
  • Français

Chinese science: the traditional Chinese view

Published online by Cambridge University Press:  05 February 2009

Ho Peng Yoke
Get access Rights & Permissions [Opens in a new window]

Extract

In the study of Chinese science it is important to take into account the fact that there are many Chinese terms which do not convey exactly the same meanings to traditional and modern scholars. It is essential to try to put ourselves in theshoes of the former in order to have a better understanding of classical Chinese texts. Take for example the simple term shuxue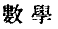, which we all take to mean ‘mathematics’. Indeed we are quite correct to call it ‘ mathematics’ when it appears in a modern text, or after the time of Li Shanlan 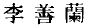(1811–1982) who first used itwhen he translated Western mathematical works into Chinese. However, when the term shuxue appears in any text written before the time of Li Shanlan it can often be dangerous to use the modern meaning of the term without circumspection. I quote a passage on the Biography of Zhang Zhong 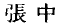from the Ming waish. contained in the Imperial Compendium Gujin tushu jicheng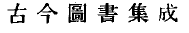 which reads:

(Zhang) Zhong was studying at his youth and presented himself at the jinshi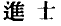 level of civil examinations. However, he failed, and whereupon he gave rein to roaming among the mountains and streams. On one occasion he came across an extraordinarily gifted person and learned shuxue from him. (Henceforth) he talked about future destiny, and was often uncanny in accuracy.

Type
Articles
Information
Bulletin of the School of Oriental and African Studies , Volume 54 , Issue 3 , October 1991 , pp. 506 - 519
Copyright
Copyright © School of Oriental and African Studies, University of London 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 As early as 1959 Joseph Needham pointed out (private communication) that theterm arithmetica in pre-modern Europe did not mean the simple calculations which go by the name of arithmetic today. See Needham, Science and civilization in China, Vol. 3 (Cambridge, 1959), 54Google Scholar. Nonetheless, as we all know, Needham’s approach is entirely that of a modern scholar.

2 In xuexingdian juan 44, tr. auct.

3 In Nanhua zhenjing (Sibu, congkan ed.) juan 5, p. 34b, tr. auctGoogle Scholar.

4 See Chourenzhuan juan I and Qian Baozong kexueshi lunwen xuanji (Beijing, 1983), 140Google Scholar.

5 See Yan, Li, ‘Sunzi suanjing buzhu’ in his Zhongguo gudai shuxue shiliao (Shanghai, 1954)Google Scholar.

6 A comprehensive study of this book is made in Lay Yong, Lam, A critical study of the Yang Hui Suan Fa (Singapore, 1974)Google Scholar. See also Needham, , Science and civilization in China, Vol. 3. 55–62Google Scholar, and Cammann, Schuyler, ‘atOld Chinese magic squares’, Sinologica, 80, 1963, 14–53Google Scholar.

7 In Yan, Li. Zhongsuanshi luncong, Vol. 3 (Shanghai, 1935)Google Scholar.

8 In Huangdi neijing suwen under ‘Sanbu liuhou lun’.

9 In juan 21, tr. auct.

10 tr. auct.

11 Sivin, Nathan, ‘Why the scientific revolution did not take place in China-or didn’t it?’, in Explorations in the history of science and technology in China (Shanghai, 1982)Google Scholar, has pointed out that what we now regard as scientific knowledge was placed under different headings by Shen Gua in his Menggi bitan.

12 cf. Science and civilization in China, Vol. 3, 119Google Scholar.

13 For the work of Qin Jiushao see Libbrecht, Ulrich, Chinese mathematics in the thirteenth century (Cambridge, Mass., 1973)Google Scholar.

14 A good example is Nathan Sivin, op. cit., n. 12.

15 See for example Yoke, Ho PengThe astronomicalchapters of the Chin Shu(Paris. 1966), 55, 56Google Scholar.

16 Hongloumeng. hui 102.

17 inch. 17.

18 Sanguo yanyi, hui 49.