We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let A be an elliptic (partial) differential operator of order 2m on a compact manifold 
with boundary Г. Let B be a normal system of m differential boundary operators on Г. Assume all manifolds and coefficients are arbitrarily smooth. We construct sesquilinear forms J in terms of which there are equivalent variational formulations of the natural boundary value problems determined by A and B with solutions in Sobolev spaces HS (M), 0 < s < 2m. Such forms are also constructed for problems with mixed boundary conditions. The variational formulation permits localization of a priori estimates and the interchange of existence and uniqueness questions between the boundary value problem and an associated adjoint problem.
Let PGL(P) be the group of projective linear transformations of the n-dimensional projective space P over a field F. A topology is given on F, and it is assumed that F is locally-compact; PGL(P) is endowed with the quotient topology from the canonical projection map GL(n, F) → PGL(P), where
.
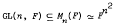For any given k, it is shown that the set of k–tuples (g1, g2, … gk) ɛ PGL(P)k which freely generate a free sub-group of PGL(P) and has a nonvoid interior.