Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2025-01-03T20:19:13.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Variational formulation of higher order elliptic boundary value problems

Published online by Cambridge University Press:  17 April 2009

A.J. Pryde
A.J. Pryde
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, GPO Box 4, Canberra, ACT 2601, Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be an elliptic (partial) differential operator of order 2m on a compact manifold 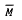with boundary Г. Let B be a normal system of m differential boundary operators on Г. Assume all manifolds and coefficients are arbitrarily smooth. We construct sesquilinear forms J in terms of which there are equivalent variational formulations of the natural boundary value problems determined by A and B with solutions in Sobolev spaces HS (M), 0 < s < 2m. Such forms are also constructed for problems with mixed boundary conditions. The variational formulation permits localization of a priori estimates and the interchange of existence and uniqueness questions between the boundary value problem and an associated adjoint problem.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 28 , Issue 1 , August 1983 , pp. 135 - 150
Copyright
Copyright © Australian Mathematical Society 1983

References

[1]Agmon, Shmuel, “The coerciveness problem for integro-differentlal forms”, J. Analyse Math. 6 (1958), 183–223.Google Scholar
[2]Aubin, Jean-Pierre, Approximation of elliptic boundary-value problems (Pure and Applied Mathematics, 26. John Wiley & Sons, New York, London, Sydney, 1972).Google Scholar
[3]Grubb, Gerd, “On coerciveness and semiboundedness of general boundary problems”, Israel J. Math. 10 (1971), 32–95.Google Scholar
[4]Lions, J.L., Equations differentielles operationnelles et problèms aux limites (Die Grundlehren der mathematischen Wissenschaften, 111. Springer-Verlag, Berlin, Gottingen, Heidelberg, 1961).Google Scholar
[5]Lions, J.L. et Magenes, E., Problèmes aux limites non homogènes et applications, Volume 1 (Travaux et Recherches Mathematiques, 17. Dunod, Paris, 1968).Google Scholar
[6]McIntosh, Alan G.R., “Bilinear forms in Hilbert space”, J. Math. Mech. 19 (1969/1970), 1027–1045.Google Scholar
[7]Mclntosh, Alan, “Second-order properly elliptic boundary value problems on irregular plane domains”, J. Differential Equations 34 (1979), 361–392.Google Scholar
[8]Peetre, Jaak, “Another approach to elliptic boundary problems”, Comm. Pure Appl. Math. 14 (1961), 711–731.Google Scholar
[9]Pryde, A.J., ”The five lemma for Banach spaces”, Proc. Amer. Math. Soc. 65 (1977), 37–43.Google Scholar
[10]Pryde, A.J., “Higher order elliptic boundary value problems in spaces with homogeneous norms”, J. Austral. Math. Soc. Ser. A 31 (1981), 92–113.Google Scholar
[11]Schechter, Martin, “General boundary value problems for elliptic partial differential equations”, Comm. Pure Appl. Math. 12 (1959), 457–486.CrossRefGoogle Scholar