Hostname: page-component-55f67697df-xq6d9 Total loading time: 0 Render date: 2025-05-11T09:55:46.279Z Has data issue: false hasContentIssue false
  • English
  • Français

WHEN IS THE INTEGRAL CLOSURE COMPARABLE TO ALL INTERMEDIATE RINGS

Part of: Chain conditions, finiteness conditions Ring extensions and related topics General commutative ring theory

Published online by Cambridge University Press:  19 October 2016

MABROUK BEN NASR  and
NABIL ZEIDI
MABROUK BEN NASR
Affiliation:
Department of Mathematics, Faculty of Sciences of Sfax, Sfax University, B.P. 1171, 3000 Sfax, Tunisia email [email protected]
NABIL ZEIDI*
Affiliation:
Department of Mathematics, Faculty of Sciences of Sfax, Sfax University, B.P. 1171, 3000 Sfax, Tunisia email [email protected]
*
✉ [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 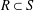$R\subset S$ be an extension of integral domains, with 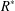$R^{\ast }$ the integral closure of 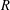$R$ in 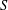$S$ . We study the set of intermediate rings between 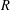$R$ and 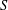$S$ . We establish several necessary and sufficient conditions for which every ring contained between 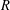$R$ and 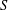$S$ compares with 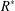$R^{\ast }$ under inclusion. This answers a key question that figured in the work of Gilmer and Heinzer [‘Intersections of quotient rings of an integral domain’, J. Math. Kyoto Univ.7 (1967), 133–150].

Keywords

intermediate ringminimal ring extensionfinite chain conditionmaximal chainnormal pairsupportconductor

MSC classification

Primary: 13B02: Extension theory
Secondary: 13A18: Valuations and their generalizations 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure 13B25: Polynomials over commutative rings 13B35: Completion 13E05: Noetherian rings and modules
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 1 , February 2017 , pp. 14 - 21
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Anderson, D. D., Dobbs, D. E. and Mullins, B., ‘The primitive element theorem for commutative algebras’, Houston J. Math. 25 (1999), 603–623; corrigendum, Houston J. Math. 28 (2002), 217–219.Google Scholar
Ayache, A., ‘A constructive study about the set of intermediate rings’, Comm. Algebra 41 (2013), 4637–4661.Google Scholar
Ayache, A. and Jarboui, N., ‘Intermediary rings in a normal pair’, J. Pure Appl. Algebra 212 (2008), 2176–2181.Google Scholar
Ben Nasr, M., ‘An answer to a problem about the number of overrings’, J. Algebra Appl. 15(6) (2016).Google Scholar
Ben Nasr, M. and Jarboui, N., ‘New results about normal pairs of rings with zero-divisors’, Ric. Mat. 63 (2014), 149–155.Google Scholar
Cahen, P. J., ‘Couple d’anneaux partageant un idéal’, Arch. Math. 51 (1988), 505–514.Google Scholar
Davis, E. D., ‘Overring of commutative ring III: normal pairs’, Trans. Amer. Math. Soc. 182 (1973), 175–185.Google Scholar
Dobbs, D. E., Mullins, B., Picavet, G. and Picavet-L’Hermitte, M., ‘On the FIP property for extensions of commutative rings’, Comm. Algebra 33 (2005), 3091–3119.CrossRefGoogle Scholar
Dobbs, D. E., Picavet, G. and Picavet-L’Hermitte, M., ‘Characterizing the ring extensions that satisfy FIP or FCP’, J. Algebra 371 (2012), 391–429.Google Scholar
Ferrand, D. and Olivier, J. P., ‘Homomorphismes minimaux d’anneaux’, J. Algebra 16 (1970), 461–471.Google Scholar
Gilmer, R., ‘Some finiteness conditions on the set of overrings of an integral domain’, Proc. Amer. Math. Soc. 131 (2002), 2337–2346.Google Scholar
Gilmer, R. and Heinzer, W., ‘Intersections of quotient rings of an integral domain’, J. Math. Kyoto Univ. 7 (1967), 133–150.Google Scholar
Griffin, M., ‘Prüfer rings with zero divisors’, J. reine angew. Math. 239/240 (1969), 55–67.Google Scholar
Picavet, G. and Picavet-L’Hermitte, M., ‘About minimal morphisms’, in: Multiplicative Ideal Theory in Commutative Algebra (eds. Brewer, J. W., Glaz, S., Heinzer, W. and Oberding, B.) (Springer, New York, 2006), 369–386.CrossRefGoogle Scholar
Jaballah, A., ‘A lower bound for the number of intermediary rings’, Comm. Algebra 27 (1999), 1307–1311.Google Scholar
Jaballah, A., ‘Finiteness of the set of intermediary rings in normal pairs’, Saitama Math. J. 17 (1999), 59–61.Google Scholar
Kaplansky, I., Commutative Rings (University of Chicago Press, Chicago, 1974), (revised edition).Google Scholar