Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T03:02:54.389Z Has data issue: false hasContentIssue false
  • English
  • Français

The Weyl functional calculus and two-by-two selfadjoint matrices

Published online by Cambridge University Press:  17 April 2009

Werner J. Ricker
Werner J. Ricker
Affiliation:
School of Mathematics, The University of New South Wales, Sydney NSW 2052, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D be a (2 × 2) matrix with distinct eigenvalues λ1 and λ2. There is a basic and well known functional equation which provides a formula for constructing the matrix g (D), for any ℂ-valued function g defined on a subset of ℂ containing {λ1,λ2}, namely .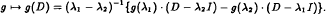

This equation is used to give a direct and transparent proof of the following fact due to Anderson: A pair of (2 × 2) selfadjoint matrices A1 and A2 commute if and only if the Weyl functional calculus of the pair (A1,A2), which is a matrix-valued distribution, has order zero (that is, is a measure).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 55 , Issue 2 , April 1997 , pp. 321 - 325
Copyright
Copyright © Australian Mathematical Society 1997

References

[1]Anderson, R.F.V., ‘The Weyl Functional calculus’, J. Funct. Anal. 4 (1969), 240–267.CrossRefGoogle Scholar
[2]Anderson, R.F.V., ‘On the Weyl functional calculus’, J. Funct. Anal. 6 (1970), 110–115.CrossRefGoogle Scholar
[3]Brenner, P., ‘The Cauchy problem for symmetric hyperbolic systems is Lp’, Math. Scand. 19 (1966), 27–37.CrossRefGoogle Scholar
[4]Jefferies, B.R.F. and Ricker, W.J., ‘Commutativity for systems of (2 × 2) selfadjoint matrices’, Linear and Multilinear Algebra 35 (1993), 107–114.CrossRefGoogle Scholar
[5]Ricker, W.J., ‘The Weyl calculus and commutativity for systems of selfadjoint matrices’, Arch. Math. 61 (1993), 173–176.CrossRefGoogle Scholar
[6]Taylor, M.E., ‘Functions of several selfadjoint operators’, Proc. Amer. Math. Soc. 19 (1968), 91–98.CrossRefGoogle Scholar
[7]Weyl, H., The theory of groups and quantum mechanics (Dover Publ., New York, 1950).Google Scholar