Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T14:26:12.437Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted estimates for fractional maximal functions related to spherical means

Published online by Cambridge University Press:  17 April 2009

Michael Cowling ,
José García-Cuerva  and
Hendra Gunawan
Michael Cowling
Affiliation:
School of Mathematics, University of New South Wales, Sydney NSW 2052, Australia
José García-Cuerva
Affiliation:
Departamento de Matemáticas, C-XV, Universidad Autónoma de Madrid, 28049-Madrid, Spain
Hendra Gunawan
Affiliation:
Jurusan Matematika, Institut Teknologi Bandung, Bandung 40132, Indonesia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

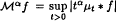We prove weighted Lp-Lq estimates for the maximal operators ℳα, given by , where μt denotes the normalised surface measure on the sphere of centre 0 and radius t in Rd. The techniques used involve interpolation and the Mellin transform. To do this, we also prove weighted Lp-Lq estimates for the operators of convolution with the kernels |·|−α−iη.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 66 , Issue 1 , August 2002 , pp. 75 - 90
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Bourgain, J., ‘Averages in the plane over convex curves and maximal operators’, J. Analyse Math. 47 (1986), 69–85.Google Scholar
[2]Cowling, M. and Mauceri, G., ‘On maximal functions’, Rend. Sem. Mat. Fis. Milano 49 (1979), 79–87.CrossRefGoogle Scholar
[3]Duoandikoetxea, J. and Vega, L., ‘Spherical means and weighted inequalities’, J. London Math. Soc. 53 (1996), 343–353.Google Scholar
[4]Gunawan, H., ‘On weighted estimates for Stein's maximal function’, Bull. Austral. Math. Soc. 54 (1996), 35–39.Google Scholar
[5]Gunawan, H., ‘Some weighted estimates for Stein's maximal function’, Bull. Malaysian Math. Soc. 21 (1998), 101–105.Google Scholar
[6]García-Cuerva, J. and de Francia, J.-L. Rubio, Weighted norm inequalities and related topics (North-Holland, Amsterdam, 1985).Google Scholar
[7]Hardy, G.H. and Littlewood, J.E., ‘A maximal theorem with function-theoretic applications’, Acta Math. 54 (1930), 81–116.CrossRefGoogle Scholar
[8]Harboure, E., Macias, R.A. and Segovia, C., ‘Extrapolation results for classes of weights’, Amer. J. Math. 110 (1988), 383–397.CrossRefGoogle Scholar
[9]Muckenhoupt, B., ‘Weighted norm inequalities for the Hardy maximal function’, Trans. Amer. Math. Soc. 165 (1972), 207–227.Google Scholar
[10]Muckenhoupt, B. and Wheeden, R., ‘Weighted norm inequalities for fractional integrals’, Trans. Amer. Math. Soc. 192 (1974), 261–275.CrossRefGoogle Scholar
[11]Oberlin, D.M., ‘Operators interpolating between Riesz potentials and maximal operators’, Illinois J. Math. 33 (1989), 143–152.Google Scholar
[12]de Francia, J.-L. Rubio, ‘Weighted norm inequalities for homogeneous families of operators’, Trans. Amer. Math. Soc. 275 (1983), 781–790.Google Scholar
[13]Sawyer, E.T., ‘Weighted norm inequalities for fractional maximal operators’, CMS Conf. Proc. 1 (1981), 283–309.Google Scholar
[14]Sawyer, E.T., ‘A characterization of a two weight norm inequality for maximal operators’, Studia Math. 75 (1982), 1–11.Google Scholar
[15]Stein, E.M., Singular integrals and differentiability properties of functions (Princeton Univ. Press, Princeton, N.J., 1970).Google Scholar
[16]Stein, E.M., ‘Maximal functions: spherical means’, Proc. Nat. Acad. Sci. U.S.A. 73 (1976), 2174–2175.Google Scholar
[17]Stein, E.M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces (Princeton Univ. Press, Princeton, N.J., 1971).Google Scholar
[18]Titchmarsh, E.C., The theory of functions, (2nd edition) (Oxford Univ. Press, New York, 1939).Google Scholar