Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rmoutil, Martin
2017.
Norm-attaining functionals need not contain 2-dimensional subspaces.
Journal of Functional Analysis,
Vol. 272,
Issue. 3,
p.
918.
García-Pacheco, Francisco Javier
2021.
Lineability of the set of supporting vectors.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 115,
Issue. 2,


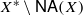 of non-norm-attaining functionals on
of non-norm-attaining functionals on 