Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Morris, Sidney A.
1970.
Varieties of topological groups III.
Bulletin of the Australian Mathematical Society,
Vol. 2,
Issue. 2,
p.
165.
Morris, Sidney A.
1970.
Varieties of topological groups.
Bulletin of the Australian Mathematical Society,
Vol. 3,
Issue. 3,
p.
429.
Morris, Sidney A.
1970.
Varieties of topological groups II.
Bulletin of the Australian Mathematical Society,
Vol. 2,
Issue. 1,
p.
1.
Morris, Sidney A.
1971.
Free products of topological groups.
Bulletin of the Australian Mathematical Society,
Vol. 4,
Issue. 1,
p.
17.
Morris, Sidney A.
1971.
A topological group characterization of those locally convex spaces having their weak topology.
Mathematische Annalen,
Vol. 195,
Issue. 2,
p.
330.
Chen, Su-Shing
and
Morris, Sidney A.
1972.
Varieties of topological groups generated by Lie groups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 18,
Issue. 1,
p.
49.
Mack, John
Morris, Sidney A.
and
Ordman, Edward T.
1973.
Free topological groups and the projective dimension of a locally compact abelian group.
Proceedings of the American Mathematical Society,
Vol. 40,
Issue. 1,
p.
303.
Brooks, M. S.
Morris, Sidney. A.
and
Saxon, Stephen. A.
1973.
Generating varieties of topological groups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 18,
Issue. 3,
p.
191.
Morris, Sidney A.
1973.
Varieties of topological groups and left adjoint functors.
Journal of the Australian Mathematical Society,
Vol. 16,
Issue. 2,
p.
220.
Hardy, J. P. L.
Morris, Sidney A.
and
Thompson, H. B.
1976.
Applications of the Stone-Čech compactification to free topological groups.
Proceedings of the American Mathematical Society,
Vol. 55,
Issue. 1,
p.
160.
Taylor, Walter
1977.
Varieties of topological algebras.
Journal of the Australian Mathematical Society,
Vol. 23,
Issue. 2,
p.
207.
Thomas, Barbara V. Smith
1977.
CATEGORIES OF TOPOLOGICAL GROUPS.
Quaestiones Mathematicae,
Vol. 2,
Issue. 1-3,
p.
355.
Hardy, J. P. L.
and
Morris, Sidney A.
1977.
A Note on Free Topological Groupoids.
Mathematische Nachrichten,
Vol. 77,
Issue. 1,
p.
177.
Morris, Sidney A.
and
Nickolas, Peter
1980.
The extension of norms on subgroups of free topological groups.
Proceedings of the American Mathematical Society,
Vol. 80,
Issue. 1,
p.
185.
Day, Jane M.
1982.
Compact semilattice quotients which separate idempotent ℐ-classes.
Semigroup Forum,
Vol. 24,
Issue. 1,
p.
341.
Katz, Eli
and
Morris, Sidney A.
1982.
On endomorphisms of abelian topological groups.
Proceedings of the American Mathematical Society,
Vol. 85,
Issue. 2,
p.
181.
Mukhin, Yu. N.
1985.
Topological groups.
Journal of Soviet Mathematics,
Vol. 28,
Issue. 6,
p.
825.
Arkhangel'skii, A. V.
1989.
Algebraic objects generated by topological structure.
Journal of Soviet Mathematics,
Vol. 45,
Issue. 1,
p.
956.
Shakhmatov, Dmitrii B
1990.
Imbeddings into topological groups preserving dimensions.
Topology and its Applications,
Vol. 36,
Issue. 2,
p.
181.
Choban, M.M.
1993.
Some topics in topological algebra.
Topology and its Applications,
Vol. 54,
Issue. 1-3,
p.
183.
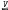 of topological groups and of a free topological group F(X,
of topological groups and of a free topological group F(X, 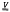 ) of
) of 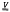 on a topological space X as generalizations of the analogous concepts in the theory of varieties of groups. Necessary and sufficient conditions for F(X,
on a topological space X as generalizations of the analogous concepts in the theory of varieties of groups. Necessary and sufficient conditions for F(X, 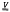 ) to exist are given and uniqueness is proved. We say the topological group FM,(X) is moderately free on X if its topology is maximal and it is algebraically free with X as a free basis. We show that FM(X) is a free topological group of the variety it generates and that if FM(X) is in
) to exist are given and uniqueness is proved. We say the topological group FM,(X) is moderately free on X if its topology is maximal and it is algebraically free with X as a free basis. We show that FM(X) is a free topological group of the variety it generates and that if FM(X) is in 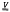 then it is topologically isomorphic to a quotient group of F(X,
then it is topologically isomorphic to a quotient group of F(X, 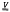 ). It is also shown how well known results on free (free abelian) topological groups can be deduced. In the algebraic theory there are various equivalents of a free group of a variety. We examine the relationships between the topological analogues of these. In the appendix a result similar to the Stone-Čech compactification is proved.
). It is also shown how well known results on free (free abelian) topological groups can be deduced. In the algebraic theory there are various equivalents of a free group of a variety. We examine the relationships between the topological analogues of these. In the appendix a result similar to the Stone-Čech compactification is proved.