Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-18T15:21:46.923Z Has data issue: false hasContentIssue false
  • English
  • Français

Varieties of soluble groups and a dichotomy of P. Hall

Published online by Cambridge University Press:  17 April 2009

J.R.J. Groves
J.R.J. Groves
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let denote the variety of all abelian groups and, for each prime p, let 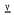p be the variety of all elementary abelian p-groups. Let be a subvariety of a product of (finitely many) varieties each of which is either soluble or Cross.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 5 , Issue 3 , December 1971 , pp. 391 - 410
Copyright
Copyright © Australian Mathematical Society 1971

References

[1]Bryant, Roger M., “On some varieties of groups”, Bull. London Math. Soc. 1 (1969), 60–64.CrossRefGoogle Scholar
[2]Bryce, R.A., “Metabelian groups and varieties”, Philos. Trans. Roy. Soc. London Ser. A 266 (1970), 281–355.Google Scholar
[3]Groves, J.R.J., “On varieties of soluble groups”, Bull. Austral. Math. Soc. 5 (1971), 95–109.CrossRefGoogle Scholar
[4]Groves, J.R.J., “Varieties of soluble groups”, (Ph.D. thesis, Australian National University, Canberra, 1971).CrossRefGoogle Scholar
[5]Hall, P., “Finiteness conditions for soluble groups”, Proc. London Math. Soc. (3) 4 (1954), 419–436.Google Scholar
[6]Hall, P., “Some sufficient conditions for a group to be nilpotent”, Illinois J. Math. 2 (1958), 787–801.CrossRefGoogle Scholar
[7]Hall, P., “On the finiteness of certain soluble groups”, Proc. London Math. Soc. (3) 9 (1959), 595–622.CrossRefGoogle Scholar
[8]Hall, P., “The Frattini subgroups of finitely generated groups”, Proc. London Math. Soc. (3) 11 (1961), 327–352.CrossRefGoogle Scholar
[9]Higman, Graham, “Some remarks on varieties of groups”, Quart. J. Math. Oxford (2) 10 (1959), 165–178.CrossRefGoogle Scholar
[10]Kovács, L.G. and Newman, M.F., “Minimal verbal subgroups”, Proc. Cambridge Philos. Soc. 62 (1966), 347–350.CrossRefGoogle Scholar
[11]Kováccs, L.G. and Newman, M.F., “Just-non-Cross varieties”, Proc. Internat. Conf. Theory of groups, Austral, flat. Univ., Canberra, 1965, 221–223 (Gordon and Breach, New York, London, Paris, 1967).Google Scholar
[12]Kovács, L.G. and Newman, M.F., “On non-Cross varieties of groups”, J. Austral. Math. Soc. 12 (1971), 129–144.CrossRefGoogle Scholar
[13]Neumann, B.H., “Groups with finite classes of conjugate elements”, Proc. London Math. Soc. (3) 1 (1951), 178–187.CrossRefGoogle Scholar
[14]Neumann, Hanna, Varieties of groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 37. Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
[15]Neumann, Peter M., “On word subgroups of free groups”, Arch. Math. 16 (1965), 6–21.CrossRefGoogle Scholar
[16]Neumann, Peter M., “A note on the direct decomposability of relatively free groups”, Quart. J. Math. Oxford (2) 19 (1968), 67–79.CrossRefGoogle Scholar
[17]Oates, Sheila, “Identical relations in groups”, J. London Math. Soc. 38 (1963), 71–78.CrossRefGoogle Scholar
[18]Robinson, Derek J.S., Infinite soluble and nilpotent groups (Queen Mary College Mathematics Notes, Mathematics Department, Queen Mary College, London, N.D. [1968]).Google Scholar
[19]Šmel'kin, A.L., “On soluble group varieties”, Soviet Math. Dokl. 9 (1968), 100–103.Google Scholar
[20]Stewart, A.G.R., “On the class of certain nilpotent groups”, Proc. Roy. Soc. London Sep. A 292 (1966), 374–379.Google Scholar