Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-21T01:21:08.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform property (K) and its related properties

Published online by Cambridge University Press:  17 April 2009

Hong-Kun Xu  and
Giuseppe Marino
Hong-Kun Xu
Affiliation:
Department of MathematicsUniversity of Durban-WestvilleDurban 4000South Africa e-mail: [email protected]
Giuseppe Marino
Affiliation:
Dipartimento di MatematicaUniversitá della CalabriaCosenzaItaly e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Banach space X is said to have uniform property (K) if there exists a constant (k ∈ [0,1) such that whenever xn ⇀ 0, ∥xn∥ → 1, and 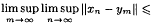we have lim sup ∥ym∥ ≤ k. This property is the uniform version of property (K) recently introduced by B. Sims (Bull. Austral. Math. Soc. 50(1994), 523–528). Sufficient conditions for uniform property (K) are given. Some examples are presented to separate various Banach space properties. Applications to nonlinear operators are also included.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 57 , Issue 1 , February 1998 , pp. 93 - 107
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Bynum, W.L., ‘Normal structure coefficients for Banach spaces’, Pacific J. Math. 86 (1980), 427–436.CrossRefGoogle Scholar
[2]Casini, E. and Maluta, E., ‘Fixed points of uniformly Lipschitzian mappings in spaces with uniformly normal structure’, Nonlinear Anal. 9 (1985), 103–106.CrossRefGoogle Scholar
[3]Day, M.M., James, R.C. and Swaminathan, S., ‘Normed linear spaces that are uniformly convex in every direction’, Canad. J. Math. 23 (1971), 1051–1059.CrossRefGoogle Scholar
[4]van Dulst, D., ‘Equivalent norms and the fixed point property for nonexpansive mappings’, J. London Math. Soc. 25 (1982), 139–144.CrossRefGoogle Scholar
[5]Garciá-Falset, J. and Lloréns-Fuster, E., ‘Normal structure and fixed point property’, Glasgow Math. J. 38 (1996), 29–37.CrossRefGoogle Scholar
[6]Garcia-Falset, J., Sims, B. and Smyth, M.A., ‘The demiclosedness principle for mappings of asymptotically nonexpansive type’, Houston J. Math. 22 (1996), 101–108.Google Scholar
[7]Jiménez-Melado, A., ‘Stability of weak normal structure in James quasi reflexive space’, Bull. Austral. Math. Soc. 46 (1992), 367–372.CrossRefGoogle Scholar
[8]Kirk, W.A., ‘Fixed point theorems for non-Lipschitzian mappings of asymptotically nonexpansive type’, Israel J. Math. 17 (1974), 339–346.CrossRefGoogle Scholar
[9]Lim, T.C., ‘Asymptotic centers and nonexpansive mappings in some conjugate spaces’, Pacific J. Math. 90 (1980), 135–143.CrossRefGoogle Scholar
[10]Lim, T.C. and Xu, H.K., ‘Fixed point theorems for asymptotically nonexpansive mappings’, Nonlinear Anal. 22 (1994), 1345–1355.CrossRefGoogle Scholar
[11]Lin, P.K., ‘Asymptotic behavior for asymptotically nonexpansive mappings’, Nonlinear Anal. 26 (1996), 1137–1141.CrossRefGoogle Scholar
[12]Lin, P.K., Tan, K.K. and Xu, H.K., ‘Demiclosedness principle and asymptotic behavior for asymptotically nonexpansive mappings’, Nonlinear Anal. 24 (1995), 929–946.CrossRefGoogle Scholar
[13]Maluta, E., ‘Uniformly normal structure and related coefficients’, Pacific J. Math. 111 (1984), 357–369.CrossRefGoogle Scholar
[14]Opial, Z., ‘Weak convergence of the sequence of successive approximations for nonexpasive mappings’, Bull. Amer. Math. Soc. 73 (1967), 591–597.CrossRefGoogle Scholar
[15]Sims, B., ‘A class of spaces with weak normal structure’, Bull. Austral. Math. Soc. 50 (1994), 523–528.CrossRefGoogle Scholar
[16]Sims, B. and Smyth, M., ‘Non-uniform conditions giving weak normal structure’, Quaestiones Math. 18 (1995), 9–19.CrossRefGoogle Scholar
[17]Tan, K.K. and Xu, H.K., ‘On fixed point theorems of nonexpansive mappings in product spaces’, Proc. Amer. Math. Soc. 113 (1991), 983–989.CrossRefGoogle Scholar
[18]Xu, H.K., ‘Geometrical coefficients of Banach spaces and nonlinear mappings’, in Recent advances on metric fixed point theory, (Benavides, T. Dominguez, Editor), Proceedings of the International Workshop on Metric Fixed Point Theory, Sevilla, Spain, September 1995 (University of Sevilla Press, 1996), pp. 161–178.Google Scholar