Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-19T06:40:40.929Z Has data issue: false hasContentIssue false
  • English
  • Français

The uniform law of large numbers for the Kaplan-Meier integral process

Published online by Cambridge University Press:  17 April 2009

Jongsig Bae  and
Sungyeun Kim
Jongsig Bae
Affiliation:
Department of Mathematics and Institute of Basic Science, SungKyunKwan University, Suwon 440–746, Korea e-mail: [email protected], [email protected]
Sungyeun Kim
Affiliation:
Department of Mathematics and Institute of Basic Science, SungKyunKwan University, Suwon 440–746, Korea e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 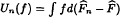be the function-indexed Kaplan-Meier integral process constructed from the random censorship model. We study a uniform version of the law of large numbers of Glivenko-Cantelli type for {Un} under the bracketing entropy condition. The main result is that the almost sure convergence and convergence in the mean of the process Un holds uniformly in ℱ. In proving the result we shall employ the bracketing method which is used in the proof of the uniform law of large numbers for the complete data of the independent and identically distributed model.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 67 , Issue 3 , June 2003 , pp. 459 - 465
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]DeHardt, J., ‘Generalizations of the Glivenko-Cantelli theorem’, Ann. Math. Statist. 42 (1971), 2050–2055.Google Scholar
[2]Kaplan, E.L. and Meier, P., ‘Nonparametric estimation from incomplete observations’, J. Amer. Statist. Assoc. 53 (1958), 457–481.CrossRefGoogle Scholar
[3]Ossiander, M., ‘A central limit theorem under metric entropy with L 2 bracketing’, Ann. Probab. 15 (1987), 897–919.Google Scholar
[4]Stute, W. and Wang, J.L., ‘The strong law under random censorship’, Ann. Statist. 21 (1993), 1591–1607.Google Scholar
[5]Stute, W., ‘The central limit theorem under random censorship’, Ann. Statist. 23 (1995), 422–439.Google Scholar
[6]Van de Geer, S., Applications of empirical process theory, Cambridge Series in Statistical and Probabilistic Mathematics (Cambridge University Press, Cambridge, U.K., 2000).Google Scholar
[7]Van der Vaart, A. and Wellner, J.A., Weak convergence and empirical processes with applications to statistics, Springer series in Statistics (Springer-Verlag, New York, 1996).Google Scholar