Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bae, Jong-Sic
and
Kim, Sung-Yeun
2006.
UNIFORM ASYMPTOTICS IN THE EMPIRICAL MEAN RESIDUAL LIFE PROCESS.
Journal of the Korean Mathematical Society,
Vol. 43,
Issue. 2,
p.
225.
Jeganathan, Pratheepa
Randrianampy, Noroharivelo V.
Paige, Robert L.
and
Trindade, A. Alexandre
2019.
An empirical saddlepoint approximation based method for smoothing survival functions under right censoring.
Canadian Journal of Statistics,
Vol. 47,
Issue. 2,
p.
238.


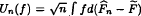 be the Kaplan-Meier integral process constructed from the random censorship model. We prove a uniform central limit theorem for {
be the Kaplan-Meier integral process constructed from the random censorship model. We prove a uniform central limit theorem for {