No CrossRef data available.
Published online by Cambridge University Press: 01 June 2008
Let K and X be compact plane sets such that 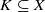 . Let P(K) be the uniform closure of polynomials on K, let R(K) be the uniform closure of rational functions on K with no poles in K and let A(K) be the space of continuous functions on K which are analytic on int(K). Define P(X,K),R(X,K) and A(X,K) to be the set of functions in C(X) whose restriction to K belongs to P(K),R(K) and A(K), respectively. Let S0(A) denote the set of peak points for the Banach function algebra A on X. Let S and T be compact subsets of X. We extend the Hartogs–Rosenthal theorem by showing that if the symmetric difference SΔT has planar measure zero, then R(X,S)=R(X,T) . Then we show that the following properties are equivalent:
. Let P(K) be the uniform closure of polynomials on K, let R(K) be the uniform closure of rational functions on K with no poles in K and let A(K) be the space of continuous functions on K which are analytic on int(K). Define P(X,K),R(X,K) and A(X,K) to be the set of functions in C(X) whose restriction to K belongs to P(K),R(K) and A(K), respectively. Let S0(A) denote the set of peak points for the Banach function algebra A on X. Let S and T be compact subsets of X. We extend the Hartogs–Rosenthal theorem by showing that if the symmetric difference SΔT has planar measure zero, then R(X,S)=R(X,T) . Then we show that the following properties are equivalent:
(i) R(X,S)=R(X,T) ;
(ii) 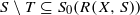 and
and 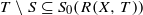 ;
;
(iii) R(K)=C(K)for every compact set 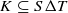 ;
;
(iv) 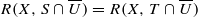 for every open set U in ℂ ;
for every open set U in ℂ ;
(v) for every p∈X there exists an open disk Dp with centre p such that 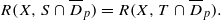
(i) A(X,S)=R(X,T) ;
(ii) 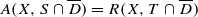 for every closed disk
for every closed disk 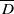 in ℂ ;
in ℂ ;
(iii) for every p∈X there exists an open disk Dp with centre p such that