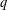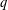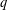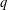Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zudilin, Wadim
2015.
Multiple q-Zeta Brackets.
Mathematics,
Vol. 3,
Issue. 1,
p.
119.
Singer, Johannes
2015.
On $q$-analogues of multiple zeta values.
Functiones et Approximatio Commentarii Mathematici,
Vol. 53,
Issue. 1,
Ebrahimi-Fard, Kurusch
Manchon, Dominique
and
Singer, Johannes
2016.
Duality and (q-)multiple zeta values.
Advances in Mathematics,
Vol. 298,
Issue. ,
p.
254.
Ebrahimi-Fard, Kurusch
Manchon, Dominique
and
Singer, Johannes
2016.
Renormalisation of q-Regularised Multiple Zeta Values.
Letters in Mathematical Physics,
Vol. 106,
Issue. 3,
p.
365.
Ebrahimi-Fard, Kurusch
Manchon, Dominique
and
Singer, Johannes
2016.
The Hopf Algebra of ($q$-)Multiple Polylogarithms with Non-positive Arguments: Table 1..
International Mathematics Research Notices,
p.
rnw128.
Singer, Johannes
2016.
On Bradley's q-MZVs and a generalized Euler decomposition formula.
Journal of Algebra,
Vol. 454,
Issue. ,
p.
92.
Bachmann, Henrik
2019.
The algebra of bi-brackets and regularized multiple Eisenstein series.
Journal of Number Theory,
Vol. 200,
Issue. ,
p.
260.
Takeyama, Yoshihiro
2020.
Derivations on the algebra of multiple harmonic q-series and their applications.
The Ramanujan Journal,
Vol. 52,
Issue. 1,
p.
41.
Bachmann, Henrik
2020.
Periods in Quantum Field Theory and Arithmetic.
Vol. 314,
Issue. ,
p.
173.
Hatsuda, Yasuyuki
and
Okazaki, Tadashi
2023.
Exact $$ \mathcal{N} $$ = 2* Schur line defect correlators.
Journal of High Energy Physics,
Vol. 2023,
Issue. 6,
Burmester, Annika
2024.
Balanced multiple q-zeta values.
Advances in Mathematics,
Vol. 439,
Issue. ,
p.
109487.
Takeyama, Yoshihiro
2024.
A q-analogue of symmetric multiple zeta value.
The Ramanujan Journal,
Vol. 63,
Issue. 1,
p.
209.
Hatsuda, Yasuyuki
and
Okazaki, Tadashi
2024.
Large N and large representations of Schur line defect correlators.
Journal of High Energy Physics,
Vol. 2024,
Issue. 1,