Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-22T03:31:25.479Z Has data issue: false hasContentIssue false
  • English
  • Français

TWO PROBLEMS CONCERNING IRREDUCIBLE ELEMENTS IN RINGS OF INTEGERS OF NUMBER FIELDS

Part of: Algebraic number theory: global fields Multiplicative number theory

Published online by Cambridge University Press:  02 March 2017

PAUL POLLACK  and
LEE TROUPE
PAUL POLLACK
Affiliation:
Department of Mathematics, Boyd Graduate Studies Research Center, University of Georgia, Athens, GA 30602, USA email [email protected]
LEE TROUPE*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, British Columbia V6T 1Z2, Canada email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 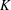$K$ be a number field with ring of integers 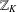$\mathbb{Z}_{K}$. We prove two asymptotic formulas connected with the distribution of irreducible elements in 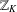$\mathbb{Z}_{K}$. First, we estimate the maximum number of nonassociated irreducibles dividing a nonzero element of 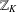$\mathbb{Z}_{K}$ of norm not exceeding $x$ (in absolute value), as 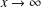$x\rightarrow \infty$. Second, we count the number of irreducible elements of 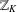$\mathbb{Z}_{K}$ of norm not exceeding $x$ lying in a given arithmetic progression (again, as 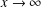$x\rightarrow \infty$). When 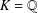$K=\mathbb{Q}$, both results are classical; a new feature in the general case is the influence of combinatorial properties of the class group of 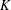$K$.

Keywords

irreduciblenumber fieldfactorisationray classDavenport constant

MSC classification

Primary: 11R27: Units and factorization
Secondary: 11N37: Asymptotic results on arithmetic functions 11N45: Asymptotic results on counting functions for algebraic and topological structures
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 44 - 58
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

Research of the first author is supported by NSF award DMS-1402268.

References

Childress, N., Class Field Theory, Universitext (Springer, New York, 2009).Google Scholar
Geroldinger, A. and Halter-Koch, F., Non-Unique Factorizations: Algebraic, Combinatorial and Analytic Theory, Pure and Applied Mathematics (Boca Raton), vol. 278 (Chapman and Hall/CRC, Boca Raton, FL, 2006).CrossRefGoogle Scholar
Geroldinger, A. and Ruzsa, I. Z., Combinatorial Number Theory and Additive Group Theory, Advanced Courses in Mathematics. CRM Barcelona (Birkhäuser, Basel, 2009).Google Scholar
Hardy, G. H. and Ramanujan, S., ‘The normal number of prime factors of a number n ’, Quart. J. Math. 48 (1917), 76–92.Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 5th edn (Oxford University Press, Oxford, 2000).Google Scholar
Landau, E., ‘Über Ideale und Primideale in Idealklassen’, Math. Z. 2(1–2) (1918), 52–154.CrossRefGoogle Scholar
Narkiewicz, W., Elementary and Analytic Theory of Algebraic Numbers, 3rd edn, Springer Monographs in Mathematics (Springer, Berlin, 2004).CrossRefGoogle Scholar
Pollack, P., ‘An elemental Erdős–Kac theorem for algebraic number fields’, Proc. Amer. Math. Soc. 145(3) (2017), 971–987.Google Scholar
Rémond, P., ‘Étude asymptotique de certaines partitions dans certains semi-groupes’, Ann. Sci. Éc. Norm. Supér. (3) 83 (1966), 343–410.Google Scholar