Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T22:57:18.746Z Has data issue: false hasContentIssue false
  • English
  • Français

A TRUNCATED IDENTITY OF EULER AND RELATED $q$-CONGRUENCES

Part of: Combinatorics Elementary number theory

Published online by Cambridge University Press:  08 April 2020

JI-CAI LIU Open the ORCID record for JI-CAI LIU [Opens in a new window]  and
ZHONG-YU HUANG
JI-CAI LIU*
Affiliation:
Department of Mathematics,Wenzhou University, Wenzhou325035, PR China email [email protected]
ZHONG-YU HUANG
Affiliation:
Department of Mathematics,Wenzhou University, Wenzhou325035, PR China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

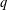We discuss a truncated identity of Euler and present a combinatorial proof of it. We also derive two finite identities as corollaries. As an application, we establish two related 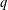$q$-congruences for sums of 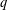$q$-Catalan numbers, one of which has been proved by Tauraso [‘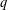$q$-Analogs of some congruences involving Catalan numbers’, Adv. Appl. Math. 48 (2012), 603–614] by a different method.

Keywords

pentagonal number theoremq-congruencesq-Catalan numbers

MSC classification

Primary: 05A19: Combinatorial identities, bijective combinatorics
Secondary: 11A07: Congruences; primitive roots; residue systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 3 , December 2020 , pp. 353 - 359
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the National Natural Science Foundation of China (grant 11801417).

References

Andrews, G. E., The Theory of Partitions (Addison-Wesley, Reading, MA, 1976).Google Scholar
Andrews, G. E. and Merca, M., ‘The truncated pentagonal number theorem’, J. Combin. Theory Ser. A 119 (2012), 1639–1643.10.1016/j.jcta.2012.05.001CrossRefGoogle Scholar
Fürlinger, J. and Hofbauer, J., ‘q-Catalan numbers’, J. Combin. Theory Ser. A 40 (1985), 248–264.CrossRefGoogle Scholar
Gu, C.-Y. and Guo, V. J. W., ‘q-Analogues of two supercongruences of Z.-W. Sun’, Czechoslovak Math. J. to appear.Google Scholar
Guo, V. J. W., ‘Common q-analogues of some different supercongruences’, Results Math. 74 (2019), Article ID 131.10.1007/s00025-019-1056-1CrossRefGoogle Scholar
Guo, V. J. W. and Zeng, J., ‘Multiple extensions of a finite Euler’s pentagonal number theorem and the Lucas formulas’, Discrete Math. 308 (2008), 4069–4078.10.1016/j.disc.2007.07.106CrossRefGoogle Scholar
Guo, V. J. W. and Zudilin, W., ‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358.10.1016/j.aim.2019.02.008CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers (Oxford University Press, Oxford, 1938), 280–286.Google Scholar
Liu, J.-C., ‘Some finite generalizations of Euler’s pentagonal number theorem’, Czechoslovak Math. J. 142 (2017), 525–531.CrossRefGoogle Scholar
Liu, J.-C. and Petrov, F., ‘Congruences on sums of q-binomial coefficients’, Adv. Appl. Math. 116 (2020), Article ID 102003.10.1016/j.aam.2020.102003CrossRefGoogle Scholar
Shanks, D., ‘A short proof of an identity of Euler’, Proc. Amer. Math. Soc. 2 (1951), 747–749.10.1090/S0002-9939-1951-0043808-6CrossRefGoogle Scholar
Tauraso, R., ‘q-Analogs of some congruences involving Catalan numbers’, Adv. Appl. Math. 48 (2012), 603–614.10.1016/j.aam.2011.12.002CrossRefGoogle Scholar