Hostname: page-component-7479d7b7d-pfhbr Total loading time: 0 Render date: 2024-07-15T23:09:35.496Z Has data issue: false hasContentIssue false
  • English
  • Français

Transversals in permutation groups and factorisations of complete graphs

Published online by Cambridge University Press:  17 April 2009

Gil Kaplan  and
Arieh Lev
Gil Kaplan
Affiliation:
Department of Computer Sciences, The Academic College of Tel-Aviv-Yaffo, 4 Antokolsky st., Tel-Aviv, Israel64044
Arieh Lev
Affiliation:
School of Mathematical Sciences, Raymond and Beverly Sacker Faculty of Exact Sciences, Tel-Aviv University, Tel-Aviv, Israel64044
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a transitive permutation group acting on a finite set of order n. We discuss certain types of transversals for a point stabiliser A in G: free transversals and global transversals. We give sufficient conditions for the existence of such transversals, and show the connection between these transversals and combinatorial problems of decomposing the complete directed graph 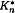into edge disjoint cycles. In particular, we classify all the inner-transitive Oberwolfach factorisations of the complete directed graph. We mention also a connection to Frobenius theorem.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 65 , Issue 2 , April 2002 , pp. 277 - 288
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Alspach, B., ‘The Oberwolfach problem’, in CRC Handbook of Combinatorial Designs, (Colbourn, C.J. and Dinitz, J.H., Editors) (CRC Press, Boca Raton, FL, 1996), pp. 394–395.Google Scholar
[2]Andersen, L. D., ‘Factorizations fo graphs’, in CRC Handbook of Combinatorial Designs, (Colbourn, C.J. and Dinitz, J.H., Editors) (CRC Press, Boca Raton, FL, 1996), pp. 653–667.Google Scholar
[3]Artemovich, O. D., ‘Isolated elements of prime order in finite groups’, Ukrainain Math. J. 40 (1988), 343–345.CrossRefGoogle Scholar
[4]Bertram, E., Herzog, M. and Mann, A., ‘On a graph related to conjugacy classes of groups’, Bull. London Math. Soc. 22 (1990), 569–575.CrossRefGoogle Scholar
[5]Brandl, R., ‘A covering property of finite groups’, Bull. Austral. Math. Soc. 23 (1981), 227–235.CrossRefGoogle Scholar
[6]Cameron, P. J., Permutation groups, London Mathematical Society Student Texts 45 (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
[7]Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., An ATLAS of finite groups. Maximal subgroups and ordinary characters for simple groups (Oxford University press, Eynsham, 1985).Google Scholar
[8]Dixon, J. D. and Mortimer, B., Permutation groups, Graduate Texts in Mathematics 163 (Springer-Verlag, New York, 1996).CrossRefGoogle Scholar
[9]Flavell, P., ‘A note on Frobenius groups’, J. Algebra 228 (2000), 367–376.CrossRefGoogle Scholar
[10]Glauberman, G., ‘Central elements in core free group’, J. Algebra 4 (1966), 402–420.CrossRefGoogle Scholar
[11]Guralnick, R. M., ‘Subgroups of prime power index in a simple group’, J. Algebra 81 (1983), 304–311.CrossRefGoogle Scholar
[12]Kaplan, G., Lev, A. and Roditty, Y., ‘Regular Oberwolfach problems and group sequencing’, J. Combin. Theory Ser. A 96 (2001), 1–19.CrossRefGoogle Scholar
[13]Kleidman, P. and Liebeck, M., The Subgroup structure of the finite classical groups, London Mathematical Soceity Lecture Note Series 129 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
[14]Lev, A. and Roditty, Y., ‘On Hering decomposition of DK n induced by group actions on conjugacy classes’, European J. Combin. 21 (2000), 379–393.CrossRefGoogle Scholar
[15]Stein, A., ‘A Conjugacy class as a transversal in a finite group’, J. Algebra 239 (2001), 365–390.CrossRefGoogle Scholar
[16]Wielandt, H., Finite permutation groups (translated from the German by Bercov, R.), (Academic Press, New York, 1964).Google Scholar