Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-24T17:15:09.106Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSCENDENTAL RUBAN p-ADIC CONTINUED FRACTIONS

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  11 November 2024

GÜLCAN KEKEÇ Open the ORCID record for GÜLCAN KEKEÇ [Opens in a new window]
GÜLCAN KEKEÇ*
Affiliation:
Department of Mathematics, Faculty of Science, Istanbul University, 34134 Vezneciler, Fatih, Istanbul, Turkey
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish explicit constructions of Mahler’s p-adic 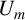$U_{m}$-numbers by using Ruban p-adic continued fraction expansions of algebraic irrational p-adic numbers of degree m.

Keywords

Mahler’s and Koksma’s classifications of transcendental p-adic numbersp-adic U m-numberRuban p-adic continued fractiontranscendence measure

MSC classification

Primary: 11J61: Approximation in non-Archimedean valuations
Secondary: 11J70: Continued fractions and generalizations 11J82: Measures of irrationality and of transcendence
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 13
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alnıaçık, K., ‘On the subclasses ${U}_m$ in Mahler’s classification of the transcendental numbers’, İstanbul Üniv. Fen Fak. Mecm. Ser. A 44 (1979), 39–82.Google Scholar
Alnıaçık, K., ‘On ${U}_m$ -numbers’, Proc. Amer. Math. Soc. 85 (1982), 499–505.Google Scholar
Bugeaud, Y., Approximation by Algebraic Numbers, Cambridge Tracts in Mathematics, 160 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Bugeaud, Y. and Kekeç, G., ‘On Mahler’s classification of $p$ -adic numbers’, Bull. Aust. Math. Soc. 98 (2018), 203–211.CrossRefGoogle Scholar
Bugeaud, Y. and Kekeç, G., ‘On Mahler’s $p$ -adic $S$ -, $T$ -, and $U$ -numbers’, An. Ştiinţ. Univ. Ovidius Constanţa Ser. Mat. 28 (2020), 81–94.Google Scholar
Can, B. and Kekeç, G., ‘On transcendental continued fractions in fields of formal power series over finite fields’, Bull. Aust. Math. Soc. 105 (2022), 392–403.CrossRefGoogle Scholar
İçen, O. Ş., ‘Über die Funktionswerte der $p$ -adisch elliptischen Funktionen I’, İstanbul Üniv. Fen Fak. Mecm. Ser. A 36 (1971), 53–87.Google Scholar
İçen, O. Ş., ‘Anhang zu den Arbeiten “Über die Funktionswerte der $p$ -adisch elliptischen Funktionen I, II”’, İstanbul Üniv. Fen Fak. Mecm. Ser. A 38 (1973), 25–35.Google Scholar
Kekeç, G., ‘On Mahler’s $p$ -adic ${U}_m$ -numbers’, Bull. Aust. Math. Soc. 88 (2013), 44–50.CrossRefGoogle Scholar
Kekeç, G., ‘Some generalized lacunary power series with algebraic coefficients for Mahler’s $U$ -number arguments’, Taiwanese J. Math. 18 (2014), 1–26.CrossRefGoogle Scholar
Kekeç, G., ‘On transcendental regular continued fractions’, Math. Slovaca 73 (2023), 1399–1408.CrossRefGoogle Scholar
Koksma, J. F., ‘Über die Mahlersche Klasseneinteilung der transzendenten Zahlen und die Approximation komplexer Zahlen durch algebraische Zahlen’, Monatsh. Math. Phys. 48 (1939), 176–189.CrossRefGoogle Scholar
Lang, S., ‘Integral points on curves’, Publ. Math. Inst. Hautes Études Sci. 6 (1960), 27–43.CrossRefGoogle Scholar
Laohakosol, V., ‘A characterization of rational numbers by $p$ -adic Ruban continued fractions’, J. Aust. Math. Soc. Ser. A 39 (1985), 300–305.CrossRefGoogle Scholar
Mahler, K., ‘Zur Approximation der Exponentialfunktion und des Logarithmus. I, II’, J. reine angew. Math. 166 (1932), 118–150.CrossRefGoogle Scholar
Mahler, K., ‘Über eine Klasseneinteilung der $p$ -adischen Zahlen’, Mathematica (Leiden) 3 (1935), 177–185.Google Scholar
Ooto, T., ‘Transcendental $p$ -adic continued fractions’, Math. Z. 287 (2017), 1053–1064.CrossRefGoogle Scholar
Pejkovic, T., Polynomial Root Separation and Applications, PhD Thesis (Université de Strasbourg, Strasbourg, 2012).Google Scholar
Perron, O., Irrationalzahlen (Walter de Gruyter, Berlin, 1960).CrossRefGoogle Scholar
Ruban, A. A., ‘Certain metric properties of the $p$ -adic numbers’, Sibirsk. Mat. Ž. 11 (1970), 222–227 (in Russian).Google Scholar
Schlickewei, H. P., ‘ $p$ -adic $T$ -numbers do exist’, Acta Arith. 39 (1981), 181–191.CrossRefGoogle Scholar
Wang, L. X., ‘ $p$ -adic continued fractions I’, Sci. Sinica Ser. A 28 (1985), 1009–1017.Google Scholar
Wang, L. X., ‘ $p$ -adic continued fractions II’, Sci. Sinica Ser. A 28 (1985), 1018–1023.Google Scholar