Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T07:15:02.702Z Has data issue: false hasContentIssue false
  • English
  • Français

Torsion in the additive group of relatively free Lie rings

Published online by Cambridge University Press:  17 April 2009

Vesselin Drensky
Vesselin Drensky
Affiliation:
Institute of Mathematics, Bulgarian Academy of Sciences, 1090 Sofia, P.O. Box 373Bulgaria.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let L = L(X) be the free Lie ring of countable rank and let p be prime. Then L(Vp) = L/[(L')p, L] is the relatively free ring for the variety of Lie rings Vp = [Np−1A, E] and Vp is defined by the identity

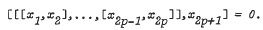
The purpose of this note is to establish that there exist elements of order p in the additive group of L(Vp). Previously, the existence of p-torsion was proved by Kuz'min for p = 2 only. Similar results were obtained for varieties of groups by Gupta when p = 2 and by Stöhr when p = 3.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 33 , Issue 1 , February 1986 , pp. 81 - 87
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Bahturin, J. A.. “Lectures on Lie algebras”, Studien zur Algebra und ihre Anwendungen, 4 (Akademie-verlag, Berlin, 1978).Google Scholar
[2]Gupta, C.K., “The free centre-by-metabelian groups”, J. Austral. Math. Soc. 16 (1973), 294–300.CrossRefGoogle Scholar
[3]Kuz'min, J.V. “Free centre-by-metabelian groups, Lie algebras and D-groups”, Izv. Akad. Nauk SSSR, Ser. Mat. 41 (1977), 3–33. Translation: Math. USSR, Izv. 11 (1977), 1–30.Google Scholar
[4]Latyšev, V.N., “Complexity of nonmatrix varieties of associative algebras. I”, Algebra Logika, 16 (1977), 149–183. Translation: Algebra Logic, 16 (1978), 98–122.Google Scholar
[5]Stöhr, R., “On free central extensions of free nilpotent-by-abelian groups”, Preprint No. 26, Akad. Wiss. DDR, Inst. Math., (1983).Google Scholar
[6]Stöhr, R., “On Gupta representations of central extensions”, Math. Z. 187 (1984), 259–267.CrossRefGoogle Scholar