Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T16:22:56.933Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological entropy for the canonical completely positive maps on graph C*-Algebras

Published online by Cambridge University Press:  17 April 2009

Ja A. Jeong  and
Gi Hyun Park
Ja A. Jeong
Affiliation:
Mathematical Sciences Division, BK21, Seoul National University, Seoul, 151–742, Korea, e-mail: [email protected]
Gi Hyun Park
Affiliation:
Department of Mathematics, Hanshin University, Osan, 447–791, Korea, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let C*(E) = C*(se, pv) be the graph C*-algebra of a directed graph E = (E0, E1) with the vertices E0 and the edges E1. We prove that if E is a finite graph (possibly with sinks) and φE: C*(E) → C*(E) is the canonical completely positive map defined by 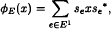then Voiculescu's topological entropy ht(φE) of φE is log r(AE), where r(AE) is the spectral radius of the edge matrix AE of E. This extends the same result known for finite graphs with no sinks. We also consider the map φE when E is a locally finite irreducible infinite graph and prove that 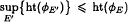, where the supremum is taken over the set of all finite subgraphs of E.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 70 , Issue 1 , August 2004 , pp. 101 - 116
Copyright
Copyright © Australian Mathematical Society 2004

References

[1]Adler, R.L., Konheim, A.G. and McAndrew, M.H., ‘Zoological entropy’, Trans. Amer. Math. Soc. 114 (1965), 309–319.CrossRefGoogle Scholar
[2]Bates, T., Hong, J.H., Raeburn, I. and Szymanski, W., ‘The ideal structure of the C *-algebras of infinite graphs’, Illinois J. Math. 46 (2002), 1159–1176.CrossRefGoogle Scholar
[3]Boca, F.P. and Goldstein, P., ‘Topological entropy for the canonical endomorphism of Cuntz–Krieger algebras’, Bull. London Math. Soc. 32 (2000), 345–352.CrossRefGoogle Scholar
[4]Brown, N.P., ‘Topological entropy in exact C *-algebras’, Math. Annalen 314 (1999), 347–367.CrossRefGoogle Scholar
[5]Choda, M., ‘Endomorphisms of shift type (entropy for endomorphisms of Cuntz algebras)’, in Operator Algebras and Quantum Field Theory (Rome, 1996) (International Press, Cambridge, MA), pp. 469–475.Google Scholar
[6]Cuntz, J. and Krieger, W., ‘A class of C *-algebras and topological Markov chains’, Invent. Math. 56 (1980), 251–268.CrossRefGoogle Scholar
[7]Deaconu, V., ‘Entropy estimates for some C *-endomorphisms’, Proc. Amer. Math. Soc. 127 (1999), 3653–3658.CrossRefGoogle Scholar
[8]Gurevic, B.M., ‘Topological entropy of enumerable Markov chains’, (in Russian), Dokl. Akad. Nauk SSSR 187 (1969), 216–226.Google Scholar
[9]Kirchberg, E., ‘On subalgebras of the CAR-algebra’, J. Funct. Anal. 129 (1995), 35–63.CrossRefGoogle Scholar
[10]Kitchens, B.P., Symbolic dynamics (Springer-Verlag, Berlin, Heidelberg, New York, 1998).CrossRefGoogle Scholar
[11]Kumjian, A., ‘Notes on C *-algebras of graphs’, Contemp. Math. 228 (1998), 189–200.CrossRefGoogle Scholar
[12]Kumjian, A., Pask, D. and Raeburn, I., ‘Cuntz–Krieger algebras of directed graphs’, Pacific J. Math. 184 (1998), 161–174.CrossRefGoogle Scholar
[13]Lind, D. and Marcus, B., An introduction to symbolic dynamics and coding (Cambridge University Press, Cambridge, 1999).Google Scholar
[14]Pinzari, C., Watatani, Y. and Yonetani, K., ‘KMS states, entropy and the variational principle in full C *-dynamical systems’, Comm. Math. Phys. 213 (2000), 331–379.CrossRefGoogle Scholar
[15]Voiculescu, D., ‘Dynamical approximation entropies and topological entropy in operator algebras’, Comm. Math. Phys. 170 (1995), 249–281.CrossRefGoogle Scholar
[16]Walters, P., An introduction to ergodic theory, Graduate Texts in Mathematics 79 (Springer-Verlag, publaddr Berlin, Heidelberg, New York 1982).CrossRefGoogle Scholar