Published online by Cambridge University Press: 13 July 2022
For a positive integer n, let
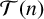 $\mathcal T(n)$
denote the set of all integers greater than or equal to n. A sum of generalised m-gonal numbers g is called tight
$\mathcal T(n)$
denote the set of all integers greater than or equal to n. A sum of generalised m-gonal numbers g is called tight
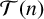 $\mathcal T(n)$
-universal if the set of all nonzero integers represented by g is equal to
$\mathcal T(n)$
-universal if the set of all nonzero integers represented by g is equal to
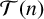 $\mathcal T(n)$
. We prove the existence of a minimal tight
$\mathcal T(n)$
. We prove the existence of a minimal tight
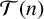 $\mathcal T(n)$
-universality criterion set for a sum of generalised m-gonal numbers for any pair
$\mathcal T(n)$
-universality criterion set for a sum of generalised m-gonal numbers for any pair
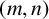 $(m,n)$
. To achieve this, we introduce an algorithm giving all candidates for tight
$(m,n)$
. To achieve this, we introduce an algorithm giving all candidates for tight
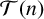 $\mathcal T(n)$
-universal sums of generalised m-gonal numbers. Furthermore, we provide some experimental results on the classification of tight
$\mathcal T(n)$
-universal sums of generalised m-gonal numbers. Furthermore, we provide some experimental results on the classification of tight
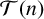 $\mathcal T(n)$
-universal sums of generalised m-gonal numbers.
$\mathcal T(n)$
-universal sums of generalised m-gonal numbers.
The research of the first author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2019R1F1A1064037). The research of the second author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2021R1C1C2010133).