Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T06:08:18.427Z Has data issue: false hasContentIssue false
  • English
  • Français

A theorem on abstract Segal algebras over some commutative Banach algebras

Published online by Cambridge University Press:  17 April 2009

U.B. Tewari  and
K. Parthasarathy
U.B. Tewari
Affiliation:
Department of Mathematics, Indian Institute of Technology, Kanpur 208016 (U.P.), India.
K. Parthasarathy
Affiliation:
Department of Mathematics, University of Calicut, Calicut, India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let B be a commutative, semi-simple, regular, Tauberian Banach algebra with noncompact maximal ideal space Δ(B). Suppose B has the property that there is a constant C such that for every compact subset K of Δ(B) there exists a f ∈ B with 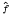= 1 on K, ‖f‖B ≤ C and 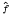has compact support. We prove that if A is a proper abstract Segal algebra over B then for every positive integer n there exists f ∈ B such that fn ∉ A but fn+1 ∈ A. As a consequence of this result we prove that if G is a nondiscrete locally compact abelian group, μ a positive unbounded Radon measure on Γ (the dual group of G), 1 ≤ p < q < ∞ and 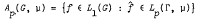, then .

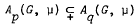Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 25 , Issue 2 , April 1982 , pp. 293 - 301
Copyright
Copyright © Australian Mathematical Society 1982

References

[1]Burnham, J.T., “Closed ideals in subalgebras of Banach algebras. I”, Proc. Amer. Math. Soc. 32 (1972), 551–555.CrossRefGoogle Scholar
[2]Cigler, J., “Normed ideals in L 1(G)”, Nederl. Akad. Wetensch. Proc. Ser. A 72 = Indag. Math. 31 (1969), 273–282.CrossRefGoogle Scholar
[3]Graham, Colin C., “The algebraic radical of a normed ideal in L 1(G)”, Monatsh. Math. 79 (1975), 21–23.CrossRefGoogle Scholar
[4]Kelley, J.L., Namioka, Isaac and Donoghue, W.F. Jr, Lucas, Kenneth R., Pettis, B.J., Poulsen, Ebbe Thue, Price, G. Baley, Robertson, Wendy, Scott, W.R., Smith, Kennan T., Linear topological spaces (Van Nostrand, Princeton, New Jersey; Toronto; London; 1963. Second printing: Graduate Texts in Mathematics, 36. Springer-Verlag, New York, Heidelberg, Berlin, 1976).CrossRefGoogle Scholar
[5]Larsen, Ronald, An introduction to the theory of multipliers (Die Grundlehren der mathematischen Wissenschaften, 175. Springer-Verlag, Berlin, Heidelberg, New York, 1970).Google Scholar
[6]Larsen, Ronald, “The multipliers for functions with Fourier transforms in Lp”, Math. Scand. 28 (1971), 215–225.CrossRefGoogle Scholar
[7]Larsen, Ron, Liu, Teng-sun, and Wang, Ju-kwei, “On functions with Fourier transforms in Lp”, Michigan Math. J. 11 (1964), 369–378.CrossRefGoogle Scholar
[8]Loomis, Lynn H., An introduction to abstract harmonic analysis (Van Nostrand, New York, Toronto, London, 1953).Google Scholar
[9]Reiter, Hans, Classical harmonic analysis and locally compact groups (Clarendon Press, Oxford, 1968).Google Scholar
[10]Reiter, Hans, L1-algebras and Segal algebras (Lecture Notes in Mathematics, 231. Springer-Verlag, Berlin, Heidelberg, New York, 1971).CrossRefGoogle Scholar
[11]Tewari, U.B. and Gupta, A.K., “The algebra of functions with Fourier transforms in a given function space”, Bull. Austral. Math. Soc. 9 (1973), 73–82.CrossRefGoogle Scholar