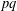Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rodtes, Kijti
and
Chimla, Kunlathida
2018.
Symmetry classes of tensors and semi-direct product of finite abelian groups.
Linear and Multilinear Algebra,
Vol. 66,
Issue. 11,
p.
2191.