Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gerhold, Stefan
and
Gülüm, I. Cetin
2019.
Peacocks nearby: Approximating sequences of measures.
Stochastic Processes and their Applications,
Vol. 129,
Issue. 7,
p.
2406.


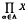
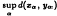 , is the sup metric on
, is the sup metric on 